
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический образ уравнения состояния.Содержание книги
Поиск на нашем сайте
Ранее указывалось, что состояние системы однозначно определяется уравнением состояния вида Однако на практике нет необходимости всегда пользоваться трехмерным пространством для определения состояния системы, достаточно установить только два параметра, так как третий определится из уравнения состояния. Другими словами, для однозначного определения состояния системы достаточно определить положение фигуративной точки в двухмерной системе координат, например Р - Т или Т - С. Такое графическое изображение уравнения состояния системы носит название диаграммы состояния. Важно заметить, что, несмотря на широкое использование в термодинамике уравнений состояния, они весьма приближенны, а все попытки их уточнения приводят к громозким формулам, работа с которыми затруднительна. Поэтому диаграммы состояния приобретают огромный интерес. С их помощью, используя экспериментальные данные, открывается возможность доступно и наглядно изображать в виде геометрических образов реальную взаимосвязь термодинамических параметров, определяющих состояние системы.
Однокомпонентные системы. Примером онокомпонентной системы является любое вещество (элемент или химическое соединение), обладающее строго определенным химическим составом во всех агрегатных состояниях. Из уравнения состояния
Кривые ОМ, ОN и ОQ делят координатное поле на три области. Каждая из них обозначает определенное агрегатное состояние воды: S - область соответствует твердому (кристаллическому) состоянию; L - область соответствует жидкому состоянию; G - область соответствует газообразному состоянию; Для любой точки, лежащей внутри той или иной области правило фаз определяет: c = k - f + 2 = 1 - 1 + 2 = 2, т. е. система обладает двумя степенями свободы. Это означает, что одновременно изменение давления и температуры в пределах данной области не вызовет нарушения фазового равновесия. Линия ON - геометрическое место точек, определяющих значения Р и Т, которые обеспечивают равновесное сосуществование двух фаз - жидкости и пара:
Одновременно эта кривая выражает зависимость давления насыщенного пара от температуры или зависимость температуры кипения жидкости от давления. В этой связи кривая ON называется кривой испарения. Линия ОМ - граница между областью S и областью L, представляющая собой совокупность точек, соответствующих состоянию двухфазного равновесия между твердой и жидкой фазами:
Линия ОМ называется кривой плавления, так как она изображает зависимость температуры плавления льда от давления.
Линия ОQ - кривая возгонки или сублимации. Точки на этой кривой соответствуют состоянию равновесия твердой и газообразной фаз:
Эта линия устанавливает зависимость давления пара над твердой фазой от температуры и, с другой стороны, устанавливает влияние давления на температуру возгонки. В соответствии с уравнением правила фаз, число степеней свободы для любой точки на любой кривой составит: c = k - f + 2 = 1 - 2 + 2 = 1, то есть система обладает одной степенью свободы. Это означает, что не нарушая состояния равновесия, можно произвольно изменять только один параметр. При этом другой параметр тоже должен изменяться в соответствии с уравнением соответствующей кривой. Линии ON, OM и OQ имеют одну общую точку, точку О, называемую тройной точкой. Она определяет значения параметров, при которых жидкость, пар и кристаллы находятся в состоянии равновесия. По правилу фаз число степеней свободы системы в тройной точке: c = k - f + 2 = 1 - 3 + 2 = 0, что определяет условия равновесного сосуществования трех фаз при строго фиксированных значениях Р и Т. Для воды: Р0 = 0,006
Двухкомпонентные системы. Двухкомпонентными называются системы, образованные двумя компонентами, которые могут быть как простыми веществами, так и химическими соединениями. Соотношение компонентов способно значительно изменять свойства системы. Исходя из принципов построения уравнения состояния для двухкомпонентной системы справедливо уравнение:
где С1, С2 - концентрации первого и второго компонентов. Но С1 + С2 = const и если р = const, то (6.3) упрощается:
Таким образом, диаграмма состояния двухкомпонентной системы строится в координатах Т - С. Если в однокомпонентной системе энергия Гиббса фазы изменяется только при изменении Р и Т в соответствии с уравнением (4.67) в двухкомпонентной системе энергия Гиббса определяется не только значениями Р и Т, но и составом фаз, поэтому
где ni - количество i-го компонента в фазе. Уравнение (6.5) - главное уравнение химической термодинамики, основа применения
термодинамики в химии и теории фазовых переходов. Системы, поведение которых описывается на основе (6.5) называются открытыми (незамкнутыми). Любая точка на диаграмме двухкомпонентной системы - носитель определенной информации (рис. 6.3). Так фигуративная точка (а) указывает на то, что сплав состава (%В, %А) находится при температуре ТА. Сплавом называют твердые или жидкие системы, образованные, главным образом, сплавлением двух или более металлов, а также металлов с различными неметаллами. На диаграмму двухкомпонентной системы наносят только точки, характеризующие процессы плавления или затвердевания, фазовые переходы и т.п. Линии, соединяющие эти точки, носят определенные названия. Линия, являющая собой совокупность точек начала кристаллизации всех сплавов системы, называется линией ликвидус. Линия, представляющая собой совокупность точек конца кристаллизации, носит название линии солидус.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.120.112 (0.009 с.) |

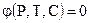 . В то же время численные значения параметров конкретного состояния определяют положение некоторой точки (фигуративной точки) в трехмерной системе координат Р - Т -С (рис. 6.1).
. В то же время численные значения параметров конкретного состояния определяют положение некоторой точки (фигуративной точки) в трехмерной системе координат Р - Т -С (рис. 6.1).
 .
.
 .
.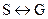 .
. 105 Па и Т0 = 273,0075 К.
105 Па и Т0 = 273,0075 К.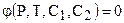 , (6.3)
, (6.3) . (6.4)
. (6.4)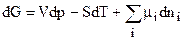 , (6.5)
, (6.5)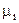 - химический потенциал i-го компонента;
- химический потенциал i-го компонента;



