
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава I. Химическая термодинамикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введение В настоящее время физическая химия - самостоятельная дисциплина, имеющая огромное значение для ряда смежных как теоретических, так и прикладных дисциплин. "Физическая химия - наука, изучающая на основе положений и опытов физических, причину того, что происходит через химические операции в сложных телах", - так определил суть предмета великий русский ученый М. В. Ломоносов. Им же впервые в 1752 г. Был прочитан курс лекций по физической химии но лишь в 1860 г. профессором Бекетовым Н. Н. в ХГУ было введено преподавание курса физической химии. С этого времени, т. е. со II половины XIX века физическая химия начинает складываться как наука трудами русских, советских и зарубежных ученых. Содержание курса физической химии обычно делят на несколько основных разделов, характеризующих направления этой науки и ее содержание. Основные разделы физической химии таковы: - строение вещества; - химическая термодинамика; - растворы; - электрохимия; - химическая кинетика; - поверхностные явления; - колоидные растворы. Это деление условно, т. к. реальный процесс обычно представлен несколькими явлениями. Физическая химия пользуется, главным образом, тремя методами теоретического обобщения и лишь их совместное использование дает достаточно полное решение задачи. Это следующие методы: - статистический, в основе которого лежит наука статистическая физика; - термодинамический, являющийся выражением суммарного результата статистических закономерностей; - квантово-механический, объясняющий ряд основных явлений физической химии, которые оставались непонятыми. Типичными проблемами физической химии являются: - проблема химического равновесия, решение задач в рамках которой позволяет установить условия максимально полного разрешения химической реакции; - проблема скорости химической реакции, решение которой позволяет обеспечивать высокую производительность технологических процессов; - проблема химической связи, в рамках которой появляются сведения о внутреннем устройстве молекул, атомов и их реакционной способности; - проблема связи свойств веществ с их структурой и химическим составом, обсуждение которой позволяет прогнозировать получение материалов с заданным уровнем служебных характеристик. Теплоемкость идеального газа. Из молекулярно-кинетической теории следует, что кинетическая энергия (WК) 1 моля идеального газа равна:
где NA - число Авогадро, равное 6,02 1023 Дж/К. Учитывая, что
Используя соотношение (2.8):
Уравнения (2.11) и (2.12) представляют закон Дюлонга - Пти для идеальногогаза. Если идеальный газ одноатомный, то i = 3 и тогда:
Для двухатомного газа i = 5 и тогда:
В случае трехатомного газа i = 6, поэтому: СV = 3R; СР = 4R. (2.15)
Теплоемкость твердых тел. Твердое тело можно представить в виде огромной молекулы, состоящей из отдельных атомов. Число атомов в 1 моле равно NA, тогда общее число степеней свободы – 3 NA и выражение для расчета теплоемкости принимает следующий вид:
причем СV Соотношение (2.16) – закон Дюлонга – Пти для твердых тел. Оказалось, что для углерода, кремния и бора соотношение (2.16) не выполняется. Кроме того закон Дюлонга – Пти не учитывает температурную зависимость теплоемкости.
Правило Неймана - Коппа. Из многочисленных эмпирических соотношений предлагавшихся для вычисления теплоемкостей твердых тел, наибольшее распространение имеет правило Неймана - Коппа, известное еще как правило аддитивности теплоемкости. Это правило, сформулированное Нейманом в 1831 г. и Коппом в 1864 г., позволяет приблизительно вычислять теплоемкость химических соединений. Согласно этому правилу, молярная теплоемкость химических соединений в твердом состоянии равна сумме молярных теплоемкостей элементов, входящих в это соединение. Принимая во внимание правило Дюлонга - Пти, для соединения, состоящего из N атомов справедливо соотношение: C = N(3R). (2.17) Для приближенной оценки удельной теплоемкости сплава используется соотношение вида: С = рС1 + qС2 + …, (2.18) где С - удельная теплоемкость сплава; р, q - массовые доли компонентов сплава; С1, С2 - удельные теплоемкости компонентов сплава.
Закон Гесса. В основе термохимии лежит закон, согласно которому тепловой эффект реакции не зависит от пути этой реакции, а определяется видом и состоянием исходных и конечных продуктов реакции. Гесс Герман Иванович (1802 – 1850 г. г.) – русский химик, академик Петербуржской Академии наук. Существо закона вытекает из уравнения первого начала термодинамики: QV = - U и Н – функции состояния, поэтому QV и QP также функции состояния системы. Иллюстрация закона Гесса. C + O2 = CO2 + Q1, (3.13) есть первый вариант реакции в системе. C + CО + второй возможный вариант реакции. Так из одинакового исходного состояния образуется одинаковое для рассмотренных вариантов конечное состояние, то: Q1 = Q2 + Q3. (3.15) Закон Гесса имеет огромное практическое значение. С его помощью устанавливаются значения тепловых эффектов реакций, экспериментальное определение которых затруднительно. Для этих целей широко используются следствия из закона Гесса.
Следствия из закона Гесса. I следствие. Тепловой эффект реакции разложения какого-либо химического соединения равен по абсолютной величине, но противоположен по знаку тепловому эффекту реакции образования этого соединения. II следствие. Если совершаются две реакции, приводящие из различных исходных состояний к одинаковым конечным, то разница между тепловыми эффектами реакций представляет собой тепловой эффект перехода из одного исходного состояния в другое. III следствие. Если совершаются две реакции, приводящие из одинаковых исходных состояний к различным конечным, то разница их тепловых эффектов есть тепловой эффект реакции перехода из одного конечного состояния в другое. IV следствие. Тепловой эффект химической реакции равен сумме теплот образования конечных и исходных продуктов реакции с учетом коэффициентов перед химическими формулами этих продуктов в уравнении химической реакции. В аналитической форме записи:
где Q – тепловой эффект химической реакции;
Теплота образования – тепловой эффект химической реакции образования данного вещества (продукта химической реакции) из простых, устойчивых в данных условиях. Стандартной теплотой образования называют теплоту образования, отнесенную к температуре 298 К и давлению 1,01 * 105 Па. Если известна эта величина, то термохимический расчет позволяет определить теплоту образования и при других значениях параметров состояния. V следствие. Тепловой эффект химической реакции равен разности сумм теплот сгорания исходных и конечных продуктов химической реакции с учетом коэффициентов у химических формул этих веществ в уравнении химической реакции. В аналитической форме записи:
где Теплота сгорания – тепловой эффект реакции сгорания 1 моля вещества в атмосфере чистого кислорода до образования высшего оксида. Теплота сгорания существенно зависит от температуры, поэтому для термохимических расчетов вводится некоторая точка отсчета – стандартная теплота сгорания. Стандартной теплотой сгорания называется теплота сгорания, отнесенная к стандартным условиям, т. е. к 298 К и р = 1,01*105 Па. VI следствие. Теплота растворения. Теплотой растворения называется количество теплоты, выделяемое или поглощаемое при растворении 1 моля вещества в таком количестве растворителя, при котором его дальнейшее добавление к раствору уже не вызывает изменение температуры последнего. В этой связи табличные значения теплот относятся к раствору 1 моля растворяемого вещества в 200 – 400 молях растворителя. Теплота растворения (q) – сумма двух слагаемых: q = q1 + q2, (3.18) где q1 – теплота, затрачиваемая на перевод вещества из обычного состояния в то, в котором оно находится в растворе; q2 – теплота взаимодействия частиц растворителя с частицами растворенного вещества (теплота сольватации или гидратации, если растворитель вода). VII следствие. Теплота плавления и испарения. Процессы плавления и испарения всегда эндотермические процессы, т. к. на их реализацию необходимо затратить значительную энергию на разрушение данного порядка в структуре вещества. Между теплотой испарения (
определяемая как правило Трутона. Существует такая же взаимосвязь для теплоты плавления (
называемая правилом Ричардса. VIII следствие. Теплота нейтрализации. Реакция нейтрализации – реакция между щелочами и кислотами. В ее основе лежит процесс нейтрализации ионов водорода (Н+) ионами гидроксида (ОН-), приводящий к образованию молекул воды. Следовательно, тепловой эффект всех подобных реакций должен быть одинаков, что и показали точные опыты. Теплота нейтрализации примерно равна 57,08 кДж/моль, если в реакции участвует одноосновная кислота
Содержание второго начала термодинамики. Первого начала термодинамики недостаточно для полной характеристики термодинамических процессов. В рамках первого начала можно установить энергетический баланс процессов, но получить сведения о возможности, направлении и пределах их протекания не представляется возможным. Итак, второе начало позволяет: - находить направление и устанавливать возможность самопроизвольного (естественного, спонтанного) течения термодинамических процессов и пределы их протекания; определять условия, при которых превращение какого-либо запаса энергии в полезную работу происходит наиболее полно. Предлагаются следующие формулировки второго начала термодинамики: “... холодное тело В, погруженное в теплое тело А, не может воспринять большую степень теплоты, чем какую имеет А.” (М. В. Ломоносов) “... невозможен процесс, единственный результат которого состоял бы в переходе энергии от более холодного тела к более горячему.” (Рудольф Клаузиус) “... невозможен процесс, единственный результат которого состоял бы в поглощении теплоты от нагревателя и полного преобразования этой теплоты в работу.” (У. Томсон (лорд Кельвин)) Вычисление энтропии. В качестве отправной точки необходимо воспользоваться соотношением (4.21). Тогда для изотермического процесса (Т = const):
где dq = dU + pdV, а dU = 0, поэтому
Из уравнения состояния идеального газа:
если n = 1 моль, следовательно:
После интегрирования:
Для случая P = const:
где dqP = CPdT, поэтому
и после интегрирования:
Если СР = const, то
По аналогии для случая V = const:
и если СV = const, то
Если изотермическое превращение является фазовым - плавление, испарение, сублимация или полиморфный переход, то:
где q - энергетический эффект фазового перехода; Т - температура фазового перехода. Таким образом, рассмотрены некоторые уравнения, позволяющие вычислять изменение энтропии, если известны изменения параметров системы и ее теплоемкость. Существуют и другие методы определения изменения энтропии, например по измерениям электродвижущих сил гальванических элементов, о чем речь пойдет в главе “Электрохимия”.
Химическое равновесие. Химическое сродство. Для реакции (4.87) ход рассуждений, использованный в параграфе 12 в условиях V, T=const дает:
или сокращенно
где которой умножено на соответствующий коэффициент. Замена концентраций парциальными давлениями дает в условиях P, T = const:
Уравнения (4.92) и (4.93) - уравнения изотермы химической реакции или уравнения Вант-Гоффа. Способность различных веществ взаимодействовать между собой с образованием новых веществ была замечена давно и получила наименование химического сродства. Критерий оценки химического сродства был найден не сразу. Несостоятельным оказалось предположение о равенстве теплового эффекта реакции и сродства. Голландский физико - химик Вант-Гофф предложил новую теорию химического сродства, которая, не объясняя его природу, дает возможность количественно оценить его: в качестве мерила химического сродства предложено использовать полную максимальную работу реакции, если реакция протекает при V = const:
или максимальную полезную работу, если реакция протекает в условиях p = const:
где значения AV и AP могут быть рассчитаны и по уравнениям изотермы химической реакции (4.94). Для того, чтобы иметь возможность сравнивать сродство различных веществ, было введено понятие нормального (стандартного) сродства. К уравнению нормального сродства легко подойти, если начальные парциальные давления или концентрации реагентов равны единице. Тогда:
Сравнивая Замечание. Для растворов правильнее пользоваться не молярными концентрациями (Сi) в случае расчета химического сродства, а мольными долями компонентов.
От температуры и давления. Полученные сведения о равновесии можно дополнить, установив зависимость константы равновесия от температуры и давления. Дифференцирование уравнения (4.93) по температуре дает:
Полученное выражение и значение АР из уравнения (4.93) необходимо ввести в уравнение Гиббса - Гельмгольца:
и получить
откуда после упрощений:
По аналогии:
Или, учитывая соотношения
Полученные уравнения вида (4.95) и (4.96) - это уравнения изобары и изохоры химической реакции, устанавливающие зависимость константы равновесия химической реакции от температуры. Интегрирование уравнений (4.95) и (4.96) в обобщенной форме их записи позволяет получить точное решение в виде:
Если предположить, что Q
Из (4.98) видно, что Сделанные выводы представляют собой частный случай принципа Ле-Шателье (или принцип подвижного равновесия), который позволяет в простейших случаях предвидеть направление течения химической реакции. Согласно этому принципу, изменение внешних условий (Т и Р) термодинамической равновесной системы вызывает в ней процессы, противодействующие произвольному изменению. Например для реакций вида: N2 + O2 2NО + O2 повышение температуры сдвинет первое равновесие в сторону образования NO, а второе равновесие - в сторону диссоциации NО2. Константа равновесия kP пропорциональна функции
Но это вовсе не означает, что при изменении давления количество веществ, находящихся в равновесии не изменяется. Поэтому изменение давления влияет на kN реакции. Из уравнения (4.90):
и затем:
Отсюда после дифференцирования при постоянной температуре:
Используя уравнение состояния идеального газа PV = nRT и считая Р и Т постоянными: Р
называемое уравнением Планка. Если химическая реакция сопровождается уменьшением количества вещества (
Термическая диссоциация. Многие вещества, нагревом переведенные в газообразное состояние при последующем повышении температуры разлагаются, причем степень их разложения увеличивается с повышением температуры, например: I2 Количественно состояние диссоциирующего вещества характеризуется степенью диссоциации ( Отношение общего числа частиц после диссоциации к числу молекул до диссоциации называется коэффициентом диссоциации (i). Для установления связи Следовательно величина i определяется:
или
Таким образом I2 PCl5 2NO2 С другой стороны, значение коэффициента диссоциации рассчитывается из соотношения:
где М - теоретическая молекулярная масса вещества;
Таким образом, по аномалии молекулярной массы можно определять коэффициент диссоциации, что позволяет определить значение константы равновесия реакции диссоциации. Но при этом следует учитывать, что в каждом кокретном случае связь константы равновесия и степени диссоциации будет различной. Наиболее простой случай диссоциации: Cl2 n 0 0 - начальные количества вещества n - n Сумма количеств молей реагентов в состоянии равновесия:
Тогда значения равновесных парциальных давлений реагентов в состоянии равновесия:
откуда
В случае диссоциации водяного пара: 2Н2О = 2Н2 + О2 n 0 0 - начальные количества вещества n - n Общее количество вещества в равновесии:
Тогда парциальные давления Н2О, Н2 и О2 составят:
Поэтому:
если Тепловая теорема Нернста. Обобщенное уравнение Гиббса - Гельмгольца в дифференциальной форме записи имеет вид (4.42):
После умножения правой и левой его частей на
или
После интегрирования:
или в более удобной форме записи:
Урвнение (5.4) - интегральная форма записи уравнения Гиббса - Гельмгольца.
Для выбора правильной А - кривой достаточно найти одно значение А1 при какой-либо Т1, отличной от нуля. Это тот эмпирический путь, условия реализации которого были описаны ранее. Теорема Нернста позволяет сделать правильный выбор более общим способом. Им было установлено на основании многочисленных экспериментальных данных, что в конденсированных системах Q - кривая и А - кривая сливаются вблизи абсолютного нуля температуры (тепловая теорема Нерста).
Конденсированными называются системы, состоящие из чистых совершенно однородных твердых кристаллических тел, не образующих между собой растворов. Для дальнейшего использования теоремы Нернста ее необходимо выразить в аналитической форме. Слияние двух кривых определяется слиянием их касательных, т. е. равенством пределов их производных при Т
Для отыскания значения общего предела производных, следует вновь обратиться к уравнению Гиббса - Гельмгольца, переписанному в виде:
При Т0 = 0 выражение (5.6) обращается в неопределенность, так как А0 = Q0 и
Знаменатель этого выражения равен единице, а числитель, согласно (5.5), обращается в ноль. Поэтому:
и согласно тому же (5.5):
Итак, общая касательная кривых Q и А = f (T) параллельна температурной оси (рис. 5.1), что и определяет правильность выбора А = f (T) - кривой. В дальнейшем теорема Нернста была обоснована более строгим образом, независимо от принципа максимальной работы. Кроме того, было также показано, что жидкости не следует причислять к конденсированным телам, к которым теорема Нернста точно применима.
Глава VI. Правило фаз. Иллюстрацией практического применения второго закона термодинамики является правило фаз Гиббса (1878 г.), дающее качественную характеристику гетерогенных многофазных равновесных систем. Это правило получило многочисленные подтверждения и разнообразные применения.
1. Основные понятия и определения. Термодинамические системы, представленные телом или группой тел, изолированными от окружающей среды и пребывающие в непрерывном движении бывают гомо- и гетерогенными. Гомогенные системы - системы, внутри которых отсутствуют поверхности раздела, отделяющие друг от друга части системы, отличающиеся свойствами. Гетерогенные системы имеют внутри себя границы раздела, отделяющие части системы, отличающиеся свойствами. Ранее указывалось, что состояние системы определяется совокупностью параметров состояния (Р, Т, V). Фаза (f) - состояние материи, которое повсюду однородно не только по химическому составу, но и по физическим свойствам, - такое определение этому понятию дал Д. У. Гиббс. Фазы бывают твердыми, жидкими и газообразными. Составная часть системы (р) - химически индивидуальные вещества, представляющие систему и способные к самостоятельному существованию вне системы. Например система, образованная тремя химическими соединениями NH4Cl(ТВ), NH3(Г) и НCl(Г) состоит из трех составных частей. Компонент системы (k) - химические индивидуумы, наименьшее число которых необходимо и достаточно для образования всех фаз данной системы. Число компонентов равно числу составных частей за вычетом числа уравнений (r), связывающих составные части. В рассматриваемой системе. состоящей из трех составных частей, возможна реакция вида: NH4Cl(ТВ) поэтому число компонентов будет равно двум: k = p - r = 3 - 1 = 2. Числом степеней свободы (с) называется число независимых термодинамических параметров, определяющих состояние системы. Независимыми являются те параметры, которые можно произвольно задавать или изменять без того,чтобы это влекло за собой изменение других независимых параметров состояния, причем при изменении независимых параметров состояния число фаз в системе не должно изменяться. Чтобы рассчитать число степеней свободы системы нужно из общего числа параметров состояния вычесть число связывающих их уравнений.
Уравнение правила фаз. Пусть рассматриваемая система состоит из f - фаз и k - компонентов, причем каждый из k - компонентов находится в каком-то количестве в каждой из f - фаз. Давление и температура одинаковы для всех фаз данной системы, т.е. имеется два общих параметра состояния. Так как каждый компонент находится в каждой фазе, то возможные концентрации компонентов во всех фазах:
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Число возможных концентраций компонентов составит величину k Для каждой из фаз имеется свое уравнение состояния. Например, для первой фазы это уравнение таково:
Таких уравнений столько, сколько фаз в системе, т.е. f - штук. Система находится в состоянии термодинамического равновесия, что означает равенство химических потенциалов компонентов (
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Число строк в матрице равно числу компонентов (k), а число столбцов равно (f - 1), тогда общее число уравнений составит: k(f - 1). Таким образом, общее число уравнений, связывающих значения химических потенциалов компонентов вычислится как f + k(f - 1). Согласно определению, число степеней свободы равно разности между общим числом параметров состояния и числом уравнений, связывающих эти параметры: с = (k или с = k - f + 2. (6.4) т. е. число степеней свободы равно разности между числом компонентов и фаз плюс два. В системах без участия в равновесии газообразной фазы, один из параметров, общий для всех фаз системы, а именно давление, не оказывает влияние на равновесие в системе, если изменяется в небольших пределах и поэтому исключается из числа общих параметров состояния. Это положение применимо, в частности, к металлическим расплавам и поэтому уравнение правила фаз записывается в виде: с = k - f + 1. (6.5) Равновесие нонвариантно (безвариантно), если с = 0, моновариантно (одновариантно), если с = 1 и дивариантно (двухвариантно), если с = 2.
Однокомпонентные системы. Примером онокомпонентной системы является любое вещество (элемент или химическое соединение), обладающее строго определенным химическим составом во всех агрегатных состояниях. Из уравнения состояния
Кривые ОМ, ОN и ОQ делят координатное поле на три области. Каждая из них обозначает определенное агрегатное состояние воды: S - область соответствует твердому (кристаллическому) состоянию; L - область соответствует жидкому состоянию; G - область соответствует газообразному состоянию; Для любой точки, лежащей внутри той или иной области правило фаз определяет: c = k - f + 2 = 1 - 1 + 2 = 2, т. е. система обладает двумя степенями свободы. Это означает, что одновременно изменение давления и температуры в пределах данной области не вызовет нарушения фазового равновесия. Линия ON - геометрическое место точек, определяющих значения Р и Т, которые обеспечивают равновесное сосуществование двух фаз - жидкости и пара:
Одновременно эта кривая выражает зависимость давления насыщенного пара от температуры или зависимость температуры кипения жидкости от давления. В этой связи кривая ON называется кривой испарения. Линия ОМ - граница между областью S и областью L, представляющая собой совокупность точек, соответствующих состоянию двухфазного равновесия между твердой и жидкой фазами:
Линия ОМ называется кривой плавления, так как она изображает зависимость температуры плавления льда от давления.
Линия ОQ - кривая возгонки или сублимации. Точки на этой кривой соответствуют состоянию равновесия твердой и газообразной фаз:
Эта линия устанавливает зависимость давления пара над твердой фазой от температуры и, с другой стороны, устанавливает влияние давления на температуру возгонки. В соответствии с уравнением правила фаз, число степеней свободы для любой точки на любой кривой составит: c = k - f + 2 = 1 - 2 + 2 = 1, то есть система обладает одной степенью свободы. Это означает, что не нарушая состояния равновесия, можно произвольно изменять только один параметр. При этом другой параметр тоже дол
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 635; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.143 (0.016 с.) |

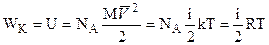 , (2.10)
, (2.10) можно получить:
можно получить: . (2.11)
. (2.11) . (2.12)
. (2.12) . (2.13)
. (2.13) . (2.14)
. (2.14) , (2.16)
, (2.16) СР.
СР. V, а QP = -
V, а QP = -  O2 = CO + Q2,
O2 = CO + Q2, , (3.16)
, (3.16) - теплоты образования конечных и исходных продуктов реакции соответственно.
- теплоты образования конечных и исходных продуктов реакции соответственно. , (3.17)
, (3.17) - теплоты сгорания конечных и исходных продуктов реакции соответственно.
- теплоты сгорания конечных и исходных продуктов реакции соответственно. ) и температурой кипения (ТЕ) существует взаимосвязь:
) и температурой кипения (ТЕ) существует взаимосвязь: , (3.19)
, (3.19) ) и температуры плавления (TS):
) и температуры плавления (TS): , (3.20)
, (3.20) ,
, . (4.39)
. (4.39) , (4.40)
, (4.40) . (4.41)
. (4.41)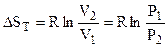 . (4.42)
. (4.42) ,
,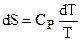
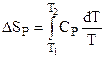 . (4.43)
. (4.43)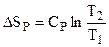 . (4.44)
. (4.44)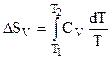 . (4.45)
. (4.45) . (4.46)
. (4.46)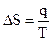 , (4.47)
, (4.47) (4.91)
(4.91)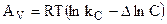 , (4.92)
, (4.92) - алгебраическая сумма логарифмов начальных концентраций, каждое из слагаемых
- алгебраическая сумма логарифмов начальных концентраций, каждое из слагаемых . (4.93)
. (4.93)

 и
и . (4.95)
. (4.95) или
или  различных веществ, получают характеристику удаленности данной системы от состояния равновесия.
различных веществ, получают характеристику удаленности данной системы от состояния равновесия. . (4.94)
. (4.94)
 ,
,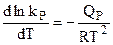 . (4.95)
. (4.95) . (4.96)
. (4.96) и
и  :
: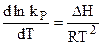 и
и 
 . (4.97)
. (4.97) f (T), то решение уравнений (4.95) и (4.96) выглядит:
f (T), то решение уравнений (4.95) и (4.96) выглядит: . (4.98)
. (4.98) , причем, если Q > 0 (экзотермическая реакция), то с ростом температуры значение k уменьшается, а если Q < 0 (эндотермическая реакция), то при увеличении температуры величина k, наоборот, увеличивается.
, причем, если Q > 0 (экзотермическая реакция), то с ростом температуры значение k уменьшается, а если Q < 0 (эндотермическая реакция), то при увеличении температуры величина k, наоборот, увеличивается. 2NO - 180,0 кДж,
2NO - 180,0 кДж, , но стандартная функция энергия Гиббса определяется при строго фиксированном давлении. Следовательно, некорректно обсуждать изменение kP при изменении давления для случая идеальных газов. Таким образом при постоянной температуре:
, но стандартная функция энергия Гиббса определяется при строго фиксированном давлении. Следовательно, некорректно обсуждать изменение kP при изменении давления для случая идеальных газов. Таким образом при постоянной температуре: . (4.99)
. (4.99)
 .
.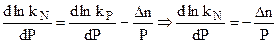 .
. в полученное уравнение kN = f (P), можно получить уравнение:
в полученное уравнение kN = f (P), можно получить уравнение: , (4.100)
, (4.100) , и с увеличением давления в системе равновесие смещается в сторону конечных продуктов химической реакции, что обеспечивает большую полноту превращения исходных продуктов химической реакции в конечные.
, и с увеличением давления в системе равновесие смещается в сторону конечных продуктов химической реакции, что обеспечивает большую полноту превращения исходных продуктов химической реакции в конечные. ), которая представляет собой отношение числа распавшихся молекул к числу молекул до распада. Очевидно, что 0
), которая представляет собой отношение числа распавшихся молекул к числу молекул до распада. Очевидно, что 0  1.
1.
 . (4.101)
. (4.101) , причем m может принимать различные значения в зависимости от вида химической реакции, например:
, причем m может принимать различные значения в зависимости от вида химической реакции, например: , (4.102)
, (4.102) - опытная молекулярная масса вещества (она меньше теоретической по причине диссоциации вещества).
- опытная молекулярная масса вещества (она меньше теоретической по причине диссоциации вещества). .
. ,
, ,
, .
. n
n 
 ,
, ,
, .
. ,
, .
. :
:
 . (5.3)
. (5.3)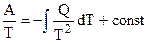
 . (5.4)
. (5.4) Уравнение (5.4) неоднозначно, т. к. в него входит const, значение которой ничем не ограничено. Поэтому в координатном поле “энергия - температура”, вместо одной кривой А = f (T), получается семейство кривых, отличающихся значением const. В то же время зависимость Q= f (T) однозначна и представлена единственной кривой (рис. 5.1).
Уравнение (5.4) неоднозначно, т. к. в него входит const, значение которой ничем не ограничено. Поэтому в координатном поле “энергия - температура”, вместо одной кривой А = f (T), получается семейство кривых, отличающихся значением const. В то же время зависимость Q= f (T) однозначна и представлена единственной кривой (рис. 5.1). 0 и значений функций:
0 и значений функций: и А0 = Q0. (5.5)
и А0 = Q0. (5.5) . (5.6)
. (5.6) . Для ее раскрытия необходимо найти отношение пределов производных от числителя и знаменателя:
. Для ее раскрытия необходимо найти отношение пределов производных от числителя и знаменателя: .
. (5.7)
(5.7) (5.8)
(5.8) - для первого компонента;
- для первого компонента; - для второго компонента;
- для второго компонента; - для k - го компонента. (6.1)
- для k - го компонента. (6.1) f. Итого, для рассматриваемой системы общее число параметров состояния равно (k
f. Итого, для рассматриваемой системы общее число параметров состояния равно (k  . (6.2)
. (6.2)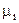 ) во всех фазах системы, т.е.:
) во всех фазах системы, т.е.: - для первого компонента;
- для первого компонента; - для второго компонента;
- для второго компонента; - для k - го компонента. (6.3)
- для k - го компонента. (6.3)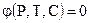 следует, что при с = const, диаграмма состояния однокомпонентной системы строится на плоскости в системе координат Р - Т. Наиболее часто как пример диаграммы однокомпонентной системы приводится диаграмма состояния воды в области невысоких давлений (рис.6.2).
следует, что при с = const, диаграмма состояния однокомпонентной системы строится на плоскости в системе координат Р - Т. Наиболее часто как пример диаграммы однокомпонентной системы приводится диаграмма состояния воды в области невысоких давлений (рис.6.2). .
.
 .
.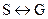 .
.


