
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Химическая термодинамика.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теоретические сведения Химический процесс можно рассматривать как первую ступень при восхождении от химических объектов – электрон, протон, атом – к живой системе. Учение о химических процессах – это область науки, в которой существует наиболее глубокое взаимопроникновение физики, химии, биологии. В основе этого учения находятся химическая термодинамика и кинетика. Способность вещества подвергаться химическим превращениям определяется их реакционной способностью, т.е. природой реагирующих веществ – составом, строением, характером химической связи; энергетическими факторами, определяющими возможность протекания процесса и кинетическими факторами, определяющими скорость его протекания. Почти все химические процессы сопровождаются выделением или поглощением энергии, чаще всего в форме теплоты и работы. Теплота – количественная мера беспорядочного хаотичного движения частиц, образующих данную систему. Работа – количественная мера упорядоченного движения частиц в направленном силовом поле. Раздел химии, изучающей переходы энергии из одой формы в другую при химических реакциях и устанавливающая направление и пределы их самопроизвольного протекания при заданных условиях, называется химической термодинамикой. Объектом изучения химической термодинамики является химическая система. Система – это изучаемое тело или группа тел, которые взаимодействуют между собой и мысленно или реально отделены от окружающей среды границами, проводящими или не проводящими тепло. В зависимости от характера взаимодействия системы с окружающей средой различают открытые, закрытые и изолированные системы. Открытые системы могут обмениваться с окружающей средой энергией и веществом. Например, водный раствор хлорида натрия, находящийся в открытом сосуде. При испарении воды из раствора и при теплообмене будут меняться масса системы и ее температура, а, следовательно, и энергия. Закрытые системы не обмениваются с окружающей средой веществом. Например, раствор хлорида натрия в закрытом сосуде. Если раствор и окружающая среда имеют разную температуру, то будет происходить нагревание или охлаждение раствора, а, следовательно, будет меняться его энергия.
Изолированные системы не могут обмениваться со средой ни веществом, ни энергией. Изолированная система – это идеализация. В природе таких систем нет. Но, несмотря на невозможность практического воплощения, изолированные системы позволяют определять максимальные теоретические разности энергий между системой и ее окружением. Состояние системы определяется совокупностью свойств и характеризуется термодинамическими параметрами: температурой ( В термодинамики свойства системы рассматриваются в ее равновесных состояниях: начальных и конечных, вне зависимости от пути перехода системы из одного состояния в другое. Переход системы из одного состояния в другое при Важнейшими задачами химической термодинамики является выяснение возможности или невозможности самопроизвольного протекания процесса той или иной химической реакции при заданных условиях и в заданном направлении; установление значения термодинамических параметров, при которых достигается максимальный выход процесса; определение характеристик энергетического изменения, происходящего в системе. Находят это с помощью термодинамических функций ( Функция состояния
При этом
Приведенное уравнение представляет собой математическое выражение I закона термодинамики: если к системе подвести тепло, то подведенное тепло тратится на увеличение внутренней энергии системы и на совершение ей работы. В изохорно-изотермическом процессе вся теплота, подведенная к системе, тратится на изменение внутренней энергии:
В изобарно-изотермическом процессе единственным видом работы, совершаемой системой, является работа расширения:
где Тогда математическое выражение I закона термодинамики принимает вид: Обозначив Функция состояния системы Н – энтальпия – это общий запас энергии системы, т.е. это энергосодержание системы. Энтальпия системы больше внутренней энергии на величину работы. Для характеристики энергетических проявлений в ходе реакции введено понятие тепловой эффект. Тепловой эффект – это количество теплоты, которое выделяется или поглощается при необратимом протекании реакции, когда единственной работой будет работа расширения. При этом температуры исходных веществ и продуктов реакции должны быть одинаковыми. Тепловой эффект эндотермической реакции (протекает с поглощением тепла) будет положительным: Раздел химии, посвященный изучению тепловых эффектов химических реакций, называется термохимией. Всякая химическая реакция сопровождается изменениями запаса энергии реагирующих веществ. Чем больше энергии выделилось при образовании какого-либо химического соединения, тем это соединение устойчивее, и, наоборот, вещество, полученное в результате эндотермической реакции, неустойчивое. В химических уравнениях, в которых указана теплота реакции, называются термохимическими. Они составляются на основе законов сохранения массы и энергии. Для сравнения тепловых эффектов различных процессов стандартизуют условия их протекания. Стандартные условия - Т0= 298 К, р0 = 101,313 кПа, n – 1 моль чистого вещества, изменение энтальпии ( Из I закона термодинамики следуют количественные законы термохимии. Закон Лавуазье-Лапласа (1780 – 1784) – для каждого химического соединения теплота разложения равна теплоте его образования, но имеет противоположный знак.
Закон Г.И. Гесса (1840) – тепловой эффект химической реакции зависит от природы и физического состояния исходных веществ и конечных продуктов, но не зависит от характера и пути протекания реакции, т.е. от последовательности отдельных промежуточных стадий. Данный закон – теоретическая основа термохимии. Из него вытекает ряд следствий: - в термохимических расчетах теплота образования (энтальпия) простых веществ в стандартных условиях принимается равной нулю.
- количество энергии, которое выделяется или поглощается при образовании 1 моль сложного вещества из простых в стандартных условиях, называется стандартной энтальпией образования (
- количество энергии, которое выделяется или поглощается 1 моль органического вещества разлагающегося до углекислого газа и воды в стандартных условиях, называется стандартной энтальпией сгорания ( - тепловой эффект химической реакции равен разности между суммой теплот образования продуктов реакции и суммой теплот образования исходных веществ с учетом стехиометрических коэффициентов:
где Закон Гесса позволяет рассчитать тепловые эффекты различных реакций. Но знак и величина теплового эффекта не позволяет судить о способности процессов к самопроизвольному протеканию и не содержит информации о направлении и полноте протекания процессов. Самопроизвольные процессы (естественные или положительные) – протекают в системе без вмешательства со стороны внешней среды и сопровождаются уменьшением внутренней энергии системы и передачей энергии в окружающую среду в форме теплоты и работы. Эндотермические самопроизвольные процессы не противоречат этому определению, так как они могут протекать в неизолированной системе и производить работу за счет теплоты окружающей среды. Процессы, которые сами собой (без внешнего воздействия) совершаться не могут, называются несамопроизвольными, неестественными или отрицательными. Такие процессы осуществляются путем передачи системе энергии из внешней среды в форме теплоты или работы. Согласно II закону термодинамики самопроизвольные процессы идут в сторону уменьшения запаса внутренней энергии или энтальпии системы. Однако известны такие процессы, которые протекают самопроизвольно без изменения внутренней энергии системы. Движущей силой таких процессов является энтропия системы. Энтропия (связанная энергия) ( S) – это мера необратимости процесса, мера перехода энергии в такую форму, из которой она не может самостоятельно в другую энергию. Энтропия характеризует беспорядок в системе, чем выше беспорядок, тем выше энтропия. Она возрастает с увеличением движения частиц. В изолированных от внешней среды системах процессы протекают самопроизвольно в направлении увеличения энтропии (
Больцман вывел уравнение, согласно которому
Это соотношение показывает, что энтропию можно рассматривать как меру молекулярного беспорядка системы. Согласно II закону термодинамики для изотермического процесса изменение энтропии равно:
Энтропия простых веществ не равна нулю. В отличие от энтальпии, можно измерить абсолютное значение энтропии. «При абсолютном нуле энтропия идеального кристалла равна нулю» - этот постулат М. Планка (1911 г) называют III законом термодинамики. Изменение энтропии химического процесса определяется балансовым уравнением:
Любая система характеризуется порядком ( Таким образом, при самопроизвольном движении системы к устойчивому состоянию проявляются две тенденции: уменьшение энтальпии
Функция состояния Химические реакции протекают в открытом сосуде с изменением объема, поэтому возможность (самопроизвольность) и направление процесса характеризует функция
Самопроизвольному протеканию процесса отвечает уменьшение энергии Гиббса, Анализ величин
Таким образом, самопроизвольно протекают реакции, в которых изменение свободной энергии отрицательно. Реакции, в которых
Химические реакции, Химические реакции, протекающие самопроизвольно протекающие не самопроизвольно
экзотермические реакции, экзотермические реакции, сопровождающиеся сопровождающиеся возрастанием энтропии уменьшением энтропии
при любых температурах при высоких температурах эндотермические реакции сопровождающиеся возрастанием энтропии
при низких температурах
Рис. 3. Условия самопроизвольного протекания процесса.
3.2. Контрольные вопросы и задания 1. Что называется системой? Какими параметрами характеризуется система? 2. Охарактеризуйте внутреннюю энергию системы, понятие об изохорных и изобарных процессах. 3. Что называется энтальпией? 4. Охарактеризуйте энтальпию образования соединений, стандартные энтальпии сгорания и образования веществ. 5. Закон Гесса и его следствия, его применение в термохимических расчетах. 6. Определение теплот (энтальпий) нейтрализации, растворения, гидратации. 7. Энтропия. Уравнение Больцмана. Как изменяется энтропия с изменением температуры? 8. Энергия Гиббса. Критерии самопроизвольного протекания процесса. 9. Пользуясь справочными данными приложения 3, вычислите изменение стандартной энтальпии реакции ( 10. Пользуясь справочными данными приложения 3, вычислите изменение стандартной энтропии реакции ( 11. Вычислить
Примеры решения задач Пример 1. Реакция горения этилового спирта выражается термохимическим уравнением С2Н5ОН(Ж) + 3О2(Г) = 2СО2(Г) + 3Н2О(Ж). Вычислите тепловой эффект реакции, если известно, что молярная теплота парообразования С2Н5ОН(Ж) равна +42,36 кДж, а теплоты образования С2Н5ОН(Г) = -235,31 кДж, СО2(Г) = -393,51 кДж, Н2О(Ж) = -285,84 кДж. Решение. Для определения ΔΗ реакции необходимо знать теплоту образования С2Н5ОН(Ж). Последнюю находим из данных: С2Н5ОН(Ж) = С2Н5ОН(Г); ΔΗ = +42,36 кДж +42,36 = -235,31 – ΔΗ(С2Н5ОН(Ж)) ΔΗ(С2Н5ОН(Ж)) = -235,31-42,36 = -277,67 кДж Вычисляем ΔΗ реакции, применяя следствия из закона Гесса: ΔΗХ.Р. = 2(-393,51) + 3(-285,84) + 277,67 = -1366,87 кДж. Тепловой эффект реакции 1366,87 кДж. Пример 2. Рассчитать ΔΗХР восстановления оксида железа (III) различными восстановителями при стандартных условиях: а) Fe2O3(К) + 3H2(Г) = 2Fe(К) + 3H2O(Г) б) Fe2O3(К) + 3СО(Г) = 2Fe(К) + 3СО2(Г) В каком случае на этот процесс потребуется больше затратить энергии? Решение. Для расчета ΔΗХР воспользуемся формулой следствия из закона Гесса и стандартными энтальпиями образования каждого вещества [Приложение 3]: а) ΔΗХР = 2ΔΗ(Fe) + 3ΔΗ(H2O) – (ΔΗ(Fe2O3) + 3ΔΗ(H2)) = 2(0) + 3(-241,8) – ((-822,2) + 3(0)) = -725,4 + 822,2 = 96,8 кДж. б) ΔΗХР = 2ΔΗ(Fe) + 3ΔΗ(СO2) – (ΔΗ(Fe2O3) + 3ΔΗ(СО)) = 2(0) + 3(-393,5) – ((-822,2) + 3(-110,5)) = -1180,5 + 822,2 + 331,5 = -26,5 кДж. Согласно расчетам, процесс а) – восстановление оксида железа (III) водородом, требует больше затрат энергии, чем процесс б). В процессе б) реакция даже носит экзотермический характер (выделяется энергия в виде тепла). Пример 3. Водяной газ представляет собой смесь равных объемов водорода и оксида углерода (II). Найдите количество теплоты, выделяющейся при сжигании 112 л водяного газа, (н.у.). Решение. Составим термохимическое уравнение процесса: Н2(Г) + СО(Г) + О2(Г) = Н2О(Г) + СО2(Г) ΔΗХР = - Q. Рассчитаем ΔΗХР, когда сгорает 2 моля водяного газа (1 моль Н2 и й моль СО), т.е. 22,4 л/моль · 2 моль = 44,8 л. Расчет ведем по формуле следствия закона Гесса и стандартными энтальпиями образования каждого вещества [Доп. 3]: ΔΗХР = ΔΗ(Н2О) + ΔΗ(СО2) – (ΔΗ(Н2) + ΔΗ(СО) + ΔΗ(О2)) = -241,8 – 393,5 – (0 – 110,5 + 0) = - 635,3 + 110,5 = - 524,8 кДж Составляем пропорцию: Сгорает 44,8 л водяного газа – выделяется 524,8 кДж тепла 112 л - Х кДж Х = 112 · 524,8 / 44,8 = 1312 кДж При сжигании 112 л водяного газа выделяется 1312 кДж тепла. Пример 4. Дайте термодинамическую характеристику процесса Ga + HCl) ↔ GaCl3(т) + Н2(г) по плану: 1. Запишите стехиометрическое уравнение. 2. Выпишите термодинамические функции участвующих веществ. 3. Рассчитайте изменение стандартной энтальпии химической реакции и постройте энтальпийную диаграмму. 4. Определите, является реакция экзо- или эндотермической; увеличивается или уменьшается температура в системе в результате протекания данной реакции. 5. Рассчитайте изменение стандартной энтропии реакции, объясните изменение энтропии в ходе реакции. 6. Рассчитайте стандартное изменение энергии Гиббса по балансовому уравнению и уравнению Гиббса. Дайте анализ полученным данным. 7. Сопоставьте знаки величин 8. Для обратимой реакции рассчитайте равновесную температуру согласно уравнению Гиббса допуская, что предельно допустимой температурой является 3000 К. Сделайте вывод: Тр – реализуема или не реализуема. 9. Рассчитайте величину 10. Сделайте вывод о самопроизвольности протекания химической реакции. Определите условия, при которых реакция возможна Решение. 1 Записываем стехиометрическое уравнение.
2. Выписываем стандартные термодинамические функции образования компонентов реакции (табл. 21) (термодинамические параметры веществ из [Приложение 3]). Таблица 21
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.132.253 (0.015 с.) |

 ), давлением (
), давлением (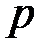 ), объемом (
), объемом ( ), плотностью (
), плотностью ( ), количеством вещества (
), количеством вещества ( ), совершаемой работой (
), совершаемой работой ( ), теплотой (
), теплотой ( ). Изменение хотя бы одного термодинамического параметра приводит к изменению состояния системы в целом. Если все параметры постоянны во времени и пространстве, то такое состояние системы называется равновесным.
). Изменение хотя бы одного термодинамического параметра приводит к изменению состояния системы в целом. Если все параметры постоянны во времени и пространстве, то такое состояние системы называется равновесным. ).
). характеризует внутреннюю энергию системы – сумму потенциальной энергии взаимодействия всех частиц тела между собой и кинетической энергии их движения. Она зависит от состояния вещества – вида, массы, агрегатного состояния. Абсолютную величину внутренней энергии измерить невозможно. Для изучения химических процессов важно знать только изменение внутренней энергии при переходе системы из одного состояния в другое.
характеризует внутреннюю энергию системы – сумму потенциальной энергии взаимодействия всех частиц тела между собой и кинетической энергии их движения. Она зависит от состояния вещества – вида, массы, агрегатного состояния. Абсолютную величину внутренней энергии измерить невозможно. Для изучения химических процессов важно знать только изменение внутренней энергии при переходе системы из одного состояния в другое. (27)
(27)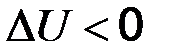 внутренняя энергия системы убывает, при
внутренняя энергия системы убывает, при  - возрастает. Все изменения внутренней энергии происходят за счет хаотического столкновения молекул (мерой передаваемой таким способом энергии является теплота) и перемещения масс, состоящих из большого числа частиц, под действием каких-либо сил (мерой передаваемой таким способом энергии является работа). Таким образом передача внутренней энергии может осуществляться частично в виде теплоты и частично в виде работы:
- возрастает. Все изменения внутренней энергии происходят за счет хаотического столкновения молекул (мерой передаваемой таким способом энергии является теплота) и перемещения масс, состоящих из большого числа частиц, под действием каких-либо сил (мерой передаваемой таким способом энергии является работа). Таким образом передача внутренней энергии может осуществляться частично в виде теплоты и частично в виде работы: (28)
(28) (29)
(29) (30)
(30) - давление в системе,
- давление в системе, 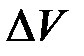 - изменение объема
- изменение объема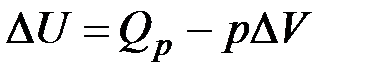 (31)
(31)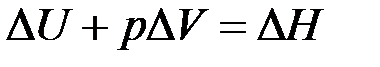 , получаем
, получаем 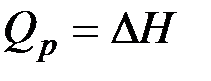
 ,
, 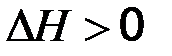 . Тепловой эффект экзотермической реакции (протекает с выделением тепла) будет отрицательным:
. Тепловой эффект экзотермической реакции (протекает с выделением тепла) будет отрицательным:  ,
, 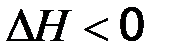 .
. ) относят к единице количества вещества, кДж/моль. Все стандартные термодинамические функции – это табличные величины, которые зависят от агрегатного состояния вещества.
) относят к единице количества вещества, кДж/моль. Все стандартные термодинамические функции – это табличные величины, которые зависят от агрегатного состояния вещества. (32)
(32) (простого вещества) = 0
(простого вещества) = 0 , кДж/моль).
, кДж/моль). , кДж/моль).
, кДж/моль). (33)
(33)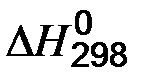 - тепловой эффект химической реакции в стандартных условиях;
- тепловой эффект химической реакции в стандартных условиях;  - сумма стандартных теплот образования продуктов реакции;
- сумма стандартных теплот образования продуктов реакции; 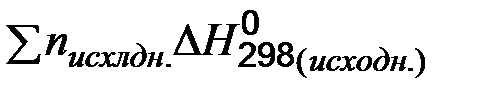 - сумма стандартных теплот образования исходных веществ;
- сумма стандартных теплот образования исходных веществ;  ,
,  - стехиометрические коэффициенты соответственно продуктов реакции и исходных веществ.
- стехиометрические коэффициенты соответственно продуктов реакции и исходных веществ. ). Процессы, для которых энтропия уменьшается (
). Процессы, для которых энтропия уменьшается ( ) неосуществимы в изолированных системах. Если процесс возможен в прямом и обратном направлениях, то в изолированной системе он будет протекать в направлении возрастания энтропии. Протекание самопроизвольного процесса в изолированной системе завершается состоянием равновесия. Следовательно, в состоянии равновесия энтропия системы максимальна.
) неосуществимы в изолированных системах. Если процесс возможен в прямом и обратном направлениях, то в изолированной системе он будет протекать в направлении возрастания энтропии. Протекание самопроизвольного процесса в изолированной системе завершается состоянием равновесия. Следовательно, в состоянии равновесия энтропия системы максимальна.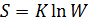 (34) где
(34) где  - постоянная Больцмана, W – вероятность состояния, определяет число микросостояний, соответствующих данному микросостоянию.
- постоянная Больцмана, W – вероятность состояния, определяет число микросостояний, соответствующих данному микросостоянию. ; [Дж/(моль·К] (35)
; [Дж/(моль·К] (35) (36)
(36) ) и беспорядком (
) и беспорядком ( ). Их соотношение определяет направление протекания реакции.
). Их соотношение определяет направление протекания реакции. и возрастание энтропии
и возрастание энтропии  ).
).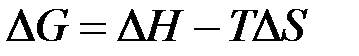 (37)
(37) - часть энергии, которая не может быть превращена в полезную работу («связанная энергия»).
- часть энергии, которая не может быть превращена в полезную работу («связанная энергия»). ;
;  (38)
(38) . Чем больше уменьшается
. Чем больше уменьшается  является признаком неосуществимости процесса в данных условиях. Значение
является признаком неосуществимости процесса в данных условиях. Значение  характеризует состояние равновесия, т.е. состояние, в котором система не производит полезной работы.
характеризует состояние равновесия, т.е. состояние, в котором система не производит полезной работы. в уравнении Гиббса показал, что возможность обратимого протекания процесса обусловлена одинаковыми знаками
в уравнении Гиббса показал, что возможность обратимого протекания процесса обусловлена одинаковыми знаками  ):
):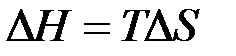 ;
; 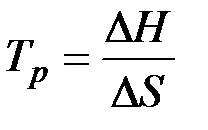 (39)
(39)

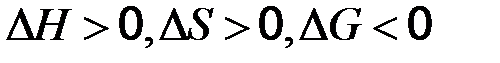
 ):
): 
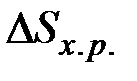 ):
): 
 реакции при 8460 С, если
реакции при 8460 С, если 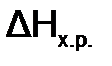 . и
. и  Сделайте вывод об обратимости реакции.
Сделайте вывод об обратимости реакции. при трех значениях температур (500, 1000 и 1500 К). Постройте графическую зависимость
при трех значениях температур (500, 1000 и 1500 К). Постройте графическую зависимость  ..
..



