
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корпускулярно-волновые свойства частицСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Характеристика состояния электронов в атоме основана на положении квантовой механики о двойственной природе электрона, обладающего одновременно свойствами частицы и волны. Впервые двойственная корпускулярно-волновая природа была установлена для света. Исследования ряда явлений (излучение раскаленных тел, фотоэффект, атомные спектры) привели к выводу, что энергия испускается и поглощается не непрерывно, а дискретно, отдельными порциями (квантами). Предположение о квантовании энергии впервые было высказано Максом Планком (1900 г.) и обосновано Альбертом Эйнштейном (1905 г.): энергия кванта (∆Е) зависит от частоты излучения (ν): ∆Е = hν, где h = 6,63·10-34 Дж·с – постоянная Планка. Приравнивая энергию фотона hν к полному запасу его энергии mс2 и, учитывая, что ν=с/λ, получаем соотношение выражающее взаимосвязь волновых и корпускулярных свойств фотона:
В 1924 году Луи де Бройль предположил, что двойственная корпускулярно-волновая природа присуща не только излучению, но и любой материальной частице: каждой частице, имеющей массу(m) и движущейся со скоростью (υ) соответствует волновой процесс с длиной волны λ: λ = h / m υ (55) Чем меньше масса частицы, тем больше длина волны. Поэтому обнаружить волновые свойства у макрочастиц трудно. В 1927 г. Американские ученые Девиссон и Джермер, англичанин Томсон и советский ученый Тартаковский независимо друг от друга обнаружили дифракцию электронов, что явилось экспериментальным подтверждением волновых свойств электронов. Позднее была открыта дифракция (интерференция) α-частиц, нейтронов, протонов, атомов и даже молекул. В настоящее время дифракция электронов используется для исследования строения вещества. В волновых свойствах элементарных частиц заложен один из принципов волновой механики: принцип неопределенности (В. Гейзенберг 1925 г.): для малых тел атомного масштаба невозможно одновременно точно определить положение частицы в пространстве и ее скорость (импульс). Сем точнее определены координаты частицы, тем менее определенной становится ее скорость, и наоборот. Соотношение неопределенностей имеет вид:
где ∆х – неопределенность положения частицы, ∆Рх – неопределенность величины импульса или скорости в направлении х. Аналогичные соотношения записываются и для координат y и z. Величина ℏ, входящая в соотношение неопределенности, очень мала, поэтому для макрочастиц неопределенности в значениях координат и импульсов ничтожны.
Следовательно, нельзя рассчитать траекторию движения электрона в поле ядра, можно лишь оценить вероятность его нахождения в атоме с помощью волновой функции ψ, которая заменяет классическое понятие траектории. Волновая функция ψ характеризует амплитуду волны в зависимости от координат электрона, а ее квадрат ψ2 определяет пространственное распределение электрона в атоме. В наиболее простом варианте волновая функция зависит от трех пространственных координат и дает возможность определить вероятность нахождения электрона в атомном пространстве или его орбиталь. Таким образом, атомная орбиталь (АО) – область атомного пространства, в котором вероятность нахождения электрона наибольшая. Волновые функции получаются при решении основополагающего соотношения волновой механики – уравнения Шредингера (1926 г):
где h- постоянная Планка, Таким образом, квантование энергии микросистемы вытекает непосредственно из решения волнового уравнения. Волновая функция полностью характеризует состояние электрона. Волновая функция системы – это функция состояния системы, квадрат которой равен плотности вероятности нахождения электронов в каждой точке пространства. Она должна удовлетворять стандартным условиям: быть непрерывной, конечной, однозначной, обращаться в нуль там, где электрон отсутствует. Точное решение получается для атома водорода или водородоподобных ионов, для многоэлектронных систем используются различные приближения. Поверхность, ограничивающая 90–95 % вероятности нахождения электрона или электронной плотности, называют граничной. Атомная орбиталь и плотность электронного облака имеют одинаковую граничную поверхность (форму) и одинаковую пространственную ориентацию. Атомные орбитали электрона, их энергия и направление в пространстве зависят от четырех параметров – квантовых чисел: главного, орбитального, магнитного и спинового. Первые три характеризуют движение электрона в пространстве, а четвертое – вокруг собственной оси.
Квантовое число n – главное. Оно определяет энергетический уровень электрона в атоме, удаленность уровня от ядра и размер электронного облака. Принимает целые значения от 1 до ∞ и соответствует номеру периода. Из периодической системы для любого элемента по номеру периода можно определить число энергетических уровней атома, и какой энергетический уровень является внешним. Чем больше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном. Если n ∞, то электрон покинул атомный объем. Произошла ионизация атома.
Например, элемент кадмий Cd расположен в пятом периоде, значит n=5. В его атоме электроны распределены по пяти энергетическим уровням (n = 1, n = 2, n = 3, n = 4, n = 5); внешним будет пятый уровень (n = 5). Так как электрон обладает наряду со свойствами волны и свойствами материальной частицы, то он, обладая массой m, скоростью движения V, и находясь на расстоянии от ядра r, обладает моментом количества движения: μ=mVr. Момент количества движения – это вторая (после энергии) характеристика электрона и выражается через побочное (азимутальное, орбитальное) квантовое число. Орбитальное квантовое число l - определяет форму электронного облака (рис. 7), энергию электрона на подуровне, количество энергетических подуровней. Принимает значения от 0 до n – 1. Кроме числовых значений l имеет буквенные обозначения. Электроны с одинаковым значением l образуют подуровень.
В каждом квантовом уровне число подуровней строго ограничено и равно номеру слоя. Подуровни, как и энергетические уровни, нумеруются в порядке их удаления от ядра (табл. 26). Таблица 26
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.88.132 (0.011 с.) |

 (54)
(54) (
( )
) 
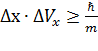 (56)
(56) (57)
(57) - переменная величина, U – потенциальная энергия частицы, Е – полная энергия частицы, x, y,z, - координаты.
- переменная величина, U – потенциальная энергия частицы, Е – полная энергия частицы, x, y,z, - координаты.


