
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематические характеристики частицыСодержание книги
Поиск на нашем сайте
Динамические характеристики частицы. Законы Ньютона Основные принципы классической механики были сформулированы в 1687 г. И. Ньютоном в книге «Математические начала натуральной философии». Законы Ньютона в авторской формулировке (перевод А.Н. Крылова): I закон: Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. II закон: Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. III закон: Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны. Дадим законам Ньютона современную трактовку. I закон постулирует существование инерциальной системы отсчета (ИСО), т. е. такой системы отсчета, в которой все изолированные (свободные, не подверженные внешним воздействиям) материальные точки движутся равномерно и прямолинейно (или покоятся). Понятие ИСО – идеализация. В ИСО имеет место явление инерции – равномерное и прямолинейное движение свободного тела (частицы). II закон описывает движение материальной точки относительно ИСО, в том числе и несвободной (подверженной воздействию). Любое физическое тело обладает инертностью – свойством препятствовать изменению его скорости относительно ИСО. Мера инертности – масса. В классической механике масса – аддитивная величина (масса тела равна сумме масс его частей). Величина, определяемая произведением массы тела на его скорость – импульс (количество движения):
Импульс свободной частицы в ИСО не изменяется с течением времени (сохраняется), т. к. свободная частица движется по инерции, а масса частицы в классической механике неизменна. Для изменения импульса частицы в ИСО необходимо воздействие на нее других материальных объектов. Такое воздействие характеризуется векторной физической величиной – силой. Чем больше сила, тем быстрее изменяется импульс частицы в ИСО. Современная формулировка II закона: производная импульса материальной точки по времени равна силе, действующей на материальную точку в ИСО:
При
Тогда II закон Ньютона можно переформулировать: ускорение материальной точки относительно ИСО прямо пропорционально действующей силе и обратно пропорционально массе. В соответствующей системе единиц
Заметим, что с помощью (1.5.4) можно определить силу и массу независимо друг от друга, задавая эталоны этих величин и измеряя ускорения кинематически. В I и II законах говорится об одном отдельно взятом теле (частице); воздействие на него других тел рассматривается без анализа последствий этого воздействия для последних. В III законе рассматривается система из двух тел: силы, с которыми две материальные точки действуют друг на друга, равны по модулю и направлены в противоположные стороны по прямой, проходящей через эти точки:
Дополнением к законам Ньютона служит принцип суперпозиции сил: ускорение, получаемое частицей при одновременном действии на нее нескольких сил, определяется геометрической суммой ускорений, получаемых частицей при действии каждой из этих сил в отдельности:
Если речь идет об одной частице, подверженной действию нескольких сил, то величина
называется равнодействующей силой. В этом случае под «силой» в форму-лировке II закона Ньютона следует понимать именно равнодействующую силу. Заметим, что при
Принцип относительности Галилея. Механическая концепция Взаимодействия Обратимся к преобразованиям Галилея для координат и скоростей. Легко видеть, что частица, движущаяся в СК 01 XYZ с постоянной скоростью
Оказывается, что все ИСО эквивалентны и физически. В классической механике постулируется, что все ИСО эквивалентны для механических взаимодействий. Это утверждает принцип относительности Галилея, суть которого в том, что любой механический процесс происходит во всех ИСО по одним и тем же законам, имеющим инвариантную форму. Имеются также неизменные величины – инварианты преобразований Галилея (ускорение, масса, сила). Они особенно существенны при изучении движения, т. к. выражают одинаковые во всех ИСО свойства тел и движений. II закон Ньютона не только сохраняет свою форму во всех ИСО, но и связывает инвариантные величины. III закон Ньютона и принцип независимого действия сил также справедливы во всех ИСО. В классической механике все ИСО равноправны, привилегированной или абсолютно неподвижной системы отсчета нет. Остановимся подробнее на концепциях взаимодействия в механике. Заметим, что изучение природы сил не входит в задачи механики и выполняется в других разделах физики. По данному вопросу можно высказать лишь самые общие соображения, вытекающие из моделей материальных объектов и взаимодействий между ними, принятых в механике. Исходной для механики является система материальных точек в пустоте, связанных мгновенно передающимся взаимодействием. Силы взаимодействия между любыми двумя частицами центральные и подчиняются III закону Ньютона. Силы, действующие на частицу со стороны других частиц, могут зависеть от относительных расстояний, а эти расстояния – от положения рассматриваемой частицы в пространстве. Поэтому равнодействующая сила – функция координат частицы, а также времени, поскольку частицы могут двигаться:
К механическим силам относят также контактные силы (упругости и трения), возникающие при соприкосновении макроскопических тел. Задача о подробном рассмотрении взаимодействия на уровне микрочастиц в механике не ставится, а рассматривается и эмпирически определяется суммарный макроскопический эффект. Для двух тел, взаимодействующих посредством контактных сил, справедлив III закон Ньютона. В рамки механической концепции укладываются основные известные проявления гравитационного взаимодействия и частично электромагнитного. Сильное и слабое взаимодействия не соответствуют механической концепции в главном: для них исключено применение модели дальнодействия. Однако, математическая концепция, несмотря на привлекательную математическую простоту, не может быть положена в основу физической картины всего материального мира. Главный ее недостаток – отсутствие в системе материальных тел материальных полей, взаимодействующих с телами. Поля передают взаимодействие между телами с большой, но не бесконечной скоростью, действуя на частицу там, где она находится в поле (близкодействие).
Рассмотрим последствия включения поля в механическую систему. Поле непрерывно заполняет пространство. Основное его механическое действие силовое: частицы в поле приобретают ускорения. Для сил, действующих в физических полях на частицы, справедлив II закон Ньютона, если движение частицы не изменяет существенно параметры поля и частицей (материальной точкой) моделируется физическое макроскопическое тело. Взаимодействие от частицы к частице передается с конечной скоростью с за время Движение макроскопических тел с нерелятивистскими скоростями происходит в сравнительно слабых и медленно изменяющихся полях (гравитационном и электромагнитном), поэтому данное движение можно изучать в механике без применения понятия материального поля. В физике же микромира механическая концепция взаимодействия не применима из-за возможности существования нецентральных сил взаимодействия между частицами, из-за релятивистских скоростей, из-за взаимопревращений частиц и т. д. Механической причинности Дифференциальное уравнение движения частицы массой m в силовом поле в векторной форме записи имеет вид:
Это основное уравнение нерелятивистской динамики частицы. Оно может рассматриваться как исходное положение (постулат), из которого путем математических преобразований получают как общие следствия и выводы классической механики, так и решения ее конкретных задач. Все механические движения подчиняются этому уравнению, в котором m – скалярный параметр, характеризующий свойства частицы,
С помощью данного уравнения ставятся и решаются две важнейшие задачи динамики частицы. Первая задача (или прямая задача): дан закон движения Задача решается двойным дифференцированием по времени кинематического уравнения движения Вторая (обратная) задача: известно силовое поле, в котором движется частица массой m; требуется найти закон движения частиц. Приведем алгоритм решения обратной задачи динамики частицы в декартовых координатах. Известно
Общее решение этой системы уравнений имеет вид:
где Наличие произвольных постоянных в общем интеграле показывает, что он представляет не конкретное движение, а дает кинематические уравнения непрерывного семейства движений с одинаковыми ускорениями. Например, кинематические уравнения и траектории движения частицы под действием силы тяжести зависят от начальных условий (тела, брошенные вертикально вверх, горизонтально, под углом к горизонту движутся по-разному), хотя динамическое уравнение движения
а также
(1.7.4) и (1.7.5) образуют систему из шести независимых уравнений, из которых можно выразить постоянные
Таким образом, обратная задача динамики частицы решена. Заметим, что зачастую дифференциальные уравнения движения можно решить лишь с использованием численных методов. Полное решение второй задачи динамики не требуется, если известны первые интегралы движения. Рассмотрим смысл первых интегралов. Добавляя к (1.7.3) уравнения
получим систему уравнений относительно неизвестных
Выражая из последнего уравнения время t и подставляя его значение в остальные уравнения, получим:
Поскольку Знание некоторых интегралов движения сразу дает ответы на частные вопросы. Поэтому установление признаков существования интегралов дви-жения и их нахождение – важная задача динамики частицы. Основное уравнение динамики и общий анализ его решения позволяют установить причинно-следственные связи при механическом движении. Состояние механической системы считается в данный момент заданным, если известны массы каждой частицы, координаты и скорости. Можно утверждать, что состояние в данный момент времени предопределяет (причем однозначно) состояние данной системы в любой другой момент времени. Такая однозначная связь причины и следствия носит название динамической закономерности. Классическая механика относится к теориям с динамической закономерной связью между причинами и следствиями. Принцип механической причинности в классической механике: состояние системы материальных точек однозначно определяется их взаимодействием и начальными условиями.
Вариационной концепции Уравнения Лагранжа были получены из уравнений Ньютона для системы частиц с помощью принципа виртуальных перемещений и принципа д¢Аламбера-Лагранжа. Однако уравнения Лагранжа можно получить из общего теоретического принципа экстремального действия, установленного Гамильтоном и обобщенного Остроградским. Этот принцип распространяется не только на механические, но и на квантово-механические системы, а также на поля как системы с бесконечно большим числом степеней свободы. Принцип экстремального действия позволяет получать фундаментальные уравнения физики в различных ее разделах и поэтому имеет важнейшее теоретическое значение. Согласно этому принципу каждая механическая система характеризуется определенной функцией
При этом функция Специальными методами аналитической механики доказывается, что для малых интервалов времени В математике интеграл вида (2.5.1) принадлежит к так называемым функционалам, если рассматривать зависимость его величины от вида подынтегральной функции. Задача об экстремуме функционала (отыскание функции, при которой имеет место экстремум) решается методами вариационного исчисления. В результате находятся дифференциальные уравнения, выполняющиеся для подынтегральной функции. В нашем случае Рассмотрим сначала одномерную задачу:
Изменяя последовательность дифференцирования и варьирования (время не варьируется), получаем
Второй интеграл берется по частям:
Первое слагаемое (2.5.6) обращается в нуль, т. к. по определению ищется функция
причем это должно выполняться при любых
а это и есть уравнение Лагранжа для обобщенно-потенциальных сил. Обобщить (2.5.8) на систему
Особенность принципа экстремального действия – простая его связь с преобразованиями от одной системы отсчета к другой. Если действие является инвариантом некоторых преобразований, то получаемые из соответствующей функции Пусть механическая система состоит из двух частей Это свойство аддитивности функции Лагранжа говорит о том, что уравнения движения каждой из невзаимодействующих частей не могут содержать величины, относящиеся к другим частям системы. Очевидно, умножение функции Лагранжа на произвольную постоянную не отражается на уравнениях движения описываемой ею системы частиц. Свойство аддитивности допускает лишь одновременное умножение лагранжевых функций всех рассматриваемых систем на одинаковую постоянную, что сводится к естественному произволу в выборе единиц измерения для Функция Лагранжа определяется с точностью до прибавления к ней полной производной от любой функции координат и времени. В самом деле, если
Тогда Построение классической механики как физической теории возможно на различных исходных положениях и принципах. Такие принципы могут различаться по своей общности и математической форме, хотя и связаны между собой. Каждая из схем построения механики содержит некоторую новую точку зрения на описание механического движения. Это имеет большую эвристическую ценность: особенности механического движения, остающиеся скрытыми при одних исходных принципах, выступают явно при использовании других. По математической форме принципы выражаются дифференциальными или интегральными соотношениями. Дифференциальными называют такие законы, формулы которых связывают значения величин, относящиеся к одному и тому же моменту времени или к одной и той же точке пространства. Формулы интегральных законов устанавливают связь между величинами, относящимися к конечному промежутку времени или к конечной области пространства. Принципы механики подразделяются ещё на вариационные и невариационные. Невариационные законы устанавливают соотношения между величинами, имеющими место для действительного движения. Вариационные устанавливают признаки, отличающие действительное движение от всех других кинематически возможных движений. Примеры вариационных дифференциальных принципов: принцип виртуальных перемещений, принцип д¢Аламбера-Лагранжа (общее уравнение механики). Известны интегральные вариационные принципы, обладающие той или иной степенью общности (наиболее общий – принцип Гамильтона-Остроградского). Схема построения классической механики, основанная на законах Ньютона, из которых следует все содержание положений и выводов механики, имеет отличительную черту: подход к силе как к причине изменения механического состояния (такой подход в известной мере нагляден). Другая схема имеет в своей основе интегральный вариационный принцип Гамильтона-Остроградского. В физическом плане она более формальна, но зато и более общая, т. к. распространяется за пределы классической механики. Исходные понятия здесь – лагранжиан и действие; они весьма абстрактны. Принцип экстремального действия находит применение в различных разделах теоретической физики, что связано с методом обобщенных координат, благодаря которому уравнения Лагранжа не ограничены евклидовым пространством. Переход к бесконечномерному пространству конфигураций позволяет применять принцип экстремального действия к системам с бесконечно большим числом степеней свободы – физическим полям. Подчеркнем, что в первой схеме построения механики должны быть заданы силы, во второй – функция Лагранжа (или, как будет показано ниже, функция Гамильтона). Конкретные формулы как для сил, так и для указанных функций, в механике не выводятся, а задаются.
Сохранения При движении механической системы Рассмотрим механическую систему, в которой действуют обобщенно-потенциальные силы, т. е. силы, удовлетворяющие условию
где
Умножив каждое из уравнений (3.1.2) на соответствующую обобщенную скорость и просуммировав результаты, после преобразований (см. подробнее в [4, с. 193–194]) получим:
Функция
называется обобщенной энергией системы (функцией Гамильтона или гамильтонианом). Итак, (3.1.3) можно переписать в виде:
Это еще одна форма записи уравнений Лагранжа. Отсюда следует закон сохранения обобщенной энергии: если функция Лагранжа явно от времени не зависит, то обобщенная энергия системы сохраняется во времени:
В частности, для консервативных сил можно показать (см. [4, с. 194]), что обобщенная энергия равна полной механической энергии системы, которая сохраняется, т. е. закон сохранения механической энергии – частный случай закона сохранения обобщенной энергии. Величину называют обобщенным импульсом, соответствующим обобщенной координате
Лагранжиан может быть независимым от некоторых обобщенных координат, которые в этом случае называют циклическими. С каждой такой координатой связан первый интеграл движения. Закон сохранения обобщенного импульса: если обобщенная координата циклическая, то соответствующий ей обобщенный импульс сохраняется:
В частном случае консервативных сил при Заметим, что для системы, свободной от связей, в качестве обобщенных координат можно выбрать декартовы координаты частиц системы. В этом случае обобщенные скорости – производные этих координат по времени. Но при обобщенно-потенциальных силах обобщенные импульсы отличаются от обычных импульсов вида
Задача Кеплера Частный случай задачи о движении частицы в центральном поле – задача о движении в поле притяжения кулоновского типа (например, задача о движении в поле тяготения). В этом случае Известно, что в рассматриваемом случае
Тогда функцию Лагранжа т. е. рассматривается движение частицы с обобщенной координатой
Заметим, что (4.3.3) можно получить и непосредственным дифференцированием механической энергии Тогда из (4.3.3) находим:
где
Это формула Бине – дифференциальной уравнение траектории при заданной силе. Если
знак
Постоянная Учитывая, что
где
В частности, для поля тяготения
где Для описания движения двух тел с массами Это неоднородное дифференциальное уравнение второго порядка, общее решение которого
где В полярных координатах уравнение конического сечения
где
Вид траектории определяют константы | |||||||
|
| Поделиться: |

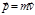 . (1.5.1)
. (1.5.1)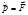 . (1.5.2)
. (1.5.2)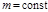 из (1.5.2) имеем:
из (1.5.2) имеем: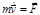 или
или 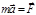 .(1.5.3)
.(1.5.3)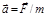 . (1.5.4)
. (1.5.4)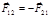 . (1.5.5)
. (1.5.5)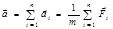 . (1.5.6)
. (1.5.6)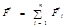 (1.5.7)
(1.5.7)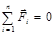 ускорение тела
ускорение тела  , т. е. в ИСО тело ведет себя как свободное, хотя таковым не является. Поэтому недопустимо трактовать I закон Ньютона как следствие II закона: I закон постулирует существование ИСО, а II закон определяет характер движения тела в ИСО.
, т. е. в ИСО тело ведет себя как свободное, хотя таковым не является. Поэтому недопустимо трактовать I закон Ньютона как следствие II закона: I закон постулирует существование ИСО, а II закон определяет характер движения тела в ИСО. , в СК 0 xyz также движется с постоянной скоростью
, в СК 0 xyz также движется с постоянной скоростью  , хотя и иной по величине. Следовательно, если одна из систем отсчета инерциальная, то и любая другая, движущаяся относительно нее равномерно, прямолинейно и поступательно, также инерциальная. Свойства симметрии пространства и времени, постулированные для одной из ИСО справедливы для пространства и времени в любой другой ИСО, в силу линейности преобразований Галилея. Все ИСО геометрически эквивалентны.
, хотя и иной по величине. Следовательно, если одна из систем отсчета инерциальная, то и любая другая, движущаяся относительно нее равномерно, прямолинейно и поступательно, также инерциальная. Свойства симметрии пространства и времени, постулированные для одной из ИСО справедливы для пространства и времени в любой другой ИСО, в силу линейности преобразований Галилея. Все ИСО геометрически эквивалентны. . Таким образом, мы приходим к понятию силового поля – области пространства, в каждой точке которого на частицу действует сила, зависящая от координат и времени. Такое понятие силового поля полностью согласуется с механической моделью материальных объектов и концепцией взаимодействия. Но такое поле не материальный объект, входящий в механическую систему, а просто удобное вспомогательное математическое понятие, позволяющее вместо подробного рассмотрения всех попарных взаимодействий использовать выражение вида
. Таким образом, мы приходим к понятию силового поля – области пространства, в каждой точке которого на частицу действует сила, зависящая от координат и времени. Такое понятие силового поля полностью согласуется с механической моделью материальных объектов и концепцией взаимодействия. Но такое поле не материальный объект, входящий в механическую систему, а просто удобное вспомогательное математическое понятие, позволяющее вместо подробного рассмотрения всех попарных взаимодействий использовать выражение вида  . В рамках рассматриваемой механической концепции равнодействующая сила может быть также функцией скорости данной частицы, поэтому в общем случае
. В рамках рассматриваемой механической концепции равнодействующая сила может быть также функцией скорости данной частицы, поэтому в общем случае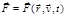 . (1.6.1)
. (1.6.1)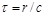 (время запаздывания), что нарушает равенство действия и противодействия – III закон Ньютона не выполняется. В чистом виде основная механическая модель (система частиц и дальнодействие) может применяться, если материальное поле можно заменить силовым, а последнее правомерно, если временем запаздывания можно пренебречь (т. е. при скорости частицы
(время запаздывания), что нарушает равенство действия и противодействия – III закон Ньютона не выполняется. В чистом виде основная механическая модель (система частиц и дальнодействие) может применяться, если материальное поле можно заменить силовым, а последнее правомерно, если временем запаздывания можно пренебречь (т. е. при скорости частицы 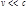 ). Кроме того, поле должно изменяться сравнительно медленно, чтобы во время запаздывания его можно было бы считать стационарным.
). Кроме того, поле должно изменяться сравнительно медленно, чтобы во время запаздывания его можно было бы считать стационарным.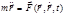 . (1.7.1)
. (1.7.1)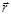 – радиус-вектор,
– радиус-вектор, 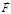 – некоторая однозначная, конечная и непрерывная функция координат, скорости и времени, которая может быть определена независимо. Постулируется именно этот общий вид уравнения (то, что его правую часть называют силой, ничего от объективности закона движения не отнимает).
– некоторая однозначная, конечная и непрерывная функция координат, скорости и времени, которая может быть определена независимо. Постулируется именно этот общий вид уравнения (то, что его правую часть называют силой, ничего от объективности закона движения не отнимает).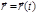 частицы массой m; требуется найти действующую на частицу силу.
частицы массой m; требуется найти действующую на частицу силу.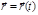 и подстановкой полученного выражения
и подстановкой полученного выражения  в основное уравнение динамики. В результате получаем некоторую функциональную зависимость
в основное уравнение динамики. В результате получаем некоторую функциональную зависимость  . Используя уравнения
. Используя уравнения 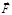 в различных точках пространства, т. е. определить вид силового поля. Прямая задача динамики сравнительно простая, требует применения методов только дифференциального исчисления и всегда имеет решение.
в различных точках пространства, т. е. определить вид силового поля. Прямая задача динамики сравнительно простая, требует применения методов только дифференциального исчисления и всегда имеет решение. , т. е. известны проекции
, т. е. известны проекции 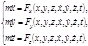 (1.7.2)
(1.7.2)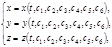 (1.7.3)
(1.7.3)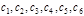 – произвольные постоянные. В простейших случаях переменные в уравнениях (1.7.2) разделяются, и решение сводится к последовательному взятию двух неопределенных интегралов (квадратурам). Поэтому общее решение иногда называют интегралом уравнений, хотя в общем случае решение к квадратурам не сводится.
– произвольные постоянные. В простейших случаях переменные в уравнениях (1.7.2) разделяются, и решение сводится к последовательному взятию двух неопределенных интегралов (квадратурам). Поэтому общее решение иногда называют интегралом уравнений, хотя в общем случае решение к квадратурам не сводится. одно и то же для всех случаев. Таким образом, задание силы не определяет однозначно движение частицы: под действием одной и той же силы частица может совершать любые движения из семейства, описанного формулами (1.7.3). Чтобы обратная задача динамики имела определенное решение, необходимы добавочные начальные условия, например:
одно и то же для всех случаев. Таким образом, задание силы не определяет однозначно движение частицы: под действием одной и той же силы частица может совершать любые движения из семейства, описанного формулами (1.7.3). Чтобы обратная задача динамики имела определенное решение, необходимы добавочные начальные условия, например: 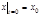 ,
, 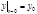 ,
, 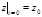 ,
, 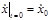 ,
,  ,
, 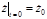 . Положив в (1.7.3) t = 0 и используя начальные условия, получаем:
. Положив в (1.7.3) t = 0 и используя начальные условия, получаем: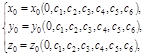 (1.7.4)
(1.7.4)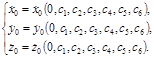 (1.7.5)
(1.7.5)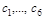 через начальные координаты и скорости:
через начальные координаты и скорости:  и т. д. Подстановка найденных значений
и т. д. Подстановка найденных значений 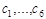 в общее решение (1.7.3) дает частное решение системы дифференциальных уравнений (1.7.2). Это и есть искомые кинематические уравнения движения частицы:
в общее решение (1.7.3) дает частное решение системы дифференциальных уравнений (1.7.2). Это и есть искомые кинематические уравнения движения частицы: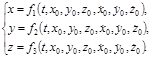 (1.7.6)
(1.7.6)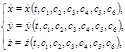 (1.7.7)
(1.7.7)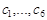 . Предположим, что эта система решена:
. Предположим, что эта система решена: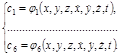 (1.7.8)
(1.7.8)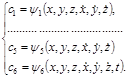 (1.7.9)
(1.7.9)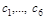 – постоянные, то функции
– постоянные, то функции 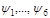 сохраняют свои значения при движении частицы. Они называются первыми интегралами движения и выражают законы сохранения некоторых величин с. Из (1.7.9) следует существование шести независимых первых интегралов. Любая функция первых интегралов также интеграл движения (зависимый). Если все шесть первых интегралов известны, то из них можно без интегрирования получить полное решение второй задачи динамики. Знание одного первого интеграла позволяет упростить решение исходной системы дифференциальных уравнений.
сохраняют свои значения при движении частицы. Они называются первыми интегралами движения и выражают законы сохранения некоторых величин с. Из (1.7.9) следует существование шести независимых первых интегралов. Любая функция первых интегралов также интеграл движения (зависимый). Если все шесть первых интегралов известны, то из них можно без интегрирования получить полное решение второй задачи динамики. Знание одного первого интеграла позволяет упростить решение исходной системы дифференциальных уравнений.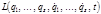 , причем из всех движений, переводящих систему из одного состояния в момент времени
, причем из всех движений, переводящих систему из одного состояния в момент времени 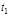 в другое в момент времени
в другое в момент времени 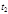 , в действительности осуществляется то, для которого обращается в нуль вариация интеграла
, в действительности осуществляется то, для которого обращается в нуль вариация интеграла (2.5.1) т. е.
(2.5.1) т. е.  (2.5.2)
(2.5.2)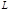 называется функцией Лагранжа, а интеграл
называется функцией Лагранжа, а интеграл 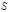 – действием. Обращение в нуль вариации действия есть необходимое условие его экстремума, чем и объясняется название принципа.
– действием. Обращение в нуль вариации действия есть необходимое условие его экстремума, чем и объясняется название принципа. , т. е. на действительных траекториях в пространстве конфигураций имеет место минимум действия. Поэтому сформулированный выше принцип экстремального действия (принцип Гамильтона-Остроградского) называют в данном случае принципом минимального действия.
, т. е. на действительных траекториях в пространстве конфигураций имеет место минимум действия. Поэтому сформулированный выше принцип экстремального действия (принцип Гамильтона-Остроградского) называют в данном случае принципом минимального действия.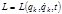 , где
, где 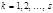 , поэтому получаются дифференциальные уравнения для обобщенных координат, т. е. уравнения движения.
, поэтому получаются дифференциальные уравнения для обобщенных координат, т. е. уравнения движения.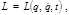 (2.5.3)
(2.5.3)
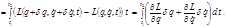 (2.5.4)
(2.5.4)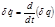 , что и подставляем в (2.5.4):
, что и подставляем в (2.5.4):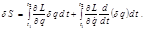 (2.5.5)
(2.5.5)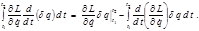 (2.5.6)
(2.5.6) , для которой
, для которой 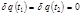 (первое и второе состояния точно определены). Тогда
(первое и второе состояния точно определены). Тогда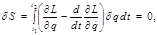 (2.5.7)
(2.5.7)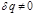 . Поэтому
. Поэтому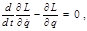 (2.5.8)
(2.5.8) частиц с
частиц с 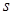 степенями свободы несложно:
степенями свободы несложно: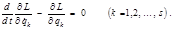 (2.5.9)
(2.5.9) уравнения движения (2.5.9) также инвариантны по отношению к этим преобразованиям.
уравнения движения (2.5.9) также инвариантны по отношению к этим преобразованиям.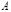 и
и  , каждая из которых, будучи замкнутой, имела бы функции Лагранжа
, каждая из которых, будучи замкнутой, имела бы функции Лагранжа 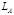 и
и 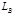 соответственно. Тогда при разведении частей так далеко, что взаимодействием между ними можно пренебречь, лагранжиан системы в целом стремится к пределу
соответственно. Тогда при разведении частей так далеко, что взаимодействием между ними можно пренебречь, лагранжиан системы в целом стремится к пределу  (2.5.10)
(2.5.10)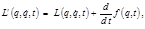 (2.5.11), то
(2.5.11), то (2.5.12)
(2.5.12) , и если
, и если  , то и
, то и  . Вид уравнений движения остается неизменным.
. Вид уравнений движения остается неизменным.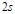 величин
величин  и
и 
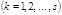 , определяющих ее состояние, изменяются со временем. Но существуют функции этих величин, сохраняющие при движении системы постоянные значения, зависящие только от начальных условий. Эти функции называют интегралами движения. Динамические уравнения механики, основанные на законах Ньютона, приводят к первым интегралам движения или к законам сохранения энергии, импульса и момента импульса. Уравнения Лагранжа, описывающие движение системы в обобщенных координатах, также приводят к сохранению некоторых величин, носящих название обобщенной энергии и обобщенных импульсов.
, определяющих ее состояние, изменяются со временем. Но существуют функции этих величин, сохраняющие при движении системы постоянные значения, зависящие только от начальных условий. Эти функции называют интегралами движения. Динамические уравнения механики, основанные на законах Ньютона, приводят к первым интегралам движения или к законам сохранения энергии, импульса и момента импульса. Уравнения Лагранжа, описывающие движение системы в обобщенных координатах, также приводят к сохранению некоторых величин, носящих название обобщенной энергии и обобщенных импульсов.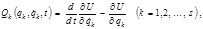 (3.1.1.)
(3.1.1.) – обобщенный потенциал. Уравнения Лагранжа в этом случае имеет вид:
– обобщенный потенциал. Уравнения Лагранжа в этом случае имеет вид: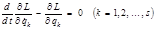 (3.1.2)
(3.1.2) . (3.1.3)
. (3.1.3)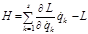 (3.1.4)
(3.1.4)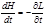 . (3.1.5)
. (3.1.5)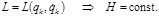 (3.1.6)
(3.1.6) (3.1.7)
(3.1.7)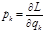 (3.1.8)
(3.1.8)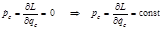 . (3.1.9)
. (3.1.9) и
и 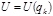 имеем
имеем  , и вид уравнений Лагранжа простой:
, и вид уравнений Лагранжа простой:  , (3.1.10) где
, (3.1.10) где 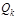 – обобщенная сила.
– обобщенная сила. и в декартовых координатах. В самом деле, если
и в декартовых координатах. В самом деле, если 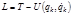 , то
, то 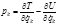 ; в декартовых координатах
; в декартовых координатах  , а в векторной форме записи имеем:
, а в векторной форме записи имеем: 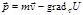 . Таким образом, в поле обобщенно-потенциальных сил может сохраняться та или иная составляющая не обычного, а обобщенного импульса, при условии равенства нулю соответствующей проекции силы. Обобщенный импульс совпадает с обычным только тогда, когда обобщенный потенциал совпадает с потенциальной энергией.
. Таким образом, в поле обобщенно-потенциальных сил может сохраняться та или иная составляющая не обычного, а обобщенного импульса, при условии равенства нулю соответствующей проекции силы. Обобщенный импульс совпадает с обычным только тогда, когда обобщенный потенциал совпадает с потенциальной энергией. , где
, где  . Найдем траекторию частицы массой
. Найдем траекторию частицы массой 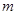 в таком поле в дифференциальной и интегральной формах.
в таком поле в дифференциальной и интегральной формах.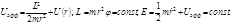 (4.3.1)
(4.3.1)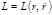 можно представить в виде:
можно представить в виде:  (4.3.2)
(4.3.2) и обобщенной скоростью
и обобщенной скоростью 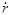 в поле с потенциалом
в поле с потенциалом 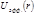 . Подставляя (4.3.2) в уравнение Лагранжа, получаем:
. Подставляя (4.3.2) в уравнение Лагранжа, получаем: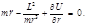 (4.3.3)
(4.3.3) по времени (учитывая, что
по времени (учитывая, что 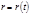 ). Учтем далее, что
). Учтем далее, что  и
и 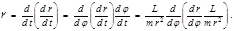 (4.3.4)
(4.3.4)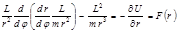 (4.3.5) или
(4.3.5) или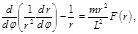 (4.3.6)
(4.3.6)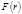 – проекция силы
– проекция силы  на направление
на направление 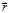 . Обозначим
. Обозначим 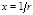 . При этом
. При этом 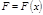 и
и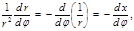 (4.3.7)
(4.3.7) 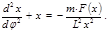 (4.3.8)
(4.3.8) , то
, то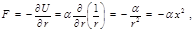 (4.3.9)
(4.3.9)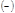 показывает, что это сила притяжения. Дифференциальное уравнение траектории в поле притяжения кулоновского типа:
показывает, что это сила притяжения. Дифференциальное уравнение траектории в поле притяжения кулоновского типа: (4.3.10)
(4.3.10)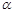 зависит от масс (зарядов) тел и выбора системы единиц.
зависит от масс (зарядов) тел и выбора системы единиц.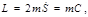 (4.3.11)
(4.3.11)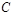 – удвоенная секториальная скорость, для любого поля притяжения кулоновского типа имеем:
– удвоенная секториальная скорость, для любого поля притяжения кулоновского типа имеем: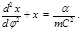 (4.3.12)
(4.3.12)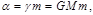 (4.3.13)
(4.3.13)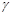 – гауссова постоянная,
– гауссова постоянная,  – постоянная тяготения,
– постоянная тяготения, 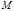 – масса тела, в поле тяготения которого движется частица массой
– масса тела, в поле тяготения которого движется частица массой 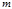 (тело
(тело 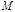 неподвижно).
неподвижно).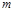 и
и 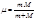 , расстояние которой от центра инерции
, расстояние которой от центра инерции 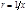 . Уравнение траектории этой точки
. Уравнение траектории этой точки  (4.3.14) или
(4.3.14) или 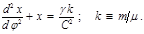 (4.3.15)
(4.3.15) (4.3.16)
(4.3.16)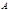 и
и 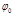 – произвольные постоянные,
– произвольные постоянные, 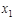 – общее решение соответствующего (4.3.15) однородного уравнения,
– общее решение соответствующего (4.3.15) однородного уравнения, 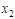 – частное решение (4.3.15). Тогда
– частное решение (4.3.15). Тогда 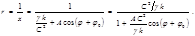 (4.3.17)
(4.3.17)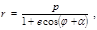 (4.3.18)
(4.3.18)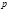 – параметр кривой,
– параметр кривой,  – эксцентриситет. Итак, в поле тяготения (в поле притяжения кулоновского типа) частица (или изображающая точка для замкнутой системы двух частиц) движется по траектории, представляющей собой одно из конических сечений. В нашем случае
– эксцентриситет. Итак, в поле тяготения (в поле притяжения кулоновского типа) частица (или изображающая точка для замкнутой системы двух частиц) движется по траектории, представляющей собой одно из конических сечений. В нашем случае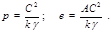 (4.3.19)
(4.3.19) и
и 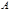 , причем
, причем  , а полная энергия
, а полная энергия  определяет величину
определяет величину 


