
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тензоры деформации и скоростей деформацииСодержание книги
Поиск на нашем сайте Рассмотрим деформацию малой частицы сплошной среды, имеющей первоначально шаровую форму. Деформация определяется вектором
т. е. если до деформации радиус-вектор точки был
Эти формулы несложно вывести, зная f. Т. к. деформации малые, то соответствующие относительные координаты до и после деформации отличаются незначительно. Тогда
Таким образом, если точки малой частицы сплошной среды располагались сначала на сфере радиусом А, уравнение которой
то после деформации они перейдут на поверхность второго порядка, уравнение которой (с точностью до членов второго порядка малости) запишется в виде:
Это так называемый эллипсоид деформации. Если оси координат совпадают с осями этого эллипсоида (с главными осями эллипсоида деформации), то (8.3.6) принимает вид:
где Вектор деформации Рассмотрим движение сплошной среды с точки зрения переменных Эйлера и выразим через них компоненты деформации. Для малых деформаций
а для сдвигов запишем:
Таким образом, все компоненты деформации – функции координат x, y, z точек пространства. Покажем, как изменяются эти компоненты при изменении СК xyz на СК
Вводя обозначения:
Величины Ф, зависящие от x, y, z и удовлетворяющие (8.3.13), образуют афинный ортогональный тензор второго ранга – тензор деформации:
Этот тензор в каждой точке пространства характеризует деформацию сплошной среды, окружающей данную точку. Если
Если смещение точки малой частицы
Величины
Закон сохранения массы и уравнение непрерывности Важная характеристика сплошной среды – ее плотность. Выделим в среде малый объем
Это определение имеет смысл только для сплошной среды. Последнее накладывает ограничения на перемещения и плотности точек среды, а в случае конечных перемещений - на скорости точек среды. Используя переменные Лагранжа, запишем условие того, что выделенный объем V сплошной среды в начальный момент
Для малых перемещений
и из (8.4.2) и (8.4.3) следует:
и, поскольку выбранный объем произволен, то
Это уравнение непрерывности в переменных Лагранжа или переменных Эйлера. Собственно, уравнение непрерывности в переменных Лагранжа – (8.4.7). Равенство (8.4.8) представляет собой выражение для относительного объемного расширения
Это равенство связывает плотность в двух точках пространства Разделив последнее равенство на
Уравнение непрерывности в переменных Эйлера:
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , (8.3.1)
, (8.3.1) , то после деформации
, то после деформации  . Относительные координаты точки до деформации
. Относительные координаты точки до деформации  , а после деформации
, а после деформации (8.3.2)
(8.3.2) (8.3.3) и
(8.3.3) и 8.3.4)
8.3.4) , (8.3.5)
, (8.3.5) (8.3.6)
(8.3.6) (8.3.7)
(8.3.7)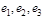 – относительные удлинения отрезков, параллельных осям новой СК. Новые оси замечательны тем, что смещения частиц, расположенных первоначально на этих осях, происходят только вдоль этих осей, т. е. точки на главных осях до деформации остаются на этих осях и после деформации.
– относительные удлинения отрезков, параллельных осям новой СК. Новые оси замечательны тем, что смещения частиц, расположенных первоначально на этих осях, происходят только вдоль этих осей, т. е. точки на главных осях до деформации остаются на этих осях и после деформации. определяется шестью компонентами деформации, которые записаны в переменных Лагранжа.
определяется шестью компонентами деформации, которые записаны в переменных Лагранжа. ,
,  ,
,  .Относительные удлинения:
.Относительные удлинения: (8.3.8)
(8.3.8) (8.3.9)
(8.3.9) . Учитывая, что
. Учитывая, что (8.3.10) и используя то, что скалярное произведение
(8.3.10) и используя то, что скалярное произведение (8.3.11) не зависит от выбора СК, можно получить:
(8.3.11) не зависит от выбора СК, можно получить: . (8.3.12)
. (8.3.12) ,
,  ,
, 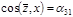 и т. д.; а также
и т. д.; а также  ,
,  ,
,  ,
,  ,
,  ,
,  , можно представить формулы преобразований координат в виде:
, можно представить формулы преобразований координат в виде: (l, k = 1, 2, 3). (8.3.13)
(l, k = 1, 2, 3). (8.3.13) . (8.3.14)
. (8.3.14) выбраны вдоль главных осей деформации, то тензор диагональный:
выбраны вдоль главных осей деформации, то тензор диагональный: . (8.3.15)
. (8.3.15)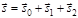 , где
, где  , то для скоростей запишем:
, то для скоростей запишем:  , где
, где  – скорость поступательного движения частицы,
– скорость поступательного движения частицы,  – вращательная скорость частицы относительно начала СК,
– вращательная скорость частицы относительно начала СК,  – скорость деформации. Тогда естественно обозначить:
– скорость деформации. Тогда естественно обозначить:
 (8.3.16) В этом случае
(8.3.16) В этом случае . (8.3.17)
. (8.3.17) – компоненты скоростей деформации. Тогда можно построить тензор скоростей деформации:
– компоненты скоростей деформации. Тогда можно построить тензор скоростей деформации: . (8.3.18)
. (8.3.18) , охватывающий точку, в которой ищется плотность. Если его масса
, охватывающий точку, в которой ищется плотность. Если его масса 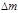 , то плотность
, то плотность . (8.4.1)
. (8.4.1) и в конечный момент
и в конечный момент  имеет одинаковую массу:
имеет одинаковую массу: , (8.4.2) где
, (8.4.2) где  ,
,  ,
,  . Заменяя во втором интеграле переменные Эйлера переменными Лагранжа, получим:
. Заменяя во втором интеграле переменные Эйлера переменными Лагранжа, получим: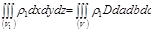 . (8.4.3) Здесь
. (8.4.3) Здесь (8.4.4)
(8.4.4) , (8.4.5)
, (8.4.5) , (8.4.6)
, (8.4.6) (8.4.7)или
(8.4.7)или . (8.4.8)
. (8.4.8) при деформации (при неизменной массе
при деформации (при неизменной массе  и
и  ). Из (8.4.8) вытекает:
). Из (8.4.8) вытекает: . (8.4.9)
. (8.4.9) и
и  , которые точка сплошной среды занимает в моменты времени t и
, которые точка сплошной среды занимает в моменты времени t и  , смещаясь на малый вектор
, смещаясь на малый вектор  .
. и переходя к пределу при
и переходя к пределу при 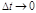 , получим закон сохранения массы (условие неизменности массы выделенного в среде объема; см. подробнее в [1, с. 29]):
, получим закон сохранения массы (условие неизменности массы выделенного в среде объема; см. подробнее в [1, с. 29]): . (8.4.10)
. (8.4.10) . (8.4.11)
. (8.4.11)


