
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамические характеристики частицы. Законы НьютонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основные принципы классической механики были сформулированы в 1687 г. И. Ньютоном в книге «Математические начала натуральной философии». Законы Ньютона в авторской формулировке (перевод А.Н. Крылова): I закон: Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. II закон: Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. III закон: Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны. Дадим законам Ньютона современную трактовку. I закон постулирует существование инерциальной системы отсчета (ИСО), т. е. такой системы отсчета, в которой все изолированные (свободные, не подверженные внешним воздействиям) материальные точки движутся равномерно и прямолинейно (или покоятся). Понятие ИСО – идеализация. В ИСО имеет место явление инерции – равномерное и прямолинейное движение свободного тела (частицы). II закон описывает движение материальной точки относительно ИСО, в том числе и несвободной (подверженной воздействию). Любое физическое тело обладает инертностью – свойством препятствовать изменению его скорости относительно ИСО. Мера инертности – масса. В классической механике масса – аддитивная величина (масса тела равна сумме масс его частей). Величина, определяемая произведением массы тела на его скорость – импульс (количество движения):
Импульс свободной частицы в ИСО не изменяется с течением времени (сохраняется), т. к. свободная частица движется по инерции, а масса частицы в классической механике неизменна. Для изменения импульса частицы в ИСО необходимо воздействие на нее других материальных объектов. Такое воздействие характеризуется векторной физической величиной – силой. Чем больше сила, тем быстрее изменяется импульс частицы в ИСО. Современная формулировка II закона: производная импульса материальной точки по времени равна силе, действующей на материальную точку в ИСО:
При
Тогда II закон Ньютона можно переформулировать: ускорение материальной точки относительно ИСО прямо пропорционально действующей силе и обратно пропорционально массе. В соответствующей системе единиц
Заметим, что с помощью (1.5.4) можно определить силу и массу независимо друг от друга, задавая эталоны этих величин и измеряя ускорения кинематически. В I и II законах говорится об одном отдельно взятом теле (частице); воздействие на него других тел рассматривается без анализа последствий этого воздействия для последних. В III законе рассматривается система из двух тел: силы, с которыми две материальные точки действуют друг на друга, равны по модулю и направлены в противоположные стороны по прямой, проходящей через эти точки:
Дополнением к законам Ньютона служит принцип суперпозиции сил: ускорение, получаемое частицей при одновременном действии на нее нескольких сил, определяется геометрической суммой ускорений, получаемых частицей при действии каждой из этих сил в отдельности:
Если речь идет об одной частице, подверженной действию нескольких сил, то величина
называется равнодействующей силой. В этом случае под «силой» в форму-лировке II закона Ньютона следует понимать именно равнодействующую силу. Заметим, что при
Принцип относительности Галилея. Механическая концепция Взаимодействия Обратимся к преобразованиям Галилея для координат и скоростей. Легко видеть, что частица, движущаяся в СК 01 XYZ с постоянной скоростью Оказывается, что все ИСО эквивалентны и физически. В классической механике постулируется, что все ИСО эквивалентны для механических взаимодействий. Это утверждает принцип относительности Галилея, суть которого в том, что любой механический процесс происходит во всех ИСО по одним и тем же законам, имеющим инвариантную форму. Имеются также неизменные величины – инварианты преобразований Галилея (ускорение, масса, сила). Они особенно существенны при изучении движения, т. к. выражают одинаковые во всех ИСО свойства тел и движений. II закон Ньютона не только сохраняет свою форму во всех ИСО, но и связывает инвариантные величины. III закон Ньютона и принцип независимого действия сил также справедливы во всех ИСО. В классической механике все ИСО равноправны, привилегированной или абсолютно неподвижной системы отсчета нет. Остановимся подробнее на концепциях взаимодействия в механике. Заметим, что изучение природы сил не входит в задачи механики и выполняется в других разделах физики. По данному вопросу можно высказать лишь самые общие соображения, вытекающие из моделей материальных объектов и взаимодействий между ними, принятых в механике. Исходной для механики является система материальных точек в пустоте, связанных мгновенно передающимся взаимодействием. Силы взаимодействия между любыми двумя частицами центральные и подчиняются III закону Ньютона. Силы, действующие на частицу со стороны других частиц, могут зависеть от относительных расстояний, а эти расстояния – от положения рассматриваемой частицы в пространстве. Поэтому равнодействующая сила – функция координат частицы, а также времени, поскольку частицы могут двигаться:
К механическим силам относят также контактные силы (упругости и трения), возникающие при соприкосновении макроскопических тел. Задача о подробном рассмотрении взаимодействия на уровне микрочастиц в механике не ставится, а рассматривается и эмпирически определяется суммарный макроскопический эффект. Для двух тел, взаимодействующих посредством контактных сил, справедлив III закон Ньютона. В рамки механической концепции укладываются основные известные проявления гравитационного взаимодействия и частично электромагнитного. Сильное и слабое взаимодействия не соответствуют механической концепции в главном: для них исключено применение модели дальнодействия. Однако, математическая концепция, несмотря на привлекательную математическую простоту, не может быть положена в основу физической картины всего материального мира. Главный ее недостаток – отсутствие в системе материальных тел материальных полей, взаимодействующих с телами. Поля передают взаимодействие между телами с большой, но не бесконечной скоростью, действуя на частицу там, где она находится в поле (близкодействие). Рассмотрим последствия включения поля в механическую систему. Поле непрерывно заполняет пространство. Основное его механическое действие силовое: частицы в поле приобретают ускорения. Для сил, действующих в физических полях на частицы, справедлив II закон Ньютона, если движение частицы не изменяет существенно параметры поля и частицей (материальной точкой) моделируется физическое макроскопическое тело. Взаимодействие от частицы к частице передается с конечной скоростью с за время Движение макроскопических тел с нерелятивистскими скоростями происходит в сравнительно слабых и медленно изменяющихся полях (гравитационном и электромагнитном), поэтому данное движение можно изучать в механике без применения понятия материального поля. В физике же микромира механическая концепция взаимодействия не применима из-за возможности существования нецентральных сил взаимодействия между частицами, из-за релятивистских скоростей, из-за взаимопревращений частиц и т. д.
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.008 с.) |

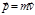 . (1.5.1)
. (1.5.1)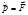 . (1.5.2)
. (1.5.2)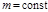 из (1.5.2) имеем:
из (1.5.2) имеем: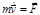 или
или 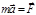 .(1.5.3)
.(1.5.3)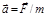 . (1.5.4)
. (1.5.4)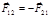 . (1.5.5)
. (1.5.5)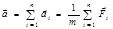 . (1.5.6)
. (1.5.6)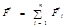 (1.5.7)
(1.5.7)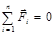 ускорение тела
ускорение тела  , т. е. в ИСО тело ведет себя как свободное, хотя таковым не является. Поэтому недопустимо трактовать I закон Ньютона как следствие II закона: I закон постулирует существование ИСО, а II закон определяет характер движения тела в ИСО.
, т. е. в ИСО тело ведет себя как свободное, хотя таковым не является. Поэтому недопустимо трактовать I закон Ньютона как следствие II закона: I закон постулирует существование ИСО, а II закон определяет характер движения тела в ИСО. , в СК 0 xyz также движется с постоянной скоростью
, в СК 0 xyz также движется с постоянной скоростью  , хотя и иной по величине. Следовательно, если одна из систем отсчета инерциальная, то и любая другая, движущаяся относительно нее равномерно, прямолинейно и поступательно, также инерциальная. Свойства симметрии пространства и времени, постулированные для одной из ИСО справедливы для пространства и времени в любой другой ИСО, в силу линейности преобразований Галилея. Все ИСО геометрически эквивалентны.
, хотя и иной по величине. Следовательно, если одна из систем отсчета инерциальная, то и любая другая, движущаяся относительно нее равномерно, прямолинейно и поступательно, также инерциальная. Свойства симметрии пространства и времени, постулированные для одной из ИСО справедливы для пространства и времени в любой другой ИСО, в силу линейности преобразований Галилея. Все ИСО геометрически эквивалентны. . Таким образом, мы приходим к понятию силового поля – области пространства, в каждой точке которого на частицу действует сила, зависящая от координат и времени. Такое понятие силового поля полностью согласуется с механической моделью материальных объектов и концепцией взаимодействия. Но такое поле не материальный объект, входящий в механическую систему, а просто удобное вспомогательное математическое понятие, позволяющее вместо подробного рассмотрения всех попарных взаимодействий использовать выражение вида
. Таким образом, мы приходим к понятию силового поля – области пространства, в каждой точке которого на частицу действует сила, зависящая от координат и времени. Такое понятие силового поля полностью согласуется с механической моделью материальных объектов и концепцией взаимодействия. Но такое поле не материальный объект, входящий в механическую систему, а просто удобное вспомогательное математическое понятие, позволяющее вместо подробного рассмотрения всех попарных взаимодействий использовать выражение вида  . В рамках рассматриваемой механической концепции равнодействующая сила может быть также функцией скорости данной частицы, поэтому в общем случае
. В рамках рассматриваемой механической концепции равнодействующая сила может быть также функцией скорости данной частицы, поэтому в общем случае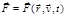 . (1.6.1)
. (1.6.1)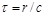 (время запаздывания), что нарушает равенство действия и противодействия – III закон Ньютона не выполняется. В чистом виде основная механическая модель (система частиц и дальнодействие) может применяться, если материальное поле можно заменить силовым, а последнее правомерно, если временем запаздывания можно пренебречь (т. е. при скорости частицы
(время запаздывания), что нарушает равенство действия и противодействия – III закон Ньютона не выполняется. В чистом виде основная механическая модель (система частиц и дальнодействие) может применяться, если материальное поле можно заменить силовым, а последнее правомерно, если временем запаздывания можно пренебречь (т. е. при скорости частицы 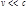 ). Кроме того, поле должно изменяться сравнительно медленно, чтобы во время запаздывания его можно было бы считать стационарным.
). Кроме того, поле должно изменяться сравнительно медленно, чтобы во время запаздывания его можно было бы считать стационарным.


