
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщенные координаты и обобщенные силыСодержание книги
Поиск на нашем сайте
Как уже отмечалось, механическая система из Выберем
Т. к. несвободные координаты – однозначные функции свободных, то они также однозначные функции параметров Выбор обобщенных координат может осуществляться разными способами. Пусть, например, частица движется по окружности радиусом Пространство, образованное совокупностью обобщенных координат Обратимся к принципу виртуальных перемещений (условие Лагранжа (2.2.20)):
В отсутствие связей вариации всех координат независимы, и из (2.3.2) непосредственно следуют условия равновесия системы:
Если имеются идеальные связи, то (2.3.2) по-прежнему имеет место, но из него в общем случае условия равновесия (2.3.3) не следуют, т. к. не все вариации координат независимы, и поэтому не все коэффициенты при вариациях в (2.3.2) обращаются в нуль. Например, для частицы, перемещающейся равномерно и прямолинейно по горизонтальной плоскости (или покоящейся, т. е. в обоих случаях находящейся в равновесии) имеет место условие Лагранжа Для получения уравнений равновесия системы с идеальными связями из принципа виртуальных перемещений (из условия Лагранжа) используют метод обобщенных координат. Выбираем обобщенные координаты
Вариации обобщенных координат независимы. Подставляя (2.3.4) в (2.3.2) и изменяя порядок суммирования, получаем:
Коэффициенты при вариациях обобщенных координат – обобщенные силы:
Принцип виртуальных перемещений в обобщенных координатах:
Поскольку величины
Известно, что консервативное силовое поле (работа сил которого по перемещению частицы не зависит от формы траектории последней, а сами силы зависят только от координат частицы) характеризуется потенциалом:
Частица в таком поле обладает потенциальной энергией
Потенциальная энергия системы частиц
силы связаны с потенциальной энергией соотношениями:
В обобщенных координатах
Тогда
Если Сделаем несколько замечаний по поводу использованного выше понятия потенциальной энергии, поскольку в различных пособиях это понятие вводится и трактуется по-разному. Механической энергией называют величину, характеризующую способность тела (или системы) совершать механическую работу. Другими словами, если два различных состояния тела характеризуются однородными величинами Используя второй закон Ньютона для частицы, запишем:
где
Кинетическая энергия тела (системы тел) зависит от выбора системы отсчета. Кинетическая энергия системы тел подчиняется теореме Кёнига и может быть представлена в виде суммы кинетической энергии системы как целого с массой, сосредоточенной в центре масс и движущейся вместе с ним, и суммарной кинетической энергии всех тел системы в системе отсчета, связанной с центром масс. Перейдем к понятию потенциальной энергии. Пусть на частицу действует сила
Отсюда
Легко видеть, что в общем случае Если же поле нестационарное, или если силы зависят от скорости (даже если они гироскопические, т. е. перпендикулярные направлению перемещения в каждой точке траектории, например, сила Лоренца), то говорить о потенциальной энергии не приходится. Для поля консервативных сил
откуда следует:
Это закон сохранения полной механической энергии 9 Уравнения Лагранжа (второго рода) Как отмечалось выше, задача о движении механической системы из Метод обобщенных координат позволяет заменить систему Для механической системы с идеальными связями задача математически заключается в преобразовании к обобщенным координатам
Используя соотношения (2.3.1), выражающие декартовы координаты частиц системы через обобщенные координаты, а также понятие обобщенной силы (2.3.6), из (2.4.1) с помощью довольно громоздких преобразований (см. подробнее в [4, с. 181–182]) получим
где
Это и есть искомые уравнения Лагранжа. Для их составления необходимо знать выражение для кинетической энергии системы частиц в выбранных обобщенных координатах и значения обобщенных сил. Каждой обобщенной координате соответствует свое уравнение Лагранжа. Особый интерес представляют уравнения Лагранжа, описывающие движение системы частиц с обобщенно-потенциальными силами. Сила называется обобщенно-потенциальной, если она зависит от обобщенных координат, обобщенных скоростей, времени и удовлетворяет условию:
где
где Итак, для составления уравнений Лагранжа в случае обобщенно-потен-циальных сил достаточно знать выражение для лагранжиана системы частиц. При этом уравнения (2.4.6) инвариантны по отношению к выбору системы отсчета. Лагранжиан задается неоднозначно: добавление к нему любой величины, не зависящей явно от При наличии диссипативных сил уравнения Лагранжа принимают вид:
Заметим, что если диссипативные силы линейно зависят от скоростей частиц, то они могут быть выражены (см. подробнее в []) через скалярную функцию:
где
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.43.27 (0.006 с.) |

 частиц, на которую наложены
частиц, на которую наложены 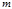 связей, имеет
связей, имеет  степеней свободы. Этим степеням свободы соответствуют
степеней свободы. Этим степеням свободы соответствуют  так называемых свободных координат. Остальные
так называемых свободных координат. Остальные  координат могут быть выражены как однозначные функции свободных координат.
координат могут быть выражены как однозначные функции свободных координат. независимых параметров
независимых параметров  так, чтобы свободные координаты были их однозначными функциями:
так, чтобы свободные координаты были их однозначными функциями: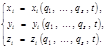 (2.3.1)
(2.3.1)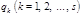 и, в общем случае, времени
и, в общем случае, времени  , т. е. все декартовы координаты частиц системы могут быть выражены по формулам преобразования через
, т. е. все декартовы координаты частиц системы могут быть выражены по формулам преобразования через  параметров
параметров 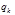 и время
и время  (см. 2.3.1). При этом уравнения связей удовлетворяются тождественно. Параметры
(см. 2.3.1). При этом уравнения связей удовлетворяются тождественно. Параметры  называют обобщенными координатами механической системы. Время
называют обобщенными координатами механической системы. Время 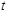 входит в (2.3.1), если связи нестационарные.
входит в (2.3.1), если связи нестационарные. в плоскости
в плоскости  . Тогда уравнение связей:
. Тогда уравнение связей:  и
и  ; здесь одна степень свободы. Логично в качестве обобщенной координаты выбрать угловую:
; здесь одна степень свободы. Логично в качестве обобщенной координаты выбрать угловую: 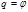 . При этом
. При этом  . Если известна сила, действующая на частицу, то можно составить динамическое уравнение движения для координаты
. Если известна сила, действующая на частицу, то можно составить динамическое уравнение движения для координаты  и найти зависимость
и найти зависимость  .
. в данный момент времени Т. е. вместо
в данный момент времени Т. е. вместо  точек с координатами
точек с координатами 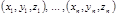 рассматривается одна точка с координатами
рассматривается одна точка с координатами  , причем
, причем  . Задача математически упрощается.
. Задача математически упрощается. (2.3.2)
(2.3.2) (2.3.3)
(2.3.3) , но
, но  , и условие равновесия
, и условие равновесия  вовсе не следует из условия Лагранжа.
вовсе не следует из условия Лагранжа. для данной системы частиц. Декартовы координаты выражаются через обобщенные (и время) в соответствии с (2.3.1). Варьируя (2.3.1), находим:
для данной системы частиц. Декартовы координаты выражаются через обобщенные (и время) в соответствии с (2.3.1). Варьируя (2.3.1), находим:

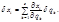 (2.3.4)
(2.3.4) (2.3.5)
(2.3.5) (2.3.6)
(2.3.6) (2.3.7)
(2.3.7) произвольны и независимы, то из (2.3.7) следуют условия равновесия системы частиц:
произвольны и независимы, то из (2.3.7) следуют условия равновесия системы частиц: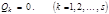 (2.3.8)
(2.3.8)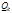 – обобщенное понятие силы в механике. Произведение
– обобщенное понятие силы в механике. Произведение  всегда имеет размерность работы; размерность обобщенной силы
всегда имеет размерность работы; размерность обобщенной силы  зависит от размерности соответствующей обобщенной координаты
зависит от размерности соответствующей обобщенной координаты 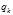 .
. (2.3.9)
(2.3.9) – масса частицы. (2.3.10)
– масса частицы. (2.3.10) (2.3.11)
(2.3.11) (2.3.12)
(2.3.12) (2.3.13)
(2.3.13)
 (2.3.14)
(2.3.14) , то
, то  , т. е. потенциальная энергия
, т. е. потенциальная энергия  в равновесии имеет экстремум.
в равновесии имеет экстремум. и
и  , а разность этих величин равна работе по переводу тела из одного состояния в другое, то сама величина
, а разность этих величин равна работе по переводу тела из одного состояния в другое, то сама величина  имеет смысл энергии. Как известно, элементарная работа определяется скалярным произведением силы на элементарное перемещение:
имеет смысл энергии. Как известно, элементарная работа определяется скалярным произведением силы на элементарное перемещение:  . Здесь знак
. Здесь знак  подчеркивает, что работа не является функцией состояния, и
подчеркивает, что работа не является функцией состояния, и  не является полным дифференциалом.
не является полным дифференциалом. умножая скалярно на
умножая скалярно на  , получаем:
, получаем:  или
или  . Итак, мы получили выражение для известной из курса общей физики теоремы об изменении кинетической энергии (в дифференциальной форме):
. Итак, мы получили выражение для известной из курса общей физики теоремы об изменении кинетической энергии (в дифференциальной форме): (2.3.15)
(2.3.15) – кинетическая энергия, присущая движущемуся телу. Интегральная запись этой теоремы:
– кинетическая энергия, присущая движущемуся телу. Интегральная запись этой теоремы: (2.3.16)
(2.3.16) , удовлетворяющая условию
, удовлетворяющая условию  , где
, где  – потенциальная функция (некоторая функция координат и времени). Полный дифференциал этой функции
– потенциальная функция (некоторая функция координат и времени). Полный дифференциал этой функции (2.3.17)
(2.3.17) (2.3.18)
(2.3.18) , т. е. функция
, т. е. функция 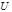 не соответствует определению механической энергии, приведенному выше. Но если
не соответствует определению механической энергии, приведенному выше. Но если  ), то
), то  . В этом случае
. В этом случае  имеет смысл механической энергии и называется потенциальной энергией. В частности, потенциальной энергией обладает тело в поле консервативных сил, зависящих только от координат, работа которых на любом замкнутом участке траектории равна нулю (т.е. не зависит от формы траектории).
имеет смысл механической энергии и называется потенциальной энергией. В частности, потенциальной энергией обладает тело в поле консервативных сил, зависящих только от координат, работа которых на любом замкнутом участке траектории равна нулю (т.е. не зависит от формы траектории). или
или  (2.3.19)
(2.3.19) (2.3.20)
(2.3.20) частиц с
частиц с  скалярных уравнений с
скалярных уравнений с  неизвестными, дополняя которую
неизвестными, дополняя которую  независимыми соотношениями между координатами частиц и реакциями связей, можно получить решаемую систему
независимыми соотношениями между координатами частиц и реакциями связей, можно получить решаемую систему  скалярных уравнений вида (2.1.10) системой
скалярных уравнений вида (2.1.10) системой 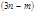 дифференциальных уравнений в независимых обобщенных координатах, не содержащих явно сил реакций
дифференциальных уравнений в независимых обобщенных координатах, не содержащих явно сил реакций  и называемых уравнениями Лагранжа второго рода (или просто уравнениями Лагранжа). Эти уравнения позволяют найти закон движения системы частиц, а затем с помощью (2.1.10) можно определить неизвестные реакции связей. Уравнения Лагранжа имеют инвариантную скалярную форму во всех СК, что позволяет составлять уравнения в наиболее удобной СК, не пользуясь громоздкими формулами перехода.
и называемых уравнениями Лагранжа второго рода (или просто уравнениями Лагранжа). Эти уравнения позволяют найти закон движения системы частиц, а затем с помощью (2.1.10) можно определить неизвестные реакции связей. Уравнения Лагранжа имеют инвариантную скалярную форму во всех СК, что позволяет составлять уравнения в наиболее удобной СК, не пользуясь громоздкими формулами перехода. общего уравнения механики
общего уравнения механики (2.4.1)
(2.4.1) (2.4.2)
(2.4.2) – кинетическая энергия отдельной частицы,
– кинетическая энергия отдельной частицы,  – обобщенные скорости. Кинетическая энергия системы частиц
– обобщенные скорости. Кинетическая энергия системы частиц  , тогда
, тогда (2.4.3) и
(2.4.3) и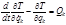 ,
,  . (2.4.4)
. (2.4.4) ,
,  , (2.4.5)
, (2.4.5) – обобщенно-потенциальная функция (обобщенный потенциал). Подставляя (2.4.5) в (2.4.4), находим:
– обобщенно-потенциальная функция (обобщенный потенциал). Подставляя (2.4.5) в (2.4.4), находим: ,
, 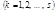 , (2.4.6)
, (2.4.6) – функция Лагранжа (лагранжиан). Уравнения (2.4.6) справедливы также, если
– функция Лагранжа (лагранжиан). Уравнения (2.4.6) справедливы также, если  – потенциальная функция, или если
– потенциальная функция, или если  – потенциальная энергия (частный случай консервативных сил).
– потенциальная энергия (частный случай консервативных сил). , не изменяет уравнений (2.4.6).
, не изменяет уравнений (2.4.6). ,
,  . (2.4.7)
. (2.4.7) (2.4.8)
(2.4.8) – диссипативная функция Рэлея.
– диссипативная функция Рэлея.


