
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип экстремального действия. ПреимуществоСодержание книги
Поиск на нашем сайте
Вариационной концепции Уравнения Лагранжа были получены из уравнений Ньютона для системы частиц с помощью принципа виртуальных перемещений и принципа д¢Аламбера-Лагранжа. Однако уравнения Лагранжа можно получить из общего теоретического принципа экстремального действия, установленного Гамильтоном и обобщенного Остроградским. Этот принцип распространяется не только на механические, но и на квантово-механические системы, а также на поля как системы с бесконечно большим числом степеней свободы. Принцип экстремального действия позволяет получать фундаментальные уравнения физики в различных ее разделах и поэтому имеет важнейшее теоретическое значение. Согласно этому принципу каждая механическая система характеризуется определенной функцией
При этом функция Специальными методами аналитической механики доказывается, что для малых интервалов времени В математике интеграл вида (2.5.1) принадлежит к так называемым функционалам, если рассматривать зависимость его величины от вида подынтегральной функции. Задача об экстремуме функционала (отыскание функции, при которой имеет место экстремум) решается методами вариационного исчисления. В результате находятся дифференциальные уравнения, выполняющиеся для подынтегральной функции. В нашем случае Рассмотрим сначала одномерную задачу:
Изменяя последовательность дифференцирования и варьирования (время не варьируется), получаем
Второй интеграл берется по частям:
Первое слагаемое (2.5.6) обращается в нуль, т. к. по определению ищется функция
причем это должно выполняться при любых
а это и есть уравнение Лагранжа для обобщенно-потенциальных сил. Обобщить (2.5.8) на систему
Особенность принципа экстремального действия – простая его связь с преобразованиями от одной системы отсчета к другой. Если действие является инвариантом некоторых преобразований, то получаемые из соответствующей функции Пусть механическая система состоит из двух частей Это свойство аддитивности функции Лагранжа говорит о том, что уравнения движения каждой из невзаимодействующих частей не могут содержать величины, относящиеся к другим частям системы. Очевидно, умножение функции Лагранжа на произвольную постоянную не отражается на уравнениях движения описываемой ею системы частиц. Свойство аддитивности допускает лишь одновременное умножение лагранжевых функций всех рассматриваемых систем на одинаковую постоянную, что сводится к естественному произволу в выборе единиц измерения для Функция Лагранжа определяется с точностью до прибавления к ней полной производной от любой функции координат и времени. В самом деле, если
Тогда Построение классической механики как физической теории возможно на различных исходных положениях и принципах. Такие принципы могут различаться по своей общности и математической форме, хотя и связаны между собой. Каждая из схем построения механики содержит некоторую новую точку зрения на описание механического движения. Это имеет большую эвристическую ценность: особенности механического движения, остающиеся скрытыми при одних исходных принципах, выступают явно при использовании других.
По математической форме принципы выражаются дифференциальными или интегральными соотношениями. Дифференциальными называют такие законы, формулы которых связывают значения величин, относящиеся к одному и тому же моменту времени или к одной и той же точке пространства. Формулы интегральных законов устанавливают связь между величинами, относящимися к конечному промежутку времени или к конечной области пространства. Принципы механики подразделяются ещё на вариационные и невариационные. Невариационные законы устанавливают соотношения между величинами, имеющими место для действительного движения. Вариационные устанавливают признаки, отличающие действительное движение от всех других кинематически возможных движений. Примеры вариационных дифференциальных принципов: принцип виртуальных перемещений, принцип д¢Аламбера-Лагранжа (общее уравнение механики). Известны интегральные вариационные принципы, обладающие той или иной степенью общности (наиболее общий – принцип Гамильтона-Остроградского). Схема построения классической механики, основанная на законах Ньютона, из которых следует все содержание положений и выводов механики, имеет отличительную черту: подход к силе как к причине изменения механического состояния (такой подход в известной мере нагляден). Другая схема имеет в своей основе интегральный вариационный принцип Гамильтона-Остроградского. В физическом плане она более формальна, но зато и более общая, т. к. распространяется за пределы классической механики. Исходные понятия здесь – лагранжиан и действие; они весьма абстрактны. Принцип экстремального действия находит применение в различных разделах теоретической физики, что связано с методом обобщенных координат, благодаря которому уравнения Лагранжа не ограничены евклидовым пространством. Переход к бесконечномерному пространству конфигураций позволяет применять принцип экстремального действия к системам с бесконечно большим числом степеней свободы – физическим полям. Подчеркнем, что в первой схеме построения механики должны быть заданы силы, во второй – функция Лагранжа (или, как будет показано ниже, функция Гамильтона). Конкретные формулы как для сил, так и для указанных функций, в механике не выводятся, а задаются.
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.108 (0.009 с.) |

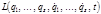 , причем из всех движений, переводящих систему из одного состояния в момент времени
, причем из всех движений, переводящих систему из одного состояния в момент времени 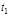 в другое в момент времени
в другое в момент времени 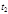 , в действительности осуществляется то, для которого обращается в нуль вариация интеграла
, в действительности осуществляется то, для которого обращается в нуль вариация интеграла (2.5.1) т. е.
(2.5.1) т. е.  (2.5.2)
(2.5.2)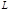 называется функцией Лагранжа, а интеграл
называется функцией Лагранжа, а интеграл 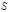 – действием. Обращение в нуль вариации действия есть необходимое условие его экстремума, чем и объясняется название принципа.
– действием. Обращение в нуль вариации действия есть необходимое условие его экстремума, чем и объясняется название принципа. , т. е. на действительных траекториях в пространстве конфигураций имеет место минимум действия. Поэтому сформулированный выше принцип экстремального действия (принцип Гамильтона-Остроградского) называют в данном случае принципом минимального действия.
, т. е. на действительных траекториях в пространстве конфигураций имеет место минимум действия. Поэтому сформулированный выше принцип экстремального действия (принцип Гамильтона-Остроградского) называют в данном случае принципом минимального действия.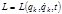 , где
, где 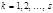 , поэтому получаются дифференциальные уравнения для обобщенных координат, т. е. уравнения движения.
, поэтому получаются дифференциальные уравнения для обобщенных координат, т. е. уравнения движения.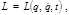 (2.5.3)
(2.5.3)
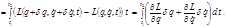 (2.5.4)
(2.5.4)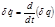 , что и подставляем в (2.5.4):
, что и подставляем в (2.5.4):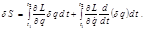 (2.5.5)
(2.5.5)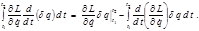 (2.5.6)
(2.5.6) , для которой
, для которой 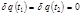 (первое и второе состояния точно определены). Тогда
(первое и второе состояния точно определены). Тогда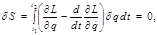 (2.5.7)
(2.5.7)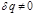 . Поэтому
. Поэтому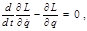 (2.5.8)
(2.5.8) частиц с
частиц с 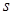 степенями свободы несложно:
степенями свободы несложно: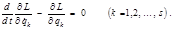 (2.5.9)
(2.5.9) уравнения движения (2.5.9) также инвариантны по отношению к этим преобразованиям.
уравнения движения (2.5.9) также инвариантны по отношению к этим преобразованиям.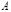 и
и  , каждая из которых, будучи замкнутой, имела бы функции Лагранжа
, каждая из которых, будучи замкнутой, имела бы функции Лагранжа 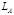 и
и 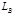 соответственно. Тогда при разведении частей так далеко, что взаимодействием между ними можно пренебречь, лагранжиан системы в целом стремится к пределу
соответственно. Тогда при разведении частей так далеко, что взаимодействием между ними можно пренебречь, лагранжиан системы в целом стремится к пределу  (2.5.10)
(2.5.10)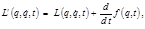 (2.5.11), то
(2.5.11), то (2.5.12)
(2.5.12) , и если
, и если  , то и
, то и  . Вид уравнений движения остается неизменным.
. Вид уравнений движения остается неизменным.


