Задача двух тел. Движение в центральном поле
Похожие статьи вашей тематики
Полное решение в общем виде допускает чрезвычайно важная задача о движении замкнутой системы из двух взаимодействующих частиц (задача двух тел). Решение этой задачи используется в небесной механике, при изучении столкновений частиц, в статистической физике и т. д. Задача двух тел существенно упрощается при разложении движения системы на движение ее центра инерции и движение частиц относительно центра инерции.
Итак, рассмотрим консервативную систему двух частиц. Потенциальная энергия их взаимодействия зависит от расстояния между частицами (и, естественно, от масс, зарядов и т. д.). Введем вектор относительно расстояния (радиус-вектор первой частицы относительно второй):
 (4.2.1) (4.2.1)
Тогда потенциальная энергия  и функция Лагранжа и функция Лагранжа
 (4.2.2) (4.2.2)
В системе центра инерции  (4.2.3) (4.2.3)
что совместно с (4.2.1) дает:
 (4.2.4) и (4.2.4) и
 (4.2.5) (4.2.5)
где  – приведенная масса: – приведенная масса: 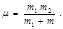 (4.2.6) (4.2.6)
(4.2.5) формально совпадает с функцией Лагранжа для одной частицы массой  , движущейся в поле , движущейся в поле  . По решению . По решению  этой задачи уравнения этой задачи уравнения  и и  для каждой из частиц с массами для каждой из частиц с массами  и и  в отдельности (в системе их общего центра инерции) получаются по формулам (4.2.4). в отдельности (в системе их общего центра инерции) получаются по формулам (4.2.4).
Таким образом, уравнение (4.2.5) описывает движение изображающей точки массой  в поле в поле  , зависящем от расстояния , зависящем от расстояния  этой точки до центра инерции рассматриваемой системы тел; этой точки до центра инерции рассматриваемой системы тел; 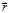 – радиус-вектор этой изображающей точки. Векторы – радиус-вектор этой изображающей точки. Векторы  и и 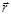 всегда в одной плоскости. Из (4.2.4) следует, что траектории частиц системы и изображающей точки – подобные относительно центра инерции кривые (см. подробнее [4, с. 145]). всегда в одной плоскости. Из (4.2.4) следует, что траектории частиц системы и изображающей точки – подобные относительно центра инерции кривые (см. подробнее [4, с. 145]).
Поскольку начало координат связано с центром инерции,  – радиус-вектор изображающей точки относительно центра инерции, то и действующая на эту точку сила – радиус-вектор изображающей точки относительно центра инерции, то и действующая на эту точку сила
 (4.2.7) (4.2.7)
центральная, причем равная по модулю силе взаимодействия между частицами системы (других сил здесь нет). По третьему закону Ньютона
 (4.2.8) (4.2.8)
Итак, задача о движении двух тел сводится к задаче о движении одной частицы в центральном поле, в котором потенциальная энергия этой частицы зависит только от расстояния  до определенной неподвижной точки (полюса). Сила, действующая на такую частицу, по модулю зависит только от до определенной неподвижной точки (полюса). Сила, действующая на такую частицу, по модулю зависит только от  и направлена в каждой точке вдоль радиус-вектора. и направлена в каждой точке вдоль радиус-вектора.
Момент центральной силы относительно полюса равен нулю, поэтому момент импульса  рассматриваемой частицы сохраняется. Из сохранения направления вектора рассматриваемой частицы сохраняется. Из сохранения направления вектора  следует, что движение частицы происходит в одной плоскости, т. е. ее траектория – плоская кривая. Далее сохраним обычное обозначение следует, что движение частицы происходит в одной плоскости, т. е. ее траектория – плоская кривая. Далее сохраним обычное обозначение  массы рассматриваемой частицы. Для плоского движения целесообразно применять полярные координаты массы рассматриваемой частицы. Для плоского движения целесообразно применять полярные координаты  . Тогда функция Лагранжа запишется в виде: . Тогда функция Лагранжа запишется в виде:
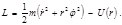 (4.2.9) (4.2.9)
Лагранжиан не зависит явно от координаты  , т. е. эта координата циклическая. Для такой координаты , т. е. эта координата циклическая. Для такой координаты
 (4.2.10) (4.2.10)
т. е. соответствующий ей обобщенный импульс  является интегралом движения, что существенно упрощает задачу интегрирования уравнений движения. В нашем случае обобщенный импульс является интегралом движения, что существенно упрощает задачу интегрирования уравнений движения. В нашем случае обобщенный импульс  совпадает с моментом импульса, и мы возвращаемся к уже упомянутому закону сохранения совпадает с моментом импульса, и мы возвращаемся к уже упомянутому закону сохранения
 (4.2.11) (4.2.11)
Для плоского движения одной частицы в центральном поле закон сохранения момента импульса допускает простую геометрическую интерпретацию. Выражение  представляет собой площадь сектора, образованного двумя бесконечно близкими радиус-векторами и элементом дуги траектории. Обозначив ее как представляет собой площадь сектора, образованного двумя бесконечно близкими радиус-векторами и элементом дуги траектории. Обозначив ее как  , запишем выражение для момента импульса частицы в виде , запишем выражение для момента импульса частицы в виде
 (4.2.12) (4.2.12)
где  – секториальная скорость. Сохранение момента импульса означает постоянство секториальной скорости: за любые равные промежутки времени радиус-вектор частицы описывает равные площади (закон площадей Кеплера). Закон сохранения момента импульса частицы в центральном поле связан, таким образом, с так называемым интегралом площадей. – секториальная скорость. Сохранение момента импульса означает постоянство секториальной скорости: за любые равные промежутки времени радиус-вектор частицы описывает равные площади (закон площадей Кеплера). Закон сохранения момента импульса частицы в центральном поле связан, таким образом, с так называемым интегралом площадей.
Имеется еще один интеграл движения – в поле консервативных сил сохраняется механическая энергия частицы:
 (4.2.13) (4.2.13)
Подставляя (4.2.11) в (4.2.13), находим:
 (4.2.14) (4.2.14)
Отсюда
 (4.2.15) (4.2.15)
Разделяя переменные и интегрируя, получим:
 (4.2.16) (4.2.16)
Вычислив интеграл (4.2.16), можно получить первое уравнение движения  (к сожалению, далеко не всегда в явном виде). Используя далее (4.2.11), имеем: (к сожалению, далеко не всегда в явном виде). Используя далее (4.2.11), имеем:  (4.2.17) (4.2.17)
 (4.2.18) (4.2.18)
что дает (при условии возможности взять интеграл) уравнение траектории  , а из (4.2.17) при известном , а из (4.2.17) при известном  получаем второе уравнение движения получаем второе уравнение движения  . .
Итак, в зависимости от вида 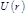 задача решается (аналитически или численно). Заметим, что угол задача решается (аналитически или численно). Заметим, что угол  всегда изменяется со временем монотонно (из (4.2.11) видно, что всегда изменяется со временем монотонно (из (4.2.11) видно, что  никогда не меняет знак). никогда не меняет знак).
(4.2.14) показывает, что радиальную часть движения можно рассматривать как одномерное движение в поле с «эффективной» потенциальной энергией
 (4.2.19) (4.2.19)
Второе слагаемое в (4.2.19) иногда называют центробежной энергией. Вполне понятно, что  . .
Значения  , при которых , при которых  , определяют границы области движения по расстоянию от центра. При выполнении этого равенства радиальная скорость , определяют границы области движения по расстоянию от центра. При выполнении этого равенства радиальная скорость  обращается в нуль, что не означает остановки частицы (как при истинно одномерном движении), поскольку угловая скорость обращается в нуль, что не означает остановки частицы (как при истинно одномерном движении), поскольку угловая скорость  не обращается в нуль при этом. Равенство не обращается в нуль при этом. Равенство  соответствует «точке поворота» траектории, в которой функция соответствует «точке поворота» траектории, в которой функция  переходит от увеличения к уменьшению или наоборот. Если область движения имеет одну границу переходит от увеличения к уменьшению или наоборот. Если область движения имеет одну границу  – движение инфинитное, если две границы – движение инфинитное, если две границы  – движение финитное (траектория целиком лежит внутри кольца, ограниченного радиусами – движение финитное (траектория целиком лежит внутри кольца, ограниченного радиусами 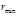 и и  ). За время, в течение которого ). За время, в течение которого  изменяется от изменяется от  до до  и снова до и снова до  , радиус-вектор частицы повернется на угол (см. (4.2.18)) , радиус-вектор частицы повернется на угол (см. (4.2.18))
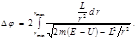 (4.2.20) (4.2.20)
Условие замкнутости траектории заключается в том, что угол  равен рациональной части от равен рациональной части от  , т. е. , т. е.
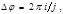 (4.2.21) (4.2.21)
где  и и  – целые числа. Тогда, сделав – целые числа. Тогда, сделав  полных оборотов и повторив эту операцию полных оборотов и повторив эту операцию  раз, радиус-вектор частицы совпадает с первоначальным значением, и траектория замкнется. Существуют только два типа центральных полей, в которых все траектории финитных движений замкнуты: раз, радиус-вектор частицы совпадает с первоначальным значением, и траектория замкнется. Существуют только два типа центральных полей, в которых все траектории финитных движений замкнуты:  и и 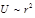 . Первый будет рассмотрен в следующем подразделе (задача Кеплера). . Первый будет рассмотрен в следующем подразделе (задача Кеплера).
При движении с 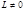 наличие центробежной энергии, обращающейся в бесконечность при наличие центробежной энергии, обращающейся в бесконечность при  , обычно приводит к невозможности проникновения частицы к центру поля, даже если последнее имеет характер притяжения. «Падение» в центр возможно, если потенциальная энергия достаточно быстро стремится к , обычно приводит к невозможности проникновения частицы к центру поля, даже если последнее имеет характер притяжения. «Падение» в центр возможно, если потенциальная энергия достаточно быстро стремится к  при при  . Поскольку . Поскольку
 (4.2.22) или (4.2.22) или
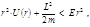 (4.2.23) (4.2.23)
то  может принимать сколь угодно малые значения лишь при условии может принимать сколь угодно малые значения лишь при условии
 (4.2.24) (4.2.24)
т. е. функция  должна стремиться к должна стремиться к  либо как либо как  с с  , либо пропорционально , либо пропорционально 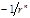 , где , где  . .
Рассмотрим этот вопрос на качественном уровне. В большинстве случаев  , где , где  (определяется характеристиками поля и частицы); (определяется характеристиками поля и частицы);  для поля притяжения и для поля притяжения и  для поля отталкивания. Пусть для поля отталкивания. Пусть  . Рассмотрим частные случаи: . Рассмотрим частные случаи:
1)  (слабо сингулярное поле притяжения). (слабо сингулярное поле притяжения).
 (4.2.25) (4.2.25)
Легко видеть, что при отрицательных значениях энергии Е движение происходит в области 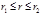 (при (при  частица движется по окружности с радиусом частица движется по окружности с радиусом  ) по траекториям эллиптического типа; при ) по траекториям эллиптического типа; при 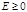 траектории параболического или гиперболического типа, т. е. частица не может попасть на силовой центр ( траектории параболического или гиперболического типа, т. е. частица не может попасть на силовой центр ( ), но может удалиться от силового центра на бесконечно большое расстояние. При ), но может удалиться от силового центра на бесконечно большое расстояние. При  траектория незамкнутая, например, траектория Меркурия, для которого наблюдается заметное смещение перигелия. траектория незамкнутая, например, траектория Меркурия, для которого наблюдается заметное смещение перигелия.
 Если при Если при   , то , то  . Тогда при любых начальных условиях движение частицы чисто радиальное (одномерное), причем при любых . Тогда при любых начальных условиях движение частицы чисто радиальное (одномерное), причем при любых  возможен захват частицы силовым центром (рисунок 4.2.2), если возможен захват частицы силовым центром (рисунок 4.2.2), если  . При . При  и и  происходит уход частицы на бесконечность. При происходит уход частицы на бесконечность. При  и и 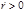 частица уходит от центра, а затем при частица уходит от центра, а затем при  поворачивает и начинает падение на центр. поворачивает и начинает падение на центр.
Рисунок 4.2.2
Чисто эллиптические (параболические, гиперболические) траектории имеют место при  , т. е. , т. е.  . Это утверждение носит наименование теорема Бертрана (часть теоремы, т. к. эллиптические траектории имеют место и при . Это утверждение носит наименование теорема Бертрана (часть теоремы, т. к. эллиптические траектории имеют место и при  ). ).
2)   (4.2.26) (4.2.26)
В этом случае имеет место ситуация, очевидная из рисунка 4.2.3.
Рисунок 4.2.3
3)  (сильно сингулярное поле притяжения) (сильно сингулярное поле притяжения)
 (4.2.27) (4.2.27)
Этот случай иллюстрирует рисунок 4.2.4.
Рисунок 4.2.4
Задача Кеплера
Частный случай задачи о движении частицы в центральном поле – задача о движении в поле притяжения кулоновского типа (например, задача о движении в поле тяготения). В этом случае  , где , где  . Найдем траекторию частицы массой . Найдем траекторию частицы массой 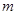 в таком поле в дифференциальной и интегральной формах. в таком поле в дифференциальной и интегральной формах.
Известно, что в рассматриваемом случае
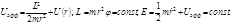 (4.3.1) (4.3.1)
Тогда функцию Лагранжа 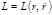 можно представить в виде: можно представить в виде:  (4.3.2) (4.3.2)
т. е. рассматривается движение частицы с обобщенной координатой  и обобщенной скоростью и обобщенной скоростью 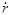 в поле с потенциалом в поле с потенциалом 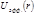 . Подставляя (4.3.2) в уравнение Лагранжа, получаем: . Подставляя (4.3.2) в уравнение Лагранжа, получаем:
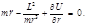 (4.3.3) (4.3.3)
Заметим, что (4.3.3) можно получить и непосредственным дифференцированием механической энергии  по времени (учитывая, что по времени (учитывая, что 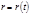 ). Учтем далее, что ). Учтем далее, что  и и 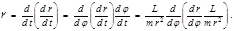 (4.3.4) (4.3.4)
Тогда из (4.3.3) находим:
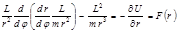 (4.3.5) или (4.3.5) или
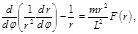 (4.3.6) (4.3.6)
где 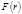 – проекция силы – проекция силы  на направление на направление 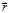 . Обозначим . Обозначим 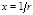 . При этом . При этом 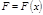 и и
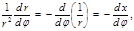 (4.3.7) (4.3.7) 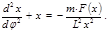 (4.3.8) (4.3.8)
Это формула Бине – дифференциальной уравнение траектории при заданной силе. Если  , то , то
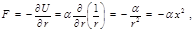 (4.3.9) (4.3.9)
знак 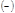 показывает, что это сила притяжения. Дифференциальное уравнение траектории в поле притяжения кулоновского типа: показывает, что это сила притяжения. Дифференциальное уравнение траектории в поле притяжения кулоновского типа:
 (4.3.10) (4.3.10)
Постоянная 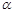 зависит от масс (зарядов) тел и выбора системы единиц. зависит от масс (зарядов) тел и выбора системы единиц.
Учитывая, что
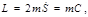 (4.3.11) (4.3.11)
где 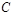 – удвоенная секториальная скорость, для любого поля притяжения кулоновского типа имеем: – удвоенная секториальная скорость, для любого поля притяжения кулоновского типа имеем:
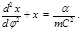 (4.3.12) (4.3.12)
В частности, для поля тяготения
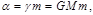 (4.3.13) (4.3.13)
где 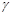 – гауссова постоянная, – гауссова постоянная,  – постоянная тяготения, – постоянная тяготения, 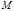 – масса тела, в поле тяготения которого движется частица массой – масса тела, в поле тяготения которого движется частица массой 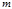 (тело (тело 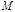 неподвижно). неподвижно).
Для описания движения двух тел с массами 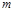 и и 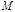 в системе их центра инерции используют понятие изображающей точки с массой в системе их центра инерции используют понятие изображающей точки с массой 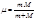 , расстояние которой от центра инерции , расстояние которой от центра инерции 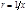 . Уравнение траектории этой точки . Уравнение траектории этой точки  (4.3.14) или (4.3.14) или 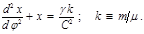 (4.3.15) (4.3.15)
Это неоднородное дифференциальное уравнение второго порядка, общее решение которого
 (4.3.16) (4.3.16)
где 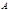 и и 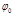 – произвольные постоянные, – произвольные постоянные, 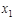 – общее решение соответствующего (4.3.15) однородного уравнения, – общее решение соответствующего (4.3.15) однородного уравнения, 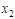 – частное решение (4.3.15). Тогда – частное решение (4.3.15). Тогда 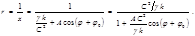 (4.3.17) (4.3.17)
В полярных координатах уравнение конического сечения
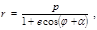 (4.3.18) (4.3.18)
где 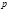 – параметр кривой, – параметр кривой,  – эксцентриситет. Итак, в поле тяготения (в поле притяжения кулоновского типа) частица (или изображающая точка для замкнутой системы двух частиц) движется по траектории, представляющей собой одно из конических сечений. В нашем случае – эксцентриситет. Итак, в поле тяготения (в поле притяжения кулоновского типа) частица (или изображающая точка для замкнутой системы двух частиц) движется по траектории, представляющей собой одно из конических сечений. В нашем случае
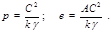 (4.3.19) (4.3.19)
Вид траектории определяют константы  и и 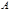 , причем , причем  , а полная энергия , а полная энергия  определяет величину определяет величину  . .
Заметим, что интегральное уравнение траектории можно легко получить из (4.3.18), подставляя  и интегрируя: и интегрируя:
 (4.3.20) (4.3.20)
Если  , то , то
 (4.3.21) (4.3.21)
что при  , ,  , ,  совпадает с (4.3.17); при этом совпадает с (4.3.17); при этом
 (4.3.22) (4.3.22)
 (4.3.23) (4.3.23)
Постоянная 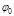 задает положение траектории на плоскости; при задает положение траектории на плоскости; при  точка с точка с 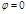 – ближайшая к полюсу (перигелий орбиты). – ближайшая к полюсу (перигелий орбиты).
При 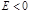 эксцентриситет эксцентриситет  , траектория – эллипс; если его полуоси , траектория – эллипс; если его полуоси  и и  , то параметр , то параметр  , площадь , площадь  , секториальная скорость , секториальная скорость  , где , где  – период (время одного полного оборота частицы). Точки – период (время одного полного оборота частицы). Точки  и и 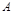 – соответственно перигелий и афелий (для спутника Земли – перигей и апогей). – соответственно перигелий и афелий (для спутника Земли – перигей и апогей).
Используя известные формулы аналитической геометрии, выразим полуоси эллипса:
 (4.3.24) (4.3.24)
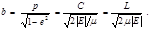 (4.3.25) (4.3.25)
Наименьшее и наибольшее расстояния от центра поля (фокуса эллипса):
 (4.3.26) (4.3.26)
Зная  , вычислить , вычислить  и и 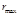 можно легко (эти величины могут быть найдены также как корни уравнения можно легко (эти величины могут быть найдены также как корни уравнения  ). Период движения изображающей точки по эллипсу определяется энергией: ). Период движения изображающей точки по эллипсу определяется энергией:
 (4.3.27) (4.3.27)
В частном случае движения по окружности  . .
При  движение инфинитное ( движение инфинитное ( – парабола, – парабола,  – гипербола). Гиперболической траектории соответствует энергия – гипербола). Гиперболической траектории соответствует энергия  . При этом расстояние перигелия от центра поля . При этом расстояние перигелия от центра поля
 , (4.3.28) , (4.3.28)
где «полуось» орбиты  . (4.3.29) . (4.3.29)
Для параболической траектории  , ,  и и
 (4.3.30) (4.3.30)
Последний случай может осуществляться, если частица (изображающая точка) начинает движение из состояния покоя на бесконечности.
Вычислим теперь скорость движения изображающей точки в разных местах траектории (конического сечения). В полярных координатах
 . (4.3.31) . (4.3.31)
Учитывая, что  , ,  , находим: , находим:
 . (4.3.32) . (4.3.32)
Используя уравнение 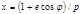 для для  , получаем: , получаем:
 . (4.3.33) . (4.3.33)
Для эллипса  . Исследуя на экстремум выражение . Исследуя на экстремум выражение
 , (4.3.34) , (4.3.34)
находим:
 при при  , (4.3.35) , (4.3.35)
 при при  . (4.3.35) . (4.3.35)
Для параболы  , ,
 , (4.3.36) , (4.3.36)
 при при  , (4.3.37) , (4.3.37)
 при при  . (4.3.38) . (4.3.38)
Для гиперболы  , при этом и в случае , при этом и в случае   . .
|



 (4.2.1)
(4.2.1) и функция Лагранжа
и функция Лагранжа (4.2.2)
(4.2.2) (4.2.3)
(4.2.3) (4.2.4) и
(4.2.4) и (4.2.5)
(4.2.5) – приведенная масса:
– приведенная масса: 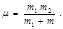 (4.2.6)
(4.2.6) , движущейся в поле
, движущейся в поле  . По решению
. По решению  этой задачи уравнения
этой задачи уравнения  и
и  для каждой из частиц с массами
для каждой из частиц с массами  и
и  в отдельности (в системе их общего центра инерции) получаются по формулам (4.2.4).
в отдельности (в системе их общего центра инерции) получаются по формулам (4.2.4). в поле
в поле  , зависящем от расстояния
, зависящем от расстояния  этой точки до центра инерции рассматриваемой системы тел;
этой точки до центра инерции рассматриваемой системы тел; 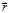 – радиус-вектор этой изображающей точки. Векторы
– радиус-вектор этой изображающей точки. Векторы  и
и 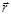 всегда в одной плоскости. Из (4.2.4) следует, что траектории частиц системы и изображающей точки – подобные относительно центра инерции кривые (см. подробнее [4, с. 145]).
всегда в одной плоскости. Из (4.2.4) следует, что траектории частиц системы и изображающей точки – подобные относительно центра инерции кривые (см. подробнее [4, с. 145]). – радиус-вектор изображающей точки относительно центра инерции, то и действующая на эту точку сила
– радиус-вектор изображающей точки относительно центра инерции, то и действующая на эту точку сила (4.2.7)
(4.2.7) (4.2.8)
(4.2.8) до определенной неподвижной точки (полюса). Сила, действующая на такую частицу, по модулю зависит только от
до определенной неподвижной точки (полюса). Сила, действующая на такую частицу, по модулю зависит только от  и направлена в каждой точке вдоль радиус-вектора.
и направлена в каждой точке вдоль радиус-вектора. рассматриваемой частицы сохраняется. Из сохранения направления вектора
рассматриваемой частицы сохраняется. Из сохранения направления вектора  следует, что движение частицы происходит в одной плоскости, т. е. ее траектория – плоская кривая. Далее сохраним обычное обозначение
следует, что движение частицы происходит в одной плоскости, т. е. ее траектория – плоская кривая. Далее сохраним обычное обозначение  массы рассматриваемой частицы. Для плоского движения целесообразно применять полярные координаты
массы рассматриваемой частицы. Для плоского движения целесообразно применять полярные координаты  . Тогда функция Лагранжа запишется в виде:
. Тогда функция Лагранжа запишется в виде: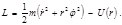 (4.2.9)
(4.2.9) , т. е. эта координата циклическая. Для такой координаты
, т. е. эта координата циклическая. Для такой координаты (4.2.10)
(4.2.10) является интегралом движения, что существенно упрощает задачу интегрирования уравнений движения. В нашем случае обобщенный импульс
является интегралом движения, что существенно упрощает задачу интегрирования уравнений движения. В нашем случае обобщенный импульс  совпадает с моментом импульса, и мы возвращаемся к уже упомянутому закону сохранения
совпадает с моментом импульса, и мы возвращаемся к уже упомянутому закону сохранения (4.2.11)
(4.2.11) представляет собой площадь сектора, образованного двумя бесконечно близкими радиус-векторами и элементом дуги траектории. Обозначив ее как
представляет собой площадь сектора, образованного двумя бесконечно близкими радиус-векторами и элементом дуги траектории. Обозначив ее как  , запишем выражение для момента импульса частицы в виде
, запишем выражение для момента импульса частицы в виде (4.2.12)
(4.2.12) – секториальная скорость. Сохранение момента импульса означает постоянство секториальной скорости: за любые равные промежутки времени радиус-вектор частицы описывает равные площади (закон площадей Кеплера). Закон сохранения момента импульса частицы в центральном поле связан, таким образом, с так называемым интегралом площадей.
– секториальная скорость. Сохранение момента импульса означает постоянство секториальной скорости: за любые равные промежутки времени радиус-вектор частицы описывает равные площади (закон площадей Кеплера). Закон сохранения момента импульса частицы в центральном поле связан, таким образом, с так называемым интегралом площадей. (4.2.13)
(4.2.13) (4.2.14)
(4.2.14) (4.2.15)
(4.2.15) (4.2.16)
(4.2.16) (к сожалению, далеко не всегда в явном виде). Используя далее (4.2.11), имеем:
(к сожалению, далеко не всегда в явном виде). Используя далее (4.2.11), имеем:  (4.2.17)
(4.2.17) (4.2.18)
(4.2.18) , а из (4.2.17) при известном
, а из (4.2.17) при известном  получаем второе уравнение движения
получаем второе уравнение движения  .
.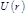 задача решается (аналитически или численно). Заметим, что угол
задача решается (аналитически или численно). Заметим, что угол  всегда изменяется со временем монотонно (из (4.2.11) видно, что
всегда изменяется со временем монотонно (из (4.2.11) видно, что  никогда не меняет знак).
никогда не меняет знак). (4.2.19)
(4.2.19) .
. , определяют границы области движения по расстоянию от центра. При выполнении этого равенства радиальная скорость
, определяют границы области движения по расстоянию от центра. При выполнении этого равенства радиальная скорость  обращается в нуль, что не означает остановки частицы (как при истинно одномерном движении), поскольку угловая скорость
обращается в нуль, что не означает остановки частицы (как при истинно одномерном движении), поскольку угловая скорость  не обращается в нуль при этом. Равенство
не обращается в нуль при этом. Равенство  соответствует «точке поворота» траектории, в которой функция
соответствует «точке поворота» траектории, в которой функция  переходит от увеличения к уменьшению или наоборот. Если область движения имеет одну границу
переходит от увеличения к уменьшению или наоборот. Если область движения имеет одну границу  – движение инфинитное, если две границы
– движение инфинитное, если две границы  – движение финитное (траектория целиком лежит внутри кольца, ограниченного радиусами
– движение финитное (траектория целиком лежит внутри кольца, ограниченного радиусами 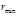 и
и  ). За время, в течение которого
). За время, в течение которого  изменяется от
изменяется от  до
до  и снова до
и снова до  , радиус-вектор частицы повернется на угол (см. (4.2.18))
, радиус-вектор частицы повернется на угол (см. (4.2.18))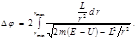 (4.2.20)
(4.2.20) равен рациональной части от
равен рациональной части от  , т. е.
, т. е.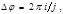 (4.2.21)
(4.2.21) и
и  – целые числа. Тогда, сделав
– целые числа. Тогда, сделав  и
и 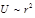 . Первый будет рассмотрен в следующем подразделе (задача Кеплера).
. Первый будет рассмотрен в следующем подразделе (задача Кеплера).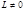 наличие центробежной энергии, обращающейся в бесконечность при
наличие центробежной энергии, обращающейся в бесконечность при  , обычно приводит к невозможности проникновения частицы к центру поля, даже если последнее имеет характер притяжения. «Падение» в центр возможно, если потенциальная энергия достаточно быстро стремится к
, обычно приводит к невозможности проникновения частицы к центру поля, даже если последнее имеет характер притяжения. «Падение» в центр возможно, если потенциальная энергия достаточно быстро стремится к  при
при  . Поскольку
. Поскольку (4.2.22) или
(4.2.22) или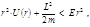 (4.2.23)
(4.2.23) может принимать сколь угодно малые значения лишь при условии
может принимать сколь угодно малые значения лишь при условии (4.2.24)
(4.2.24) должна стремиться к
должна стремиться к  либо как
либо как  с
с  , либо пропорционально
, либо пропорционально 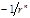 , где
, где  .
. , где
, где  (определяется характеристиками поля и частицы);
(определяется характеристиками поля и частицы);  для поля притяжения и
для поля притяжения и  для поля отталкивания. Пусть
для поля отталкивания. Пусть  . Рассмотрим частные случаи:
. Рассмотрим частные случаи: (слабо сингулярное поле притяжения).
(слабо сингулярное поле притяжения). (4.2.25)
(4.2.25)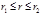 (при
(при  частица движется по окружности с радиусом
частица движется по окружности с радиусом  ) по траекториям эллиптического типа; при
) по траекториям эллиптического типа; при 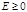 траектории параболического или гиперболического типа, т. е. частица не может попасть на силовой центр (
траектории параболического или гиперболического типа, т. е. частица не может попасть на силовой центр ( ), но может удалиться от силового центра на бесконечно большое расстояние. При
), но может удалиться от силового центра на бесконечно большое расстояние. При  траектория незамкнутая, например, траектория Меркурия, для которого наблюдается заметное смещение перигелия.
траектория незамкнутая, например, траектория Меркурия, для которого наблюдается заметное смещение перигелия. Если при
Если при 
 , то
, то  . Тогда при любых начальных условиях движение частицы чисто радиальное (одномерное), причем при любых
. Тогда при любых начальных условиях движение частицы чисто радиальное (одномерное), причем при любых  возможен захват частицы силовым центром (рисунок 4.2.2), если
возможен захват частицы силовым центром (рисунок 4.2.2), если  . При
. При  и
и  происходит уход частицы на бесконечность. При
происходит уход частицы на бесконечность. При  и
и 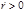 частица уходит от центра, а затем при
частица уходит от центра, а затем при  поворачивает и начинает падение на центр.
поворачивает и начинает падение на центр.
 , т. е.
, т. е.  . Это утверждение носит наименование теорема Бертрана (часть теоремы, т. к. эллиптические траектории имеют место и при
. Это утверждение носит наименование теорема Бертрана (часть теоремы, т. к. эллиптические траектории имеют место и при  ).
).
 (4.2.26)
(4.2.26)
 (сильно сингулярное поле притяжения)
(сильно сингулярное поле притяжения) (4.2.27)
(4.2.27)
 , где
, где  . Найдем траекторию частицы массой
. Найдем траекторию частицы массой 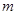 в таком поле в дифференциальной и интегральной формах.
в таком поле в дифференциальной и интегральной формах.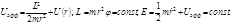 (4.3.1)
(4.3.1)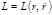 можно представить в виде:
можно представить в виде:  (4.3.2)
(4.3.2)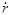 в поле с потенциалом
в поле с потенциалом 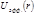 . Подставляя (4.3.2) в уравнение Лагранжа, получаем:
. Подставляя (4.3.2) в уравнение Лагранжа, получаем: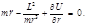 (4.3.3)
(4.3.3) по времени (учитывая, что
по времени (учитывая, что 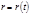 ). Учтем далее, что
). Учтем далее, что  и
и 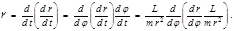 (4.3.4)
(4.3.4)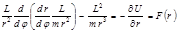 (4.3.5) или
(4.3.5) или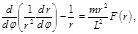 (4.3.6)
(4.3.6)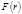 – проекция силы
– проекция силы  на направление
на направление 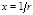 . При этом
. При этом 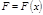 и
и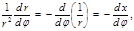 (4.3.7)
(4.3.7) 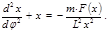 (4.3.8)
(4.3.8) , то
, то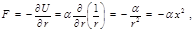 (4.3.9)
(4.3.9)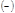 показывает, что это сила притяжения. Дифференциальное уравнение траектории в поле притяжения кулоновского типа:
показывает, что это сила притяжения. Дифференциальное уравнение траектории в поле притяжения кулоновского типа: (4.3.10)
(4.3.10)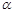 зависит от масс (зарядов) тел и выбора системы единиц.
зависит от масс (зарядов) тел и выбора системы единиц.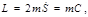 (4.3.11)
(4.3.11)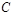 – удвоенная секториальная скорость, для любого поля притяжения кулоновского типа имеем:
– удвоенная секториальная скорость, для любого поля притяжения кулоновского типа имеем: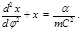 (4.3.12)
(4.3.12)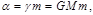 (4.3.13)
(4.3.13)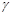 – гауссова постоянная,
– гауссова постоянная,  – постоянная тяготения,
– постоянная тяготения, 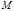 – масса тела, в поле тяготения которого движется частица массой
– масса тела, в поле тяготения которого движется частица массой 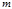 (тело
(тело 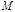 неподвижно).
неподвижно).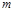 и
и 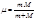 , расстояние которой от центра инерции
, расстояние которой от центра инерции 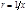 . Уравнение траектории этой точки
. Уравнение траектории этой точки  (4.3.14) или
(4.3.14) или 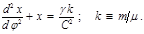 (4.3.15)
(4.3.15) (4.3.16)
(4.3.16)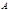 и
и 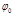 – произвольные постоянные,
– произвольные постоянные, 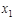 – общее решение соответствующего (4.3.15) однородного уравнения,
– общее решение соответствующего (4.3.15) однородного уравнения, 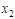 – частное решение (4.3.15). Тогда
– частное решение (4.3.15). Тогда 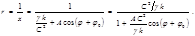 (4.3.17)
(4.3.17)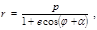 (4.3.18)
(4.3.18)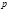 – параметр кривой,
– параметр кривой,  – эксцентриситет. Итак, в поле тяготения (в поле притяжения кулоновского типа) частица (или изображающая точка для замкнутой системы двух частиц) движется по траектории, представляющей собой одно из конических сечений. В нашем случае
– эксцентриситет. Итак, в поле тяготения (в поле притяжения кулоновского типа) частица (или изображающая точка для замкнутой системы двух частиц) движется по траектории, представляющей собой одно из конических сечений. В нашем случае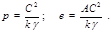 (4.3.19)
(4.3.19) и
и 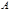 , причем
, причем  , а полная энергия
, а полная энергия  определяет величину
определяет величину  .
. и интегрируя:
и интегрируя: (4.3.20)
(4.3.20) , то
, то (4.3.21)
(4.3.21) ,
,  ,
,  совпадает с (4.3.17); при этом
совпадает с (4.3.17); при этом (4.3.22)
(4.3.22) (4.3.23)
(4.3.23)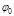 задает положение траектории на плоскости; при
задает положение траектории на плоскости; при  точка с
точка с 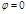 – ближайшая к полюсу (перигелий орбиты).
– ближайшая к полюсу (перигелий орбиты).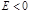 эксцентриситет
эксцентриситет  , траектория – эллипс; если его полуоси
, траектория – эллипс; если его полуоси  и
и  , то параметр
, то параметр  , площадь
, площадь  , секториальная скорость
, секториальная скорость  , где
, где  – период (время одного полного оборота частицы). Точки
– период (время одного полного оборота частицы). Точки  и
и 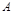 – соответственно перигелий и афелий (для спутника Земли – перигей и апогей).
– соответственно перигелий и афелий (для спутника Земли – перигей и апогей). (4.3.24)
(4.3.24)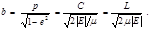 (4.3.25)
(4.3.25) (4.3.26)
(4.3.26) , вычислить
, вычислить 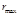 можно легко (эти величины могут быть найдены также как корни уравнения
можно легко (эти величины могут быть найдены также как корни уравнения  ). Период движения изображающей точки по эллипсу определяется энергией:
). Период движения изображающей точки по эллипсу определяется энергией: (4.3.27)
(4.3.27) .
. движение инфинитное (
движение инфинитное ( – парабола,
– парабола,  – гипербола). Гиперболической траектории соответствует энергия
– гипербола). Гиперболической траектории соответствует энергия  . При этом расстояние перигелия от центра поля
. При этом расстояние перигелия от центра поля , (4.3.28)
, (4.3.28) . (4.3.29)
. (4.3.29) ,
,  и
и (4.3.30)
(4.3.30) . (4.3.31)
. (4.3.31) ,
,  , находим:
, находим: . (4.3.32)
. (4.3.32)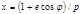 для
для  , получаем:
, получаем: . (4.3.33)
. (4.3.33) . Исследуя на экстремум выражение
. Исследуя на экстремум выражение , (4.3.34)
, (4.3.34) при
при  , (4.3.35)
, (4.3.35) при
при  . (4.3.35)
. (4.3.35) ,
, , (4.3.36)
, (4.3.36) при
при  , (4.3.37)
, (4.3.37) при
при  . (4.3.38)
. (4.3.38) , при этом и в случае
, при этом и в случае 
 .
.


