
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложное движение точки. Теорема о сложении скоростей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сложным называется такое движение точки, при котором она одновременно участвует в нескольких движениях. Абсолютным движением называется движение точки по отношению к неподвижной системе отсчета. Относительным называется движение точки по отношению к подвижной системе отсчета. Переносным называется движение той точки подвижной системы отсчета, в которой находится движущаяся точка, по отношению к неподвижной. Проще можно сказать: относительным движением называется движение точки по телу, а переносным движением - движение точки вместе с телом. Скорость и ускорение точки по отношению к неподвижной системе отсчета называются абсолютными (v, а). Скорость и ускорение точки по отношению к подвижной системе отсчета называются относительными (v Теорема: скорость точки в абсолютном движении геометрически складывается из переносной и относительной скорости.
20. Теорема о сложении ускорений при сложном движении. Теорема: абсолютное ускорение точки геометрически складывается из переносного, относительного и Кориолисова ускорений.
где:
Ускорение Кориолиса равно нулю если: 1. 2. 3. Задача К1 По заданным уравнениям движения точки в плоскости xy: Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки. В данной задаче все искомые величины нужно определить только для момента времени t1 = π/6 c. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует применить известные из тригонометрии формулы:
При выборе масштабов построения траектории, скоростей и ускорений следует учитывать, что они должны быть стандартными, то есть из ряда: 1, 2, 25, 4, 5. При этом изображаемые вектора должны быть достаточно крупными (50 - 100 мм). Таблица К1
Пример К1. Даны уравнения движения точки в плоскости xy:
Определить уравнение траектории точки; для момента времени t1=1c найти скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории. Решение. 1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу.
следовательно: Отсюда окончательно находим следующее уравнение траектории точки (рис. К1): 2. Скорость точки найдем по ее проекциям на координатные оси:
и при t = 1c: 3. Аналогично найдем ускорение точки:
и при t = 1c: 4. Касательное ускорение найдем, дифференцируя по времени равенство: Подставив полученные ранее значения, найдем, что при t = 1c: aτ = 0,66 см/с2. 5. Нормальное ускорение точки: 6. Радиус кривизны траектории: При построении скоростей следует в данном случае выбрать масштаб: μ v = 0,02 l vx = │vx │ / μ v = 1,11/0,02 ≈ 56 мм, l vy = │vy │ / μ v = 0,73/0,02 ≈ 37 мм; или μ v = 0,01 l vx = │vx │ / μ v = 1,11/0,01 = 111 мм, l vy = │vy │ / μ v = 0,73/0,01 = 73 мм. При построении ускорений следует выбрать масштаб: μ a = 0,01 l ax = │ a x │ / μ a = 0,87/0,01 = 87 мм, l ay = │ a y │ / μ a = 0,12/0,01 = 12 мм; l aτ = │ aτ │ / μ a = 0,66/0,01 = 66 мм, l an = │ an │ / μ a = 0,58/0,01 = 58 мм. Найденные длины отрезков откладываем из точки с координатами: при t = 1c: Замечание: при построении следует учесть, что l ay необходимо отложить вниз, так как: ay < 0, а aτ – по направлению скорости, так как aτ > 0. Задача К2 Механизм состоит из ступенчатых колес 2-3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 1, привязанного к концу нити, намотанной на одно из колес (рис. К2.0-К2.9, табл. К2). Радиусы ступеней равны соответственно: у колеса 2 – r2=6 см, R2=8 см, у колеса 3 – r3=12 см, R3 = 16 см. На ободьях колес расположены точки А и В. В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где: Определить в момент времени t 1 = 2 c указанные в таблице в столбцах «Найти» скорости (υ – линейные, ω – угловые) и ускорения (а – линейные, ε – угловые) соответствующих точек или тел (υ1 – скорость груза 1 и т.д.). Указания. Задача К2 – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны ременной передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы; при этом считается, что ремень по ободу колеса не скользит. Таблица К2
Пример К2. Рейка 1, ступенчатое колеса 2 с радиусами R2 и r2 и колесо 3 радиуса R3, скрепленное с валом радиуса r3, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К2). Рейка движется по закону s1=f(t). Дано: R2=6 см, r2=4 см, R3=8 см, r3=3 см, s1=3t3 (s- в сантиметрах, t – в секундах), А – точка обода колеса 3, t1 = 3 c. Определить: ω3, υ4, ε3, αA в момент времени t = t1.
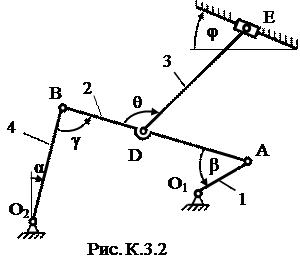
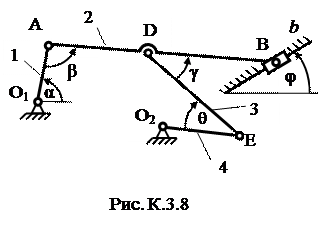
1. Определим сначала угловые скорости всех колес как функции времени t. Зная закон движения рейки 1, находим ее скорость Так как рейка и колесо 2 находятся в зацеплении, то υ2= υ1 или ω2R2= υ1. Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, u2= υ3 или ω2r2= ω3R3. Из этих равенств находим: Тогда для момента времени t1 = 3 c получим: ω3 =6,75c-1. 2. Определим υ4. Так как υ4 = υB = ω3r3, то при t1=3 c: υ4 =20,25 см/с. 3. Определяем ε3. Учитывая, что ε3= ε3=4,5 с-2. 4. Определяем aA. Для точки А: Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис. К2. Задача К3 Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е (рис. К3.0 – К3.7) или из стержней 1, 2, 3 и ползунов В и Е (рис. К3.8, К3.9), соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами; точка D находится в середине стержня АВ. Длина стержней: l 1 = 0,4 м, l 2 = 1,2 м, l 3 = 1,4 м, l 4 = 0,6 м. Положение механизма определяется углами α, β, γ, φ, θ. Значения этих углов и других заданных величин указаны в табл. К3а (для рис. 0-4) или в табл. К3б (для рис. 5-9); при этом в табл. К3а ω1 и ω4 – величины постоянные. Определить величины, указанные в таблицах в столбцах «Найти». Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол γ на рис. 8 следует отложить от DB по ходу часовой стрелки, а на рис. 9 – против хода часовой стрелки и т.д.). Построение чертежа начинать со стержня, направление которого определяется углом α; ползун с направляющими для большей наглядности изобразить так, как в примере К3 (см. рис. К3, б). Заданные угловую скорость и угловое ускорение считать направленными против хода часовой стрелки, а заданные скорость Указания. Задача К3 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности. При определении ускорений точек механизма исходить из векторного равенства Таблица К3а (к рис. К3.0 – К3.4)
Таблица К3б (к рис. К3.5 – К3.9)
Пример К3. Механизм (рис. К3, а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами. Дано: a=60º, b=150º, g=90º, j=30º, q=30º, AD = DB, l 1 = 0,4 м, l 2 = 1,2 м, l 3 = 1,4 м, w1 = 2 с-1, e1 = 7 с-2 (направление w1 и e1 – против хода часовой стрелки). Определить: uB, uE, w2, aB, e3. Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. К3, б). 2. Определяем uВ. Точка В принадлежит стержню АВ. Чтобы найти uВ, надо знать скорость какой-нибудь другой точки этого стержня и направление
Направление
3. Определяем
Чтобы вычислить С3D и C3B, заметим, что
Так как точка Е принадлежит одновременно стержню О2Е, вращающемуся вокруг О2, то 4. Определяем w2. Так как МЦС стержня 2 известен (точка С2) и
5. Определяем
Вектор Изображая на чертеже векторы
Таким образом, у величин, входящих в равенство (8), неизвестны только числовые значения a B и Чтобы определить a B, спроектируем обе части равенства (8) на направление АВ (ось х), перпендикулярное неизвестному вектору
Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что а В = 0,72 м/с2. (11) Так как а В > 0, то, следовательно, вектор 6. Определяем e3. Чтобы найти e3, сначала определим
Подставив в равенство (12) числовые значения всех величин из (11) и (7), найдем, что Теперь из равенства Ответ: uВ = 0,46 м/с; uЕ = 0,46 м/с; w2 = 0,67 с-1; а В = 0,72 м/с2; e3 = 2,56 с-2.
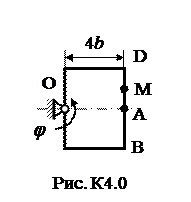
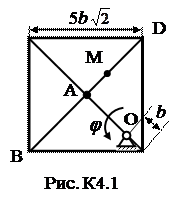
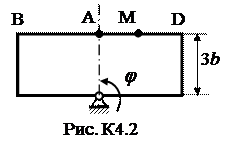
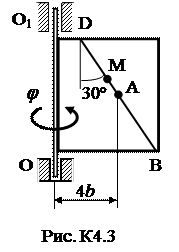
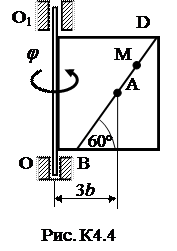
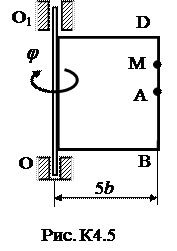
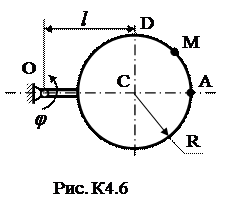
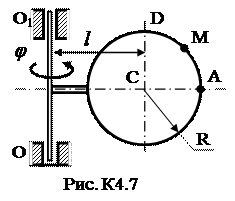
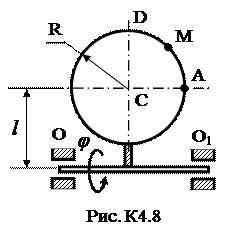
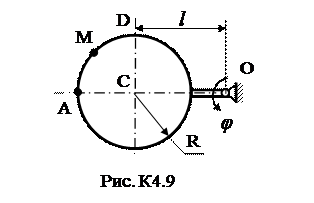
Задача К4 Прямоугольная пластина (рис. К4.0–К4.5) или круглая пластина радиуса R=60 см (рис. К4.6-К4.9) вращается вокруг неподвижной оси по закону j=f1(t), заданному в табл. К4. Положительное направление отсчета угла j показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 6, 9 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 5, 7, 8 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве). По пластине вдоль прямой BD (рис. 0-5) или по окружности радиуса R (рис. 6-9) движется точка М; закон ее относительного движения, т.е. зависимость s=AM=f2(t) (s выражено в сантиметрах, t - в секундах), задан в таблице отдельно для рис. 0-5 и для рис. 6-9; там же даны размеры b и l. На рисунках точка М показана в положении, при котором s = AM > 0 (при s < 0 точка М находится с противоположной стороны). Требуется определить скорость и ускорение точки в момент времени t1=1c. Указания. Задача К4 – на сложное движение точки. Для ее решения необходимо воспользоваться теоремами о сложении скоростей и ускорений при сложном движении. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка М на пластине в момент времени t 1=1c, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче). В случаях, относящихся к рис. 6-9, при решении задачи не подставлять числового значения R, пока не будут определены положение точки М в момент времени t 1=1 c (с помощью угла между радиусами СМ и СА в этот момент). ЗАМЕЧАНИЕ. В задачах на рис. 3,4,7,8 вектора
Таблица К4
Дано: R = 0,5 м, j = 2 t 3 - 4 t 2, s = (pR/6)(7 t – 2 t 2) (j – в радианах, s – в метрах, t – в секундах). Определить: uаб и ааб в момент времени t 1=1c. Решение. Рассмотрим движение точки М как сложное, считая ее движение по дуге ADB относительным, а вращение диска – переносным движением. Тогда абсолютная скорость
где, в свою очередь, Определим все характеристики относительного и переносного движений. 1. Относительное движение. Это движение происходит по закону: s = AM = (pR/6)(7 t – 2 t 2). (2) Сначала установим, где находится точка М на дуге ADB в момент времени t1. Полагая в уравнении (2) t = 1 c, получим:
Изображаем на рис. К4 точку М1 в положении, определяемом этим углом. Теперь находим числовые значения uОТ,
где: rОТ – радиус кривизны относительно траектории, т.е. дуги ADB. Для момента времени t 1 = 1c, учитывая, что R = 0,5 м, получим:
Знаки показывают, что вектор 2. Переносное движение. Это движение (вращение) происходит по закону: j = 2 t 3 - 4 t 2. Найдем угловую скорость ω и угловое ускорение ε переносного вращения: ω = Знаки указывают, что при t 1 = 1 c направление ε совпадает с направлением положительного отсчета угла φ, а направление ω ему противоположно; отметим это на рис. К4 соответствующими дуговыми стрелками. Тогда в момент времени t 1 = 1 c, учитывая равенства (4), получим:
Изображаем на рис. К4 и К4а векторы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 3412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.98.91 (0.009 с.) |

 , а r). Скорость и ускорение той точки подвижной системы, в которой находится движущаяся точка, по отношению к неподвижной системе называются переносными (v
, а r). Скорость и ускорение той точки подвижной системы, в которой находится движущаяся точка, по отношению к неподвижной системе называются переносными (v  , а
, а 
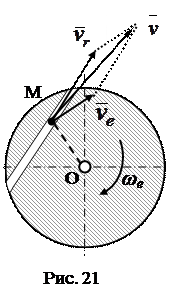 Например, на рис. 21 точка М совершает сложное движение: вращается вместе с диском – переносное движение, и двигается по хорде диска - относительное движение. При этом переносная скорость ve направлена перпендикулярно отрезку ОМ в сторону переносной угловой скорости ωe, а ее величина может быть найдена по формуле: ve = ωe ∙OM. Абсолютную скорость точки М можно найти по теореме косинусов:
Например, на рис. 21 точка М совершает сложное движение: вращается вместе с диском – переносное движение, и двигается по хорде диска - относительное движение. При этом переносная скорость ve направлена перпендикулярно отрезку ОМ в сторону переносной угловой скорости ωe, а ее величина может быть найдена по формуле: ve = ωe ∙OM. Абсолютную скорость точки М можно найти по теореме косинусов: 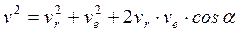 , где: α – угол между векторами ve и vr.
, где: α – угол между векторами ve и vr.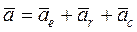 ,
,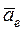 - переносное ускорение,
- переносное ускорение, 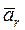 - относительное ускорение,
- относительное ускорение, 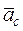 - ускорение Кориолиса:
- ускорение Кориолиса: 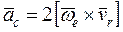 . модуль ускорения можно найти по формуле:
. модуль ускорения можно найти по формуле: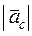 =2| ωe |∙|vr |∙sinβ, где: β – угол между векторами
=2| ωe |∙|vr |∙sinβ, где: β – угол между векторами 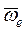 и
и 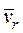 , в рассматриваемом случае этот угол равен 90º, так как вектор угловой скорости направлен перпендикулярно плоскости рисунка от нас. Для определения направления
, в рассматриваемом случае этот угол равен 90º, так как вектор угловой скорости направлен перпендикулярно плоскости рисунка от нас. Для определения направления 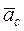 можно пользоваться, правилом векторного умножения или правилом Жуковского: для определения направления ускорения Кориолиса надо спроецировать вектор относительной линейной скорости на плоскость | оси переносного вращения и повернуть эту проекцию в этой плоскости на угол 90° в направлении переносной угловой скорости.
можно пользоваться, правилом векторного умножения или правилом Жуковского: для определения направления ускорения Кориолиса надо спроецировать вектор относительной линейной скорости на плоскость | оси переносного вращения и повернуть эту проекцию в этой плоскости на угол 90° в направлении переносной угловой скорости.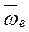 = 0; т.е. переносное движение будет поступательным.
= 0; т.е. переносное движение будет поступательным.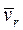 = 0; т.е. точка неподвижна по отношению к подвижной системе отсчета.
= 0; т.е. точка неподвижна по отношению к подвижной системе отсчета.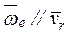 - точка движется параллельно оси переносного вращения.
- точка движется параллельно оси переносного вращения. (табл. К1) требуется найти уравнение траектории и для момента времени t1 = π/6 c определить скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории. Построить на рисунке все найденные скорости и ускорения в соответствующих масштабах.
(табл. К1) требуется найти уравнение траектории и для момента времени t1 = π/6 c определить скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории. Построить на рисунке все найденные скорости и ускорения в соответствующих масштабах.


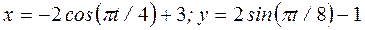 , (x, y – в сантиметрах, t - в секундах).
, (x, y – в сантиметрах, t - в секундах). или
или 
 Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим:
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим:
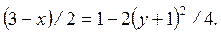


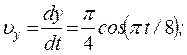




 .
. ax = 0,87 см/с2, ay = - 0,12 см/с2, a = 0,88 см/с2.
ax = 0,87 см/с2, ay = - 0,12 см/с2, a = 0,88 см/с2. . Получим:
. Получим: 
 Подставляя сюда найденные числовые значения a1 и a1τ, получим, что при t = 1 c: an = 0,58 см/с2.
Подставляя сюда найденные числовые значения a1 и a1τ, получим, что при t = 1 c: an = 0,58 см/с2. Подставляя сюда числовые значения υ 1 и a 1 n, найдем, что при t = 1 c: ρ = 3,05 см.
Подставляя сюда числовые значения υ 1 и a 1 n, найдем, что при t = 1 c: ρ = 3,05 см. , тогда:
, тогда:
 - закон вращения колеса 2, s4(t) – закон движения рейки 4, ω2(t) – закон изменения угловой скорости колеса 2, υ1(t) – закон изменения скорости груза 1 и т.д. (везде φ - выражено в радианах, s - в сантиметрах, t – в секундах). Положительное направление для φ и ω против хода часовой стрелки, для s1, s4 и υ1, υ4 – вниз.
- закон вращения колеса 2, s4(t) – закон движения рейки 4, ω2(t) – закон изменения угловой скорости колеса 2, υ1(t) – закон изменения скорости груза 1 и т.д. (везде φ - выражено в радианах, s - в сантиметрах, t – в секундах). Положительное направление для φ и ω против хода часовой стрелки, для s1, s4 и υ1, υ4 – вниз.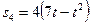
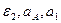









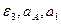




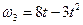
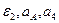
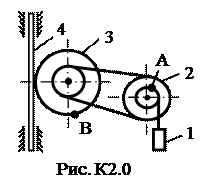
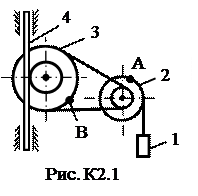





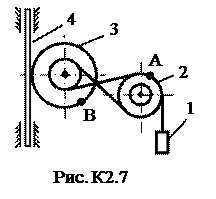


 Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса Ri), через υi, а точек, лежащих на внутренних ободах (радиуса ri), - через ui.
Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса Ri), через υi, а точек, лежащих на внутренних ободах (радиуса ri), - через ui. (1)
(1)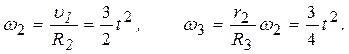
 = 1,5 t. Тогда при t 1=3 с получим:
= 1,5 t. Тогда при t 1=3 с получим: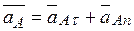 , где численно
, где численно  Тогда, для момента времени t1=3 с, имеем:
Тогда, для момента времени t1=3 с, имеем: 
 и ускорение
и ускорение  - от точки В к b (на рис. 5-9).
- от точки В к b (на рис. 5-9). , где А – точка, ускорение
, где А – точка, ускорение  которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то
которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то  ; В – точка, ускорение
; В – точка, ускорение 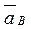 которой нужно определить (если точка В движется по дуге окружности радиуса l, то
которой нужно определить (если точка В движется по дуге окружности радиуса l, то  , где численно
, где численно  ; входящая сюда скорость υB определяется так же, как и скорости других точек механизма).
; входящая сюда скорость υB определяется так же, как и скорости других точек механизма).







 . По данным задачи, учитывая направление w1, можем определить
. По данным задачи, учитывая направление w1, можем определить  ; численно
; численно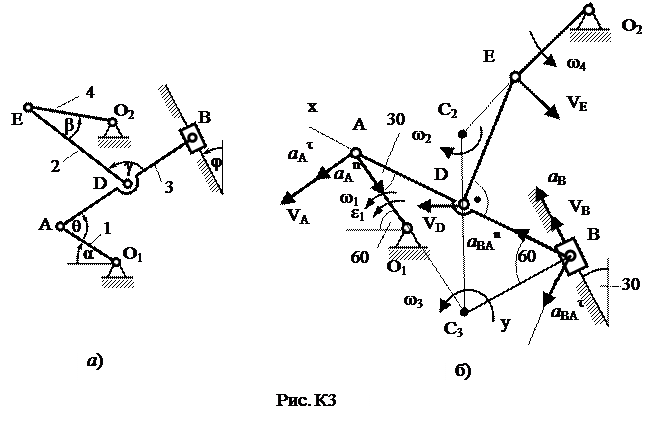
 (1)
(1) найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь зная
найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь зная  и направление
и направление  , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 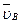 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим (2)
(2) . Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить
. Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить 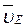 , надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная
, надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная  и
и  перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора 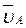 определяем направление поворота стержня АВ вокруг МЦС С3. Вектор
определяем направление поворота стержня АВ вокруг МЦС С3. Вектор  перпендикулярен отрезку С3D, соединяющему точки D и C3, и направлен в сторону поворота. Величину uD найдем из пропорции
перпендикулярен отрезку С3D, соединяющему точки D и C3, и направлен в сторону поворота. Величину uD найдем из пропорции (3)
(3)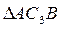 прямоугольный, так как острые углы в нем равны 30 и 60º, и что C3B=АВsin30º=0,5AB=BD. Тогда
прямоугольный, так как острые углы в нем равны 30 и 60º, и что C3B=АВsin30º=0,5AB=BD. Тогда 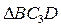 является равносторонним и C3B= С3D. В результате равенство (3) дает
является равносторонним и C3B= С3D. В результате равенство (3) дает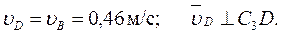 (4)
(4)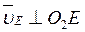 . Тогда, восставляя из точек Е и D перпендикуляры к скоростям
. Тогда, восставляя из точек Е и D перпендикуляры к скоростям 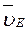 и
и 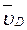 , построим МЦС С2 стержня DE. По направлению вектора
, построим МЦС С2 стержня DE. По направлению вектора 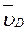 определяем направление поворота стержня DE вокруг центра С2. Вектор
определяем направление поворота стержня DE вокруг центра С2. Вектор 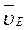 направлен в сторону поворота этого стержня. Из рис. К3,б видно, что
направлен в сторону поворота этого стержня. Из рис. К3,б видно, что 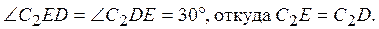 Составив теперь пропорцию, найдем, что:
Составив теперь пропорцию, найдем, что: 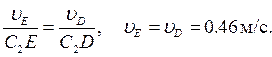 (5)
(5)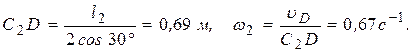 (6)
(6)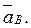 Точка В принадлежит стержню АВ. Чтобы найти
Точка В принадлежит стержню АВ. Чтобы найти 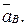 , надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить
, надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить 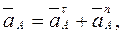 где числено:
где числено: (7)
(7)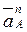 направлен вдоль АО1, а
направлен вдоль АО1, а 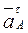 перпендикулярно ползуну, то вектор
перпендикулярно ползуну, то вектор 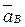 параллелен направляющим ползуна. Изображаем вектор
параллелен направляющим ползуна. Изображаем вектор 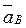 на чертеже, полагая, что он направлен в ту же сторону, что и
на чертеже, полагая, что он направлен в ту же сторону, что и 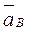 воспользуемся равенством:
воспользуемся равенством:  (8)
(8)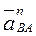 (вдоль ВА от В к А) и
(вдоль ВА от В к А) и 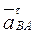 (в любую сторону перпендикулярно ВА); числено
(в любую сторону перпендикулярно ВА); числено 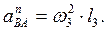 Найдя w3 с помощью построенного МЦС - С3 стержня 3, получим:
Найдя w3 с помощью построенного МЦС - С3 стержня 3, получим: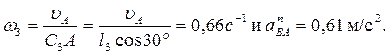 (9)
(9)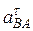 . Их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.
. Их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.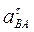 . Тогда получим:
. Тогда получим: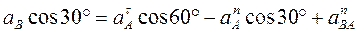 (10)
(10)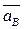 направлен, как показано на рис. К3, б.
направлен, как показано на рис. К3, б.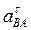 . Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим:
. Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим: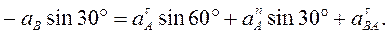 (12)
(12)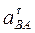 = -3,58 м/с2. Знак указывает, что направление
= -3,58 м/с2. Знак указывает, что направление 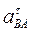 противоположно показанному на рис. К3, б.
противоположно показанному на рис. К3, б.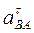 = e3 l3 получим:
= e3 l3 получим: 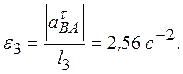
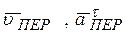 и
и 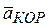 направлены перпендикулярно плоскости рисунка, поэтому в этих вариантах следует выбрать оси xyz, считая ось z направленной на нас. Направление на нас изображается значком
направлены перпендикулярно плоскости рисунка, поэтому в этих вариантах следует выбрать оси xyz, считая ось z направленной на нас. Направление на нас изображается значком  , а от нас:
, а от нас: 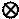 .
.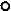

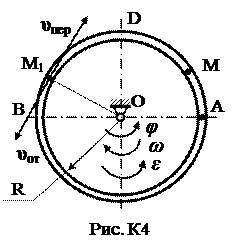 Пример К4. Диск радиуса R (рис. К4) вращается вокруг оси О перпендикулярной плоскости рисунка по закону j = f1(t) (положительное направление отсчета угла j показано на рис. К4 дуговой стрелкой.) По ободу ADB движется точка М по закону s = AM = f2(t); положительное направление отсчета s от A к D.
Пример К4. Диск радиуса R (рис. К4) вращается вокруг оси О перпендикулярной плоскости рисунка по закону j = f1(t) (положительное направление отсчета угла j показано на рис. К4 дуговой стрелкой.) По ободу ADB движется точка М по закону s = AM = f2(t); положительное направление отсчета s от A к D.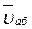 и абсолютное ускорение
и абсолютное ускорение 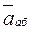 точки найдутся по формулам:
точки найдутся по формулам: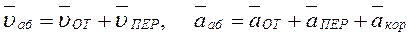 (1)
(1)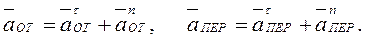
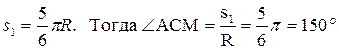 или
или 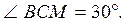
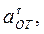
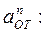
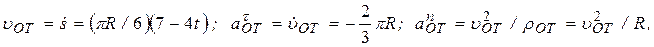
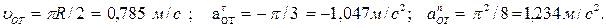 (3)
(3)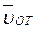 направлен в сторону положительно отсчета расстояния s, а вектор
направлен в сторону положительно отсчета расстояния s, а вектор 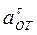 - в противоположную сторону;
- в противоположную сторону; 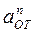 направлен к центру О дуги ADB. Изображаем все эти векторы на рис. К4 и К4а.
направлен к центру О дуги ADB. Изображаем все эти векторы на рис. К4 и К4а. = 6 t 2-8 t, ε =
= 6 t 2-8 t, ε = 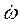 = 12 t - 8 и при t 1 = 1 c:
= 12 t - 8 и при t 1 = 1 c: 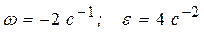 . (4)
. (4) (5)
(5) и
и  с уч
с уч 


