
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Сложное движение точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В главе введены понятия относительного, переносного и абсолютного движений точки, кориолисова ускорения, изложена методика определения скоростей и ускорений точки в сложном движении.
Скорость Скорость Движение точки Скорость Согласно теореме о сложении скоростей, абсолютная скорость точки
По теореме Кориолиса о сложении ускорений абсолютное ускорение точки
Кориолисово ускорение
Векторное равенство определяет модуль ускорения Кориолиса
где
Для определения направления ускорения Кориолиса Из выражений (3.4) вытекают условия, при выполнении которых ускорение Кориолиса равно 0.
Очевидно, 1) 2) 3) Рассмотрим характерные примеры решения задач на сложное движение точки.
Решение задач на сложное движение точки надо начинать с установления её относительного движения, далее найти переносное и наконец абсолютное движение. В некоторых задачах, к которым относится и данный пример, это можно сделать сразу без дополнительных исследований. Подробно определение движений приведено в примере 3. В рассматриваемом примере движение точки Находим положение точки
Абсолютная скорость точки равна
Переносная скорость
Относительная скорость точки равна
При
Абсолютное ускорение точки равно
Переносное ускорение
Так как относительное движение точки криволинейное, то относительное ускорение равно
Тогда
 . (3.7) . (3.7)
Находим модули и направляем составляющие абсолютного ускорения
Знак «минус» в
Ускорение Кориолиса
так как звено Поскольку все векторы составляющих абсолютного ускорения в рассматриваемом примере расположены в плоскости чертежа, для определения его модуля выбираем две любые перпендикулярные оси, например
Тогда
Пример 2. Точка
Относительная скорость Переносная скорость
где

Абсолютное ускорение точки равно
Так как переносное движение – вращательное, а относительное – криволинейное, то имеем
Переносное вращательное ускорение равно
Вектор Переносное центростремительное ускорение равно
Вектор Касательное ускорение
так как по условию задачи Нормальное ускорение
Вектор Ускорение Кориолиса Переносим вектор
Используя правило векторного произведения или правило Жуковского, находим, что вектор Выбираем систему перпендикулярных осей
Тогда абсолютное ускорение точки равно
 Пример 3. В кулисном механизме (рис. 41) кривошип Пример 3. В кулисном механизме (рис. 41) кривошип  вращается вокруг оси O с угловой скоростью вращается вокруг оси O с угловой скоростью  рад/с, угловым ускорением рад/с, угловым ускорением  рад/с² и приводит в движение кулису рад/с² и приводит в движение кулису  , вращающуюся вокруг оси , вращающуюся вокруг оси 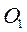 . .
  В этой задаче точка В этой задаче точка  совершает сложное движение: точка совершает сложное движение: точка  кривошипа ОА вращается вместе с ним вокруг оси О; точка А кулисы кривошипа ОА вращается вместе с ним вокруг оси О; точка А кулисы  , вращается вместе с ней вокруг оси , вращается вместе с ней вокруг оси 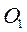 ; точка ; точка  ползуна движется вместе с ним по кулисе. ползуна движется вместе с ним по кулисе.
 , связанную с кулисой , связанную с кулисой  . Поскольку расстояние . Поскольку расстояние 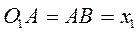 меняется при вращении кривошипа меняется при вращении кривошипа  , то, согласно определению относительного движения, движение ползуна , то, согласно определению относительного движения, движение ползуна  по кулисе по кулисе  есть движение относительное. Тогда вращение кулисы есть движение относительное. Тогда вращение кулисы  – движение переносное. Оставшееся движение – вращение точки вместе с кривошипом – движение переносное. Оставшееся движение – вращение точки вместе с кривошипом  – движение абсолютное. – движение абсолютное.
Абсолютная скорость точки
Определяем абсолютную скорость
 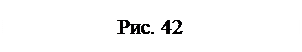  Из треугольника скоростей Из треугольника скоростей
тогда
 Указываем направление Указываем направление  . Записываем выражение для абсолютного ускорения точки . Записываем выражение для абсолютного ускорения точки 
Или с учётом вида абсолютного, переносного и относительного движений
Составляющие абсолютного ускорения, подчеркнутые в векторном равенстве (3.13) двумя чертами, известны по модулю и направлению, одной чертой – только по направлению.
Ускорение Кориолиса По модулю Используя правило Жуковского, указываем направление вектора Проектируем векторное равенство (3.13) на ось
Отсюда
Так как Тогда угловое ускорение кулисы O 1 B равно:
Ускорение Проектируя векторное равенство (3.13) на ось КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое сложное движение точки? 2. Что называется относительным, переносным и абсолютным движением? 3. Как определяется скорость точки при сложном движении? 4. Как определяется ускорение точки при сложном движении? 5. В каких случаях при сложном движении точки ускорение Кориолиса равно нулю?
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 843; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.069 с.) |

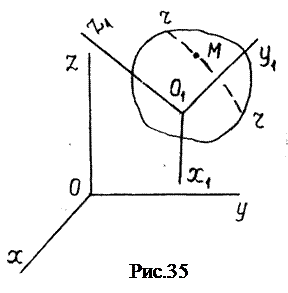 Точка
Точка  движется по некоторой траектории
движется по некоторой траектории  относительно тела
относительно тела  , обычно связанных с Землёй (рис. 35). Для изучения движения точки
, обычно связанных с Землёй (рис. 35). Для изучения движения точки  , связанную с телом. Движение точки
, связанную с телом. Движение точки  и ускорение
и ускорение  точки
точки  и ускорение
и ускорение  той точки тела
той точки тела  и ускорение
и ускорение  точки
точки  . (3.1)
. (3.1) ускорений
ускорений . (3.2)
. (3.2) равно удвоенному векторному произведению угловой скорости
равно удвоенному векторному произведению угловой скорости 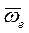 переносного движения на относительную скорость точки
переносного движения на относительную скорость точки  . (3.3)
. (3.3) , (3.4)
, (3.4)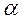 – меньший угол между векторами
– меньший угол между векторами  Из векторного произведения (3.3) следует, что ускорение Кориолиса
Из векторного произведения (3.3) следует, что ускорение Кориолиса  на угол 90° в направлении вращения переносной угловой скорости
на угол 90° в направлении вращения переносной угловой скорости 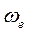 , получаем направление кориолисова ускорения
, получаем направление кориолисова ускорения  , если:
, если: ; учитывая, что
; учитывая, что  , где
, где  – угол поворота тела
– угол поворота тела  в двух случаях: а)
в двух случаях: а)  , то есть переносное движение является поступательным; б)
, то есть переносное движение является поступательным; б) 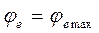 и
и 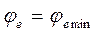 , угол поворота тела
, угол поворота тела  ; так как
; так как  , где
, где  – дуговая координата в относительном движении точки
– дуговая координата в относительном движении точки  также в двух случаях: а)
также в двух случаях: а)  (нет относительного движения точки); б)
(нет относительного движения точки); б)  и
и  (моменты изменения направления относительного движения точки);
(моменты изменения направления относительного движения точки);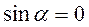 ; значит,
; значит,  , либо
, либо  , то есть это случай, когда векторы
, то есть это случай, когда векторы  Пример 1. Точка
Пример 1. Точка  м звена АВ механизма шарнирного четырёхзвенника
м звена АВ механизма шарнирного четырёхзвенника  по закону
по закону  ,
, 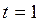 с, и в этом положении угловая скорость и угловое ускорение кривошипа
с, и в этом положении угловая скорость и угловое ускорение кривошипа  мравны
мравны  рад/с². Определить абсолютные скорость и ускорение точки
рад/с². Определить абсолютные скорость и ускорение точки 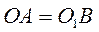 и
и 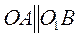 .
. – движение относительное, движение звена
– движение относительное, движение звена 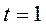 с
с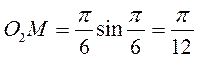 м, тогда
м, тогда  (рис. 38).
(рис. 38). ,
, м/с.
м/с.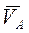 направлена
направлена  в сторону вращения
в сторону вращения  . Для угла
. Для угла  скорость
скорость  траектории относительного движения точки.
траектории относительного движения точки.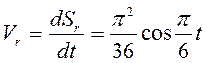 .
.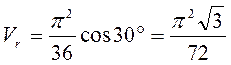 м/с.
м/с.
 м/с.
м/с. .
. .
.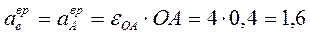 м/с²;
м/с²;  направлен
направлен  .
. м/с²;
м/с²;  направлен по
направлен по  .
. ; при
; при  м/с².
м/с². показывает, что вектор
показывает, что вектор  направлен в сторону уменьшения дуговой координаты
направлен в сторону уменьшения дуговой координаты  м/с².
м/с². м/с².
м/с².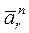 направлен по
направлен по  к центру
к центру 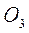 (рис. 38).
(рис. 38). ,
,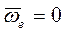 .
. ,и находим две проекции абсолютного ускорения на эти оси:
,и находим две проекции абсолютного ускорения на эти оси: м/с²,
м/с², м/с².
м/с². м/с².
м/с². м/с по жёлобу
м/с по жёлобу  м от
м от  . Пластина вращается вокруг оси
. Пластина вращается вокруг оси  ускоренно. В данный момент времени угловая скорость
ускоренно. В данный момент времени угловая скорость  рад/с, угловое ускорение
рад/с, угловое ускорение 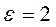 рад/с² и точка
рад/с² и точка 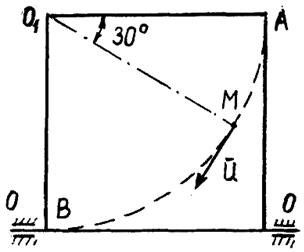 Для решения задачи зададим направление
Для решения задачи зададим направление  и
и  . Абсолютная скорость точки
. Абсолютная скорость точки  . Вектор
. Вектор 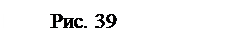
 ,
,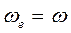 ),
), 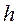 – радиус вращения той точки пластины, где находится точка М в данный момент времени.
– радиус вращения той точки пластины, где находится точка М в данный момент времени. м.
м. Тогда
Тогда  м/с.Вектор
м/с.Вектор 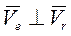 , то
, то . (3.10)
. (3.10) м/с².
м/с². направлен на нас.
направлен на нас. м/с².
м/с². направлен вниз.
направлен вниз. ,
, .
.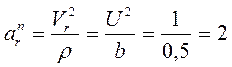 м/с².
м/с². . Вектор
. Вектор  м/с².
м/с². и находим три проекции абсолютного ускорения на выбранные оси:
и находим три проекции абсолютного ускорения на выбранные оси: м/с²;
м/с²; м/с²;
м/с²; м/с².
м/с². м/с².
м/с². Считая вращение кривошипа ускоренным, определить в заданном положении механизма угловую скорость и угловое ускорение кулисы
Считая вращение кривошипа ускоренным, определить в заданном положении механизма угловую скорость и угловое ускорение кулисы  ,
, 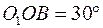 .
. . (3.11)
. (3.11) м/с.
м/с. м/с,
м/с,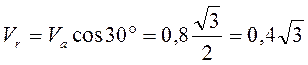 м/с,
м/с,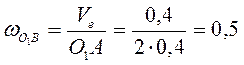 рад/с.
рад/с. . (3.13)
. (3.13) м/с²,
м/с²,  направлен по
направлен по  м/с²,
м/с², 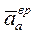 направлен
направлен  ;
; , так как относительное движение – прямолинейное, значит
, так как относительное движение – прямолинейное, значит 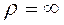 ;
; м/с², направлен по
м/с², направлен по  , от B к O 1.
, от B к O 1. м/с².
м/с². (перпендикулярно
(перпендикулярно  ) (рис. 42).
) (рис. 42).
 .
.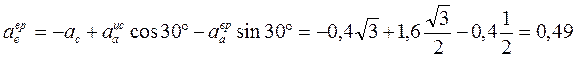 м/с².
м/с². получилось со знаком «+», то на рис. 42 указано верное направление вектора
получилось со знаком «+», то на рис. 42 указано верное направление вектора  рад/с².
рад/с². направлено в сторону, куда
направлено в сторону, куда  , можно найти относительное ускорение
, можно найти относительное ускорение 


