
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Основные положения и аксиомыСодержание книги
Поиск на нашем сайте
Ф.Г. БУДНИК, А.В. САКАЛО
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА: СТАТИКА, КИНЕМАТИКА
Утверждено редакционно-издательским советом университета в качестве учебного пособия
Брянск ИЗДАТЕЛЬСТВО БГТУ
Будник, Ф.Г. Теоретическая механика: Статика, кинематика [Текст]+[Электронный ресурс]: учеб. пособие / Ф.Г. Будник, А.В. Сакало; под общ. ред. Ф.Г. Будника. – Брянск: БГТУ, 2013. – 132 с.
ISBN 978-5-89838-688-7
Приводятся основные положения статики, кинематики и методика решения типовых инженерных задач по данным разделам теоретической механики. Учебное пособие предназначено для студентов очной и заочной форм обучения по всем машиностроительным направлениям подготовки бакалавров, а также может быть полезно для инженеров и преподавателей технических вузов.
Ил. 121. Библиогр. – 7 назв.
Научный редактор В.И. Сакало
Рецензенты: кафедра «Механика» Брянской государственной инженерно-технологической академии; зав. кафедрой, д.т.н., профессор И.Н. Серпик; академик РИА, д.т.н., профессор В.Т. Аксютенков
Редактор издательства О.З. Зрелова Компьютерный набор С.М. Васейкина, Р.И. Сергеенко
Темплан 2013 г., п. 10 Подписано в печать 14.05.13 Формат 60´84 1/16. Бумага офсетная. Офсетная печать. Усл.печ.л. 7,67 Уч.-изд.л. 7,67 Тираж 100 экз. Заказ
Издательство Брянского государственного технического университета 241035, Брянск, бульвар 50-летия Октября, 7, БГТУ. Тел. 58-82-49 Лаборатория оперативной полиграфии БГТУ, ул. Институтская, 16
ISBN 978-5-89838-688-7 ã Брянский государственный технический университет, 2013 ПРЕДИСЛОВИЕ
Данное пособие написано на базе учебного пособия [7]. Так как это пособие рассчитано на студентов машиностроительных специальностей, изучающих дисциплину теоретической механики по программам подготовки бакалавров, то его объём существенно сокращён. Из пособия издания 2004 г. убрана теория и примеры решения специализированных задач по статике и кинематике. В то же время некоторые главы пособия переработаны с учётом выявленных замечаний и неточностей, некоторые главы пособия расширены с учётом последних тенденций в преподавании теоретической механики. Так, в разделе «Статика» добавлена новая связь – скользящая опора.
Пособие предназначено для студентов первого и второго курсов очной и заочной форм обучения, изучающих теоретическую механику по машиностроительным направлениям подготовки бакалавров. Его можно использовать как для изучения теоретического материала, так и для проведения практических занятий. Учебное пособие отличается от основных известных учебников по теоретической механике порядком изложения теоретического материала, что позволяет более рационально использовать время, отводимое учебными планами на изучение разделов «Статика» и «Кинематика». Это особенно важно в связи с наметившейся тенденцией сокращения лекционных часов на изложение этих разделов. Предлагаемая в пособии методика решения задач даёт общий подход при решении примеров на практических занятиях и выполнении расчётно-графических работ. Эта методика отличается от общепринятых порядком выбора объектов исследования, расстановкой сил и составлением уравнений равновесия в статике. Пособие состоит из двух разделов. Каждый раздел делится на главы и параграфы. В конце каждой главы даются примеры решения задач, соответствующие изложенному в главе материалу, и приводятся контрольные вопросы. Каждая глава пособия представляет собой часть раздела, которую надо освоить обучающемуся для практического использования при решении соответствующих примеров и задач. Пособие дополняет основные учебники и учебные пособия по теоретической механике [1], [2], [3], [4], [5], [6], рекомендуемые при изучении разделов. При использовании данного пособия рекомендуется вначале изучить теоретический материал, изложенный в главе, далее разобрать приведенные в конце главы примеры. Ответы на контрольные вопросы позволяют оценить уровень освоения изложенного в главе материала. РАЗДЕЛ I. СТАТИКА
В первом разделе пособия излагаются основные положения теории статики и методика решения задач по статике.
ГЛАВА 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ И АКСИОМЫ СТАТИКИ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
В главе изложены основные понятия и аксиомы статики, рассмотрены наиболее часто встречаемые в задачах механики связи и возникающие в них реакции, дана теория и методика решения задач на систему сходящихся сил.
Предмет и задачи статики. Основные понятия статики
Статика – раздел механики, в котором изучаются законы равновесия материальных объектов. В статике решаются две задачи: 1. Преобразование действующих на объект систем сил в простейшие эквивалентные системы. 2. Установление условий равновесия материальных объектов, находящихся под действием системы сил. К основным понятиям статики относятся понятия материальной точки, абсолютно твёрдого тела и силы. Материальная точка – это тело, размерами которого можно пренебречь в условиях данной конкретной задачи.
Сила – физическая величина, выражающая количественную меру механического взаимодействия между телами. Сила Системой сил называют совокупность сил (
Систему сил называют уравновешенной или эквивалентной нулю, если она, будучи приложена к покоящемуся телу, не изменяет его состояния покоя. Такую систему сил обозначают Равнодействующей силой
Уравновешенной системы сил Действие системы сил на абсолютно твёрдое тело не изменится, если к ней присоединить или отбросить систему сил, эквивалентную нулю.
Следствие из аксиомы 3: действие данной силы на абсолютно твёрдое тело не изменится при переносе силы вдоль ее линии действия из точки А в точку В (рис. 2), т.е. в статике твёрдого тела сила – вектор скользящий.
4. Аксиома параллелограмма
Правило параллелограмма даёт геометрический способ определения равнодействующих двух пересекающихся сил:
Модуль равнодействующей можно определить, например, по теореме косинусов
но откуда
5. Аксиома равенства действия и противодействия
6. Аксиома затвердевания Равновесие деформированного тела под действием данной системы сил не изменится, если тело затвердеет (станет абсолютно твёрдым). Так, равновесие цепи не нарушится, если звенья цепи приварить друг к другу.
7. Аксиома отбрасывания связей (принцип освобождаемости) Твёрдое тело называется свободным, если оно может перемещаться в любом направлении пространства. Тела, ограничивающие свободу перемещения данного тела и делающие его несвободным, называются связями. В связях под действием приложенных к телу сил (активных сил) возникают усилия, называемые реакциями связей. Согласно принципу освобождаемости от связей, несвободное твёрдое тело можно рассматривать как свободное, если освободиться от связей, а их действие на тело заменить реакциями связей.
Рассмотрим наиболее часто встречаемые в задачах статики связи и возникающие в них реакции связей. 1. Гладкая (идеальная) поверхность (поверхность без трения) Реакция
2. Гибкая нить Реакция гибкой нити 3. Цилиндрический шарнир
Реакция 4. Сферический (пространственный) шарнир
Реакция 5. Подпятник В подпятнике (рис. 10), как и в сферическом шарнире, неизвестными являются три составляющие реакции 6. Невесомый стержень с шарнирами на концах
7. Плоская заделка Если действующие на балку АВ (рис. 12) силы В плоской заделке – три неизвестных: две составляющие
9. Скользящая опора Для бруса AB связь A – скользящая опора (рис. 14). В опоре A две неизвестных: реакция
Система сходящихся сил
Сходящейся называется такая система сил, в которой линии действия всех сил пересекаются в одной точке (например, в точке О на рис. 15).
На тело действует пространственная система сходящихся сил Перенося силы вдоль их линий действия в точку О, получим систему сил, приложенных в точке. Используя правило параллелограмма, геометрически суммируем силы, приложенные в точке О. В результате получаем, что сходящуюся систему сил можно заменить одной силой, равной геометрической сумме всех сил, приложенных в точке О, – равнодействующей
Правило параллелограмма для геометрического определения равнодействующей
Соединяя точку О с концом силы
Перенося Правило силового многоугольника можно рассматривать как многократное применение правила параллелограмма (рис. 16). Для равновесия сходящейся системы сил необходимо и достаточно, чтобы её равнодействующая
Геометрически условие (1.3) выражается в замкнутости силового многоугольника – конец последней силы
Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы их проекций на три координатные оси равнялись нулю. Аналитические условия равновесия плоской системы сходящихся сил определяются двумя уравнениями:
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы их проекций на две координатные оси равнялись нулю.
Теорема о трёх силах
На рис. 18 однородный шар весом Р подвешен на нити ВС и в точке А опирается на идеальную вертикальную поверхность. Так как реакция
Примеры решения задач на равновесие тел Пример 1
Решение 1. Объект равновесия – балка АВ. 2. Активные силы – Реакции связей: 3. Балка находится в равновесии под действием плоской системы сходящихся сил. Для такой системы необходимо выполнение условий равновесия (1.5). Однако если объект находится в равновесии под действием плоской системы трёх сходящихся сил, то вместо составления уравнений равновесия (1.5) задачу обычно рекомендуют решать графо-аналитическим способом. Геометрическое условие равновесия
В равенстве (1.6) вектор Равенство (1.6) содержит два неизвестных – модули
В треугольнике АОС
Из выражения (1.7) следует, что
Пример 2
Решение 1. Объект равновесия – узел А. 2. Активные силы: Реакции связей:
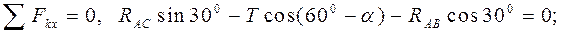
Из уравнений (1.8) с учётом того, что Т = Р, находим
Из первого выражения (1.9) следует, что при
Таким образом, при
Пример 3
Решение 1. Объект равновесия – узел А. 2. Активные силы: Реакции связей: 3. На узел А действует пространственная система сходящихся сил. Составляем три уравнения равновесия (1.4) для пространственной системы сходящихся сил:
Из выражений (1.10) получаем
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется связью? В чём заключается аксиома освобождаемости от связей? 2. Перечислите основные виды связей и возникающие в них реакции. 3. Что называется равнодействующей и главным вектором системы сил? 4. Как определяется направление равнодействующей системы сходящихся сил при построении силового многоугольника? 5. В чём выражается геометрическое условие равновесия плоской и пространственной систем сходящихся сил? 6. Каковы уравнения равновесия плоской и пространственной систем сходящихся сил? 7. Как читается теорема о равновесии тела под действием систем трёх непараллельных сил? ПРОИЗВОЛЬНЫЕ СИСТЕМЫ СИЛ
В главе даны понятия моментов силы относительно точки и оси, изложены основные положения теории и методики решения задач на плоскую и пространственную систему сил.
Пример
Решение Для определения момента силы
Знак "минус" момента взят потому, что сила Момент силы Для определения момента силы
Знак "плюс" момента взят потому, что сила
Пример Используя выражения (2.7), найти моменты силы Решение Из условия задачи находим координаты точки K приложения силы
Используя выражения (2.7), определяем моменты силы относительно координатных осей:
Пара сил и её момент
Парой сил называется система двух сил, равных по модулю, противоположных по направлению, действующих на некотором плече. Плечом пары d называется перпендикуляр, опущенный из точки приложения одной силы на линию действия другой.
Моментом пары сил m или
Момент пары имеет знак "+", если пара стремится вращать тело против хода часовой стрелки, "-" – по ходу. Свойства пары сил: 1) 2) равнодействующая сил пары 3) 4) момент сил пары относительно любой точки, взятой в плоскости действия пары, равен моменту пары.
5) из рис. 30
Момент пары как вектор
Из двух теорем об эквивалентных парах следует, что вектор
При этом справедливы векторные равенства:
Систем пар
Для равновесия пространственной системы пар необходимо и достаточно, чтобы момент результирующей пары (2.8) равнялся нулю
Аналитические условия равновесия пространственной системы пар получим, спроектировав векторное равенство (2.10) на три координатные оси:
Для равновесия пространственной системы пар необходимо и достаточно, чтобы суммы их проекций на три координатные оси равнялись нулю. С учётом того, что пары на плоскости суммируются алгебраически, аналитическое условие равновесия плоской системы пар получим, приравняв равенство (2.9) к нулю:
Для равновесия плоской системы пар необходимо и достаточно, чтобы их алгебраическая сумма равнялась нулю.
К одному центру
При приведении плоской произвольной системы сил к произвольному центру О получаем одну силу
и одну пару
Модуль
Тогда
Частные случаи приведения плоской системы сил к одному центру: 1. 2. 3. 4. Можно сделать вывод, что плоская произвольная система сил всегда приводится к равнодействующей, если не находится в равновесии (случай 1) и не приводится к одной паре (случай 3).
Систем сил
Для равновесия пространственной произвольной системы сил необходимо и достаточно, чтобы главный вектор системы
Геометрические условия равновесия (2.21) выражаются в замкнутости многоугольников сил и пар самих на себя. При выполнении условий (2.21) модули
Для равновесия пространственной произвольной системы сил необходимо и достаточно, чтобы суммы проекций сил на три координатные оси и суммы моментов сил относительно трех координатных осей равнялись нулю. Если на тело действует простра
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.171.188 (0.018 с.) |


 Абсолютно твёрдое тело – это тело, которое не деформируется под действием сил.
Абсолютно твёрдое тело – это тело, которое не деформируется под действием сил. – векторная величина, которая характеризуется тремя элементами: точкой приложения (точка А, рис. 1), линией действия и модулем (численным значением) силы
– векторная величина, которая характеризуется тремя элементами: точкой приложения (точка А, рис. 1), линией действия и модулем (численным значением) силы  .
.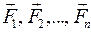 ), приложенных к телу. Две системы сил называются эквивалентными, если каждая из них, действуя отдельно, может сообщить покоящемуся телу одно и то же кинематическое состояние. Эквивалентные системы сил обозначают
), приложенных к телу. Две системы сил называются эквивалентными, если каждая из них, действуя отдельно, может сообщить покоящемуся телу одно и то же кинематическое состояние. Эквивалентные системы сил обозначают .
. .
. данной системы сил называют силу, эквивалентную этой системе сил:
данной системы сил называют силу, эквивалентную этой системе сил: .
.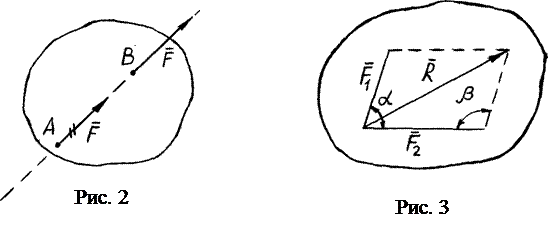 Равнодействующая двух пересекающихся сил проходит через точку их пересечения и определяется диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 3).
Равнодействующая двух пересекающихся сил проходит через точку их пересечения и определяется диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 3). .
. ;
; ,
,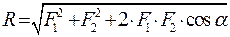 .
. Два материальных тела действуют друг на друга с силами, равными по модулю и направленными по одной прямой в противоположные стороны (рис. 4). Согласно аксиоме действия и противодействия, силы
Два материальных тела действуют друг на друга с силами, равными по модулю и направленными по одной прямой в противоположные стороны (рис. 4). Согласно аксиоме действия и противодействия, силы  . Однако система сил
. Однако система сил  не является уравновешенной, так как силы приложены к разным телам.
не является уравновешенной, так как силы приложены к разным телам. такой поверхности (рис. 5а) направлена по общей нормали к соприкасающимся поверхностям.
такой поверхности (рис. 5а) направлена по общей нормали к соприкасающимся поверхностям.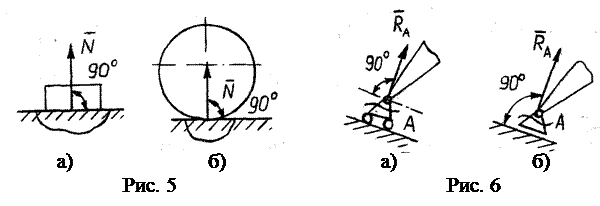 Если одна из поверхностей обращается в точку (рис. 5б), то реакция
Если одна из поверхностей обращается в точку (рис. 5б), то реакция  направлена по нормали ко второй поверхности. Отсюда следует, что реакция цилиндрической подвижной (катковой) опоры А
направлена по нормали ко второй поверхности. Отсюда следует, что реакция цилиндрической подвижной (катковой) опоры А  (рис. 6а) направлена по нормали к опорной поверхности. Иногда в задачах катковую опору изображают в виде "салазок" (рис. 6б).
(рис. 6а) направлена по нормали к опорной поверхности. Иногда в задачах катковую опору изображают в виде "салазок" (рис. 6б). направлена по нити к точке подвеса (рис. 7).
направлена по нити к точке подвеса (рис. 7).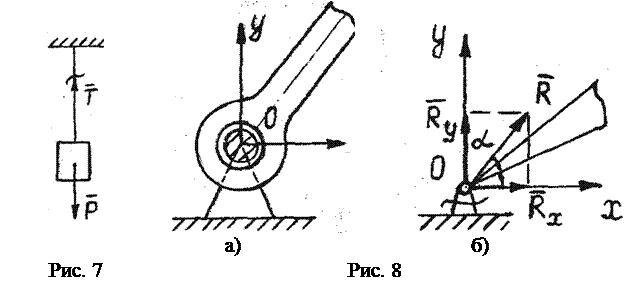 Эта связь не препятствует повороту тела в плоскости Оху, перпендикулярной оси шарнира (рис. 8а), но препятствует радиальному перемещению тела. В задачах обозначается, как показано на рис. 8б.
Эта связь не препятствует повороту тела в плоскости Оху, перпендикулярной оси шарнира (рис. 8а), но препятствует радиальному перемещению тела. В задачах обозначается, как показано на рис. 8б. и угол
и угол  , характеризующий направление её линии действия. Обычно вместо
, характеризующий направление её линии действия. Обычно вместо 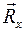 и
и  – составляющие реакции
– составляющие реакции 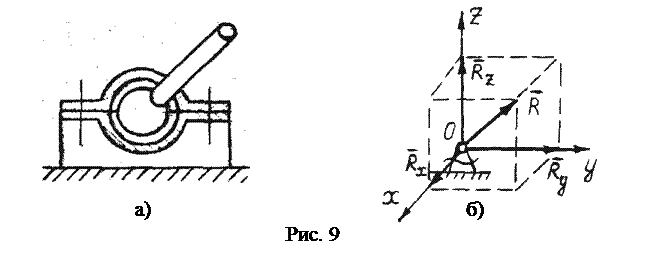 Сферический шарнир не препятствует повороту тела в пространстве (рис. 9а), в задачах обозначается так же, как и цилиндрический шарнир (рис. 9б).
Сферический шарнир не препятствует повороту тела в пространстве (рис. 9а), в задачах обозначается так же, как и цилиндрический шарнир (рис. 9б).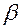 её наклона к осям Ох, Оу. Обычно вместо этих неизвестных вводят три составляющие
её наклона к осям Ох, Оу. Обычно вместо этих неизвестных вводят три составляющие 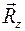 реакции
реакции  ,
,  и
и  .
.
 Реакция такого стержня СВ (рис. 11а)
Реакция такого стержня СВ (рис. 11а)  – стержень работает на сжатие (рис. 11б), если реакции направлены от узлов – на растяжение (рис. 11в).
– стержень работает на сжатие (рис. 11б), если реакции направлены от узлов – на растяжение (рис. 11в). расположены в плоскости балки (плоскость чертежа), в этом случае А – плоская заделка.
расположены в плоскости балки (плоскость чертежа), в этом случае А – плоская заделка. .
. 8. Пространственная заделка
8. Пространственная заделка Если действующие на балку АВ силы
Если действующие на балку АВ силы  .
. и момент
и момент 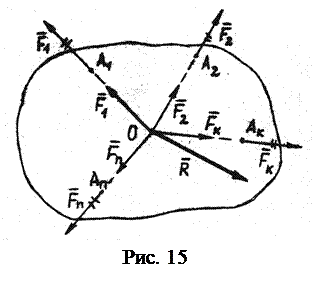 Могут быть плоская и пространственная системы сходящихся сил.
Могут быть плоская и пространственная системы сходящихся сил. . Силы приложены соответственно в точках
. Силы приложены соответственно в точках  , и их линии действия пересекаются в точке О.
, и их линии действия пересекаются в точке О. :
: . (1.1)
. (1.1)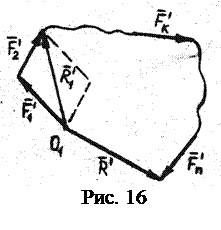 Вне основного чертежа (рис. 16) выбираем произвольную точку О 1 и в этой точке прикладываем силу
Вне основного чертежа (рис. 16) выбираем произвольную точку О 1 и в этой точке прикладываем силу  , геометрически равную силе
, геометрически равную силе 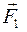
 . К концу силы
. К концу силы 
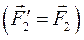 и т.д. до последней силы
и т.д. до последней силы 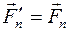 .
. , получим силу
, получим силу  , равную геометрической сумме всех сил и называемую главным вектором данной системы сил.
, равную геометрической сумме всех сил и называемую главным вектором данной системы сил. . (1.2)
. (1.2)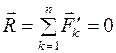 . (1.3)
. (1.3) совпадает с началом первой
совпадает с началом первой 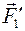 (с точкой О 1 на рис. 17).
(с точкой О 1 на рис. 17). Аналитические условия равновесия пространственной системы сходящихся сил (1.4) получаем, спроектировав векторное равенство (1.3) на три координатные оси:
Аналитические условия равновесия пространственной системы сходящихся сил (1.4) получаем, спроектировав векторное равенство (1.3) на три координатные оси: (1.4)
(1.4) . (1.5)
. (1.5)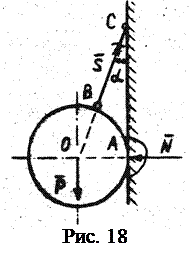 Если тело находится в равновесии под действием трёх сил и линии действия двух сил (например,
Если тело находится в равновесии под действием трёх сил и линии действия двух сил (например,  и
и  на рис. 18) пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
на рис. 18) пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке. должна проходить через точку О, поэтому на рис. 18 нить ВС должна совпадать с направлением ОС.
должна проходить через точку О, поэтому на рис. 18 нить ВС должна совпадать с направлением ОС. Балка АВ (рис. 19а) концом А крепится к основанию цилиндрическим шарниром, конец В – цилиндрическая подвижная (катковая) опора. В середине балки АВ под углом 45° к её оси действует сила
Балка АВ (рис. 19а) концом А крепится к основанию цилиндрическим шарниром, конец В – цилиндрическая подвижная (катковая) опора. В середине балки АВ под углом 45° к её оси действует сила  . Определить реакции опор.
. Определить реакции опор.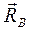 направлена перпендикулярно опорной поверхности, линия действия реакции
направлена перпендикулярно опорной поверхности, линия действия реакции  . (1.6)
. (1.6)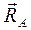 – одной чертой, ибо известны только направления их линий действия (направление указано в 1.6).
– одной чертой, ибо известны только направления их линий действия (направление указано в 1.6).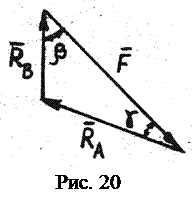 Построением силового треугольника (рис. 20) завершается графическое решение равенства (1.6). Аналитический этап в графоаналитическом способе заключается в геометрическом решении треугольника сил. Треугольник сил (рис. 20) и треугольник ОАС на рис. 19б подобны (как треугольники с параллельными сторонами). Из подобия треугольников следует
Построением силового треугольника (рис. 20) завершается графическое решение равенства (1.6). Аналитический этап в графоаналитическом способе заключается в геометрическом решении треугольника сил. Треугольник сил (рис. 20) и треугольник ОАС на рис. 19б подобны (как треугольники с параллельными сторонами). Из подобия треугольников следует . (1.7)
. (1.7)

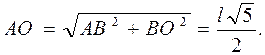


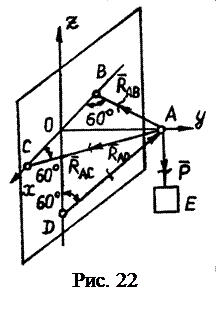
 Груз Е (рис. 21) весом Р поднимается лебёдкой D при помощи троса DАЕ, перекинутого через блок А. Пренебрегая трением троса о блок, найти реакции невесомых стержней АВ и АС в зависимости от угла a. Определить, при каком угле a усилие стержня АВ равно нулю.
Груз Е (рис. 21) весом Р поднимается лебёдкой D при помощи троса DАЕ, перекинутого через блок А. Пренебрегая трением троса о блок, найти реакции невесомых стержней АВ и АС в зависимости от угла a. Определить, при каком угле a усилие стержня АВ равно нулю. ,
,  (направлены по стержням),
(направлены по стержням),  . Так как А – идеальный блок, то Т = Р. Учитывая, что на узел А действует плоская система сходящихся сил и общее число действующих сил больше трёх, составляем два уравнения равновесия (1.5):
. Так как А – идеальный блок, то Т = Р. Учитывая, что на узел А действует плоская система сходящихся сил и общее число действующих сил больше трёх, составляем два уравнения равновесия (1.5):
 (1.9)
(1.9) получаем
получаем
 .
. Определить усилия (рис. 22) невесомых стержней АВ, АС, АD, которые идеальным шарниром скреплены в точке А и идеальными шарнирами В, С, D крепятся к вертикальной стене. К узлу А подвешен груз Е весом Р.
Определить усилия (рис. 22) невесомых стержней АВ, АС, АD, которые идеальным шарниром скреплены в точке А и идеальными шарнирами В, С, D крепятся к вертикальной стене. К узлу А подвешен груз Е весом Р. ,
,  .
. (1.10)
(1.10)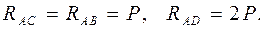
 По диагонали KN (рис. 27) параллелепипеда, размеры которого указаны на рис. 27, действует сила F = 10 Н. Найти моменты этой силы относительно координатных осей.
По диагонали KN (рис. 27) параллелепипеда, размеры которого указаны на рис. 27, действует сила F = 10 Н. Найти моменты этой силы относительно координатных осей. и находим момент составляющей
и находим момент составляющей 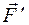 относительно точки О – точки встречи оси Ox с плоскостью Oух
относительно точки О – точки встречи оси Ox с плоскостью Oух (H×м).
(H×м). , так как сила
, так как сила  и находим момент составляющей
и находим момент составляющей  относительно точки О – точки встречи оси Oz с плоскостью Oxy
относительно точки О – точки встречи оси Oz с плоскостью Oxy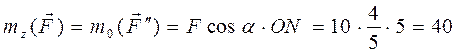 (Н×м).
(Н×м).
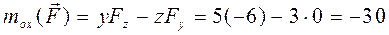 (Н×м);
(Н×м); ;
;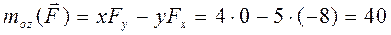 (Н×м).
(Н×м). Плоскость, проведенная через линии действия сил пары, называется плоскостью действия пары (рис. 30).
Плоскость, проведенная через линии действия сил пары, называется плоскостью действия пары (рис. 30). называется скалярная величина, равная взятому с соответствующим знаком произведению модуля силы на плечо пары:
называется скалярная величина, равная взятому с соответствующим знаком произведению модуля силы на плечо пары:
 не меняется при переносе сил пары вдоль их линий действия;
не меняется при переносе сил пары вдоль их линий действия; ;
; ;
; Так, для пары сил (рис. 31)
Так, для пары сил (рис. 31)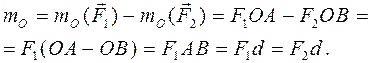

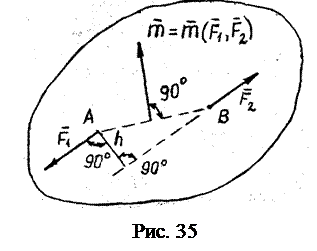 Момент пары
Момент пары 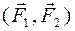 изображают в виде вектора
изображают в виде вектора 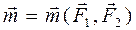 (pиc. 35), который перпендикулярен плоскости действия пары и направлен в ту сторону, откуда вращение пары представляется происходящим против хода часовой стрелки.
(pиc. 35), который перпендикулярен плоскости действия пары и направлен в ту сторону, откуда вращение пары представляется происходящим против хода часовой стрелки.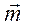 можно переносить параллельно самому себе и вдоль линии действия, т.е. вектор момента пары
можно переносить параллельно самому себе и вдоль линии действия, т.е. вектор момента пары  является свободным. Модуль
является свободным. Модуль  вектора пары
вектора пары  .
.
 . (2.10)
. (2.10)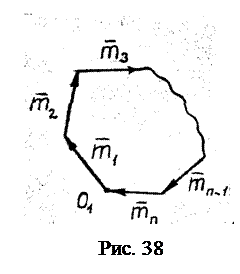 Геометрические условия равновесия (2.10) выражаются в замкнутости многоугольника пар самого на себя (рис. 38): конец последнего вектора
Геометрические условия равновесия (2.10) выражаются в замкнутости многоугольника пар самого на себя (рис. 38): конец последнего вектора  приходит в начало первого.
приходит в начало первого. . (2.11)
. (2.11)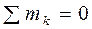 . (2.12)
. (2.12)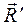 , равную геометрической сумме сил системы и называемую главным вектором системы сил
, равную геометрической сумме сил системы и называемую главным вектором системы сил , (2.18)
, (2.18) , называемую главным моментом системы сил относительно центра приведения О. Учитывая, что при параллельном переносе сил моменты присоединяемых согласно лемме Пуансо пар для плоской системы сил находятся в плоскости действия сил системы, а пары на плоскости суммируются алгебраически, получаем, что для плоской системы сил главный момент относительно центра О равен алгебраической сумме моментов сил системы относительно центра О:
, называемую главным моментом системы сил относительно центра приведения О. Учитывая, что при параллельном переносе сил моменты присоединяемых согласно лемме Пуансо пар для плоской системы сил находятся в плоскости действия сил системы, а пары на плоскости суммируются алгебраически, получаем, что для плоской системы сил главный момент относительно центра О равен алгебраической сумме моментов сил системы относительно центра О: (2.19)
(2.19)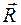 главного вектора
главного вектора  . (2.20)
. (2.20)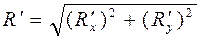 ,
, .
. – система сил находится в равновесии.
– система сил находится в равновесии. – система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О.
– система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О. – система приводится к паре сил, момент которой не зависит от выбора центра приведения О.
– система приводится к паре сил, момент которой не зависит от выбора центра приведения О. . Учитывая, что для плоской системы сил вектор главного момента
. Учитывая, что для плоской системы сил вектор главного момента  относительно любого центра приведения О всегда перпендикулярен
относительно любого центра приведения О всегда перпендикулярен  , этот случай приведения плоской системы сил аналогичен случаю 4 приведения пространственной системы сил (
, этот случай приведения плоской системы сил аналогичен случаю 4 приведения пространственной системы сил (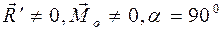 ), значит, в этом случае плоская система сил приводится к равнодействующей.
), значит, в этом случае плоская система сил приводится к равнодействующей. . (2.21)
. (2.21) и
и  , если каждое из слагаемых под радикалом в выражении (2.15) равно нулю. Аналогично
, если каждое из слагаемых под радикалом в выражении (2.15) равно нулю. Аналогично  , если каждое слагаемое под радикалом в выражении (2.17) равно нулю. Отсюда получаем шесть уравнений (2.22), характеризующих аналитические условия равновесия пространственной произвольной системы сил:
, если каждое слагаемое под радикалом в выражении (2.17) равно нулю. Отсюда получаем шесть уравнений (2.22), характеризующих аналитические условия равновесия пространственной произвольной системы сил: (2.22)
(2.22)


