
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Фермы. Равновесие тел с учётом тренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В главе рассмотрены методы расчёта ферм, равновесие тел с учётом трения скольжения и трения качения и приведены примеры решения задач с учётом трения.
Фермы
Фермой называется неизменяемая конструкция, состоящая из стержней (рис. 51). Основу фермы составляют геометрически неизменяемая фигура – треугольник.
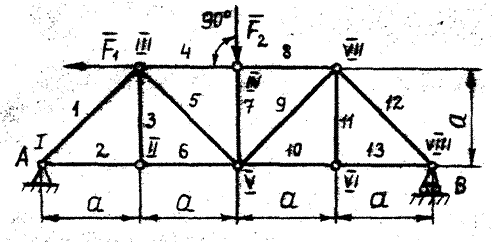
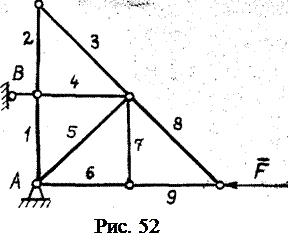
Задача расчёта фермы включает определение опорных реакций и усилий в стержнях фермы. При расчёте фермы вводятся следующие допущения: 1. Стержни в узлах фермы соединены идеальными шарнирами. 2. Весом стержней либо пренебрегают, либо разносят по узлам фермы. 3. Действующие на ферму силы приложены в узлах фермы. При выполнении этих условий стержни фермы будут испытывать только сжимающие или растягивающие нагрузки. Причём если реакция стержня на узел направлена к узлу, то стержень сжат, если от узла – растянут (здесь аналогия с реакциями невесомого стержня на рис. 11). Стержни, усилия в которых при заданных внешних силах равны нулю, называются нулевыми. Можно указать три признака наличия нулевых стержней в плоской ферме (леммы о нулевых стержнях). 1. Если в узле сходятся три стержня, на узел не действуют внешние силы и два стержня находятся на одной прямой, то третий стержень нулевой. По этой лемме усилия в стержнях 3 и 11 фермы на рис. 51 равно нулю. 2. Если в узле сходятся два стержня и узел не загружен внешними силами, то оба стержня нулевые (например, стержни 2 и 3 на рис. 52). 3. Если в узле сходятся два стержня и действующая на узел сила направлена по одному из них, то второй стержень нулевой (стержень 8 на рис. 52).
Для определения усилий в стержнях фермы обычно применяют метод вырезания узлов и метод Риттера. Рассмотрим эти два метода на примере фермы, изображенной на рис. 51. Расчёт фермы любым методом начинается с определения опорных реакций. 1. Объект равновесия – ферма (рис. 53).
2. Внешние силы: Пусть Реакции связей: 3. На ферму действует плоская произвольная система сил. Составляем три уравнения равновесия:
Метод вырезания узлов Вырезаем узел, в котором сходятся два стержня (либо узел I, либо – VIII), например, узел I (рис. 54). Усилия
Так как усилие Далее выделяем узел, где имеется два новых стержня – узел II (рис. 55). К узлу II прикладываем усилия
Далее последовательно вырезаем узлы III, IV, V, VI, VII, VIII. Следует oтмeтить, чтo при выделении пocлeднero узла VIII усилия в стержнях 12 и 13 будут уже определены при рассмотрении узлов VI, VII, поэтому два уравнения равновесия для этого узла можно считать проверочными. При правильном определении усилий в стержнях фермы уравнения равновесия для узла VIII должны дать тождество 0=0. Метод Риттера Этот метод позволяет определить усилие в любом стержне фермы без определения усилий в других стержнях. В этом преимущество этого метода перед методом вырезания узлов. Усилия в стержнях фермы по методу Риттера определяются после определения опорных реакций. Используя метод Риттера, определим, например, усилия в стержнях 4, 5, 6 фермы на рис. 53. Для этого разрезаем ферму на две части сечением b-b (рис. 53) так, чтобы были разрезаны стержни, усилия в которых надо определить. Общее число разрезанных стержней не должно превышать трёх (в соответствии с тремя уравнениями равновесия для плоской произвольной системы сил). Для дальнейшего рассмотрения можно взять любую часть фермы, например левую (рис. 56). К выделенной части фермы прикладываем действующие на неё силы

Трение скольжения
Очевидно, если Q = 0, то и сила трения I. Сила трения направлена по общей касательной к соприкасающимся поверхностям в сторону, противоположную направлению возможного смещения тела. II. Сила трения не зависит от площади поверхности контакта тел и не превышает некоторое предельное значение
III. Предельное значение силы трения пропорционально нормальной реакции поверхности N:
где IV. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей (шероховатости, влажности, температуры, смазки и т.д.).
Угол
Чтобы тело оставалось в покое, необходимо
 Значит, Значит, 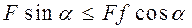 . Откуда . Откуда 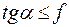 , но , но  , поэтому , поэтому 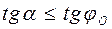 , т.е. , т.е. 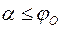 (условие покоя тела при действии силы (условие покоя тела при действии силы 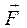 ). При выполнении условия ). При выполнении условия 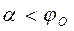 происходит самоторможение тела: сила, приложенная внутри конуса трения, не может сдвинуть тело с места при любой её величине. происходит самоторможение тела: сила, приложенная внутри конуса трения, не может сдвинуть тело с места при любой её величине.
Задачи на равновесие тел с учётом трения скольжения решаются аналогично задачам, в которых на тела действует плоская произвольная система сил. Необходимо только ко всем действующим на тело силам прибавлять силу трения.
Пример
Тело весом Р (рис. 60) поднимается вверх по наклонной плоскости под действием силы
Решение 1. Объект равновесия – тело. 2. Активные силы: 3. На тело действует плоская произвольная система сил:
 (3.1) (3.1)
Сила трения
Подставляем уравнение (3.2) в выражение (3.1)
Подставляем уравнение (3.4) в формулу (3.3)
Очевидно, Следовательно, Из выражения (3.5)
Трение качения
где k – коэффициент трения качения, измеряется в единицах длины. На рис. 61 силы Чтобы каток катился, момент движущей пары должен быть больше (либо равен) пары момента трения качения:
Чтобы каток катился без скольжения, сила Q не должна превышать предельного значения силы трения скольжения, значит,
Следовательно, Полученное соотношение подтверждает, что каток легче катить, чем перемещать без качения. Так, переход в железнодорожном транспорте от подшипников скольжения на подшипники качения позволяет уменьшить движущую силу, которую должен развивать локомотив, чтобы двигать состав вагонов. Пример
Решение 1. Объект равновесия – каток. 2. Активные силы: Реакции связей: сила трения скольжения 3. Для определения силы Q составим уравнение равновесия
Отсюда
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какая конструкция называется фермой? 2. Какие допущения вводятся при расчёте ферм? 3. В чём выражаются методы вырезания узлов и Риттера для определения усилий в стержнях фермы? 4. Что такое нулевые стержни и каковы признаки их наличия в ферме? 5. На каких законах базируется изучение трения скольжения и как читаются эти законы? 6. Что такое коэффициент трения скольжения? 7. Что называется конусом трения? 8. В чём выражается условие самоторможения тела? 9. Какова сущность трения качения? Что такое коэффициент трения качения? 10. Почему круглое тело легче катить, чем перемещать без качения?
ГЛАВА 4. ЦЕНТР ТЯЖЕСТИ
В главе рассмотрены определения равнодействующей системы параллельных сил и координат их центра, а также центра тяжести тела и приведены примеры на определение координат центров тяжести однородных тел.
Центр параллельных сил
Найдём равнодействующую
Равнодействующая
Так как
Затем найдём равнодействующую
Применив для сил
Продолжая дальше сложение сил, получим, что модуль равнодействующей R системы параллельных сил равен алгебраической сумме их модулей:
Равнодействующая Из выражений (4.1) – (4.5) следует, что при повороте в пространстве всех сил системы на один и тот же угол (например, на угол α) получим систему вертикальных сил Отсюда вытекает основное свойство центра параллельных сил: его положение в пространстве не меняется при повороте всех сил системы на один и тот же угол. Центром параллельных сил называется точка С, в которой приложена равнодействующая системы параллельных сил и положение которой не меняется при повороте всех сил системы в пространстве на один и тот же угол. На рис. 63 показаны координаты Для определения координат центра параллельных сил С воспользуемся теоремой Вариньона о моменте равнодействующей. Запишем эту теорему для вертикальных сил
откуда Относительно оси Ох:
откуда Для определения координаты
откуда Таким образом, координаты центра параллельных сил равны
Центр тяжести твёрдого тела
Тело А (рис. 64) находится в однородном поле сил тяготения. Разбиваем это тело на бесконечно малые тела
Точка С, в которой приложен вес тела
Согласно основному свойству центра параллельных сил, положение центра тяжести С относительно тела А не меняется при повороте тела в пространстве. Следовательно, центром тяжести тела называется точка С, в которой приложен вес тела Р и положение которой относительно тела не меняется при повороте тела в пространстве. Координаты центра тяжести С найдём, используя выражения (4.6) для координат центра параллельных сил:
В общем случае для определения координат центра тяжести тела используют выражения (4.7). Однако если тела однородные, то эти выражения можно упростить.
1. Однородный объём Обозначим через Тогда вес k -го элемента тела с объёмом
Подставляя значения Р, РК в выражения (4.7), получаем координаты центра тяжести однородного объёма:
где Если тело не разбивается на отдельные тела, координаты центров тяжести которых известны, то разбиваем тело на бесконечно малые объёмы
В выражениях (4.9) интегрирование осуществляется по всему объёму V. 2. Однородная площадь Совмещаем тело с плоскостью Oxy. В этом случае координата центра тяжести тела Пусть
Подставляя
Из выражений (4.10) получаем
Выражения (4.11) называются статическими моментами площади относительно осей Oy и Ox соответственно. Если начало отсчёта О системы осей Oxy совместить с центром тяжести – точкой С, то в этом случае координаты центра тяжести тела
Следовательно, статический момент площади относительно любой оси, проходящей через центр тяжести тела, равен нулю. Если плоское тело не разбивается на отдельные тела, координаты центров тяжести которых известны, то в этом случае по аналогии с выражениями (4.9) получаются выражения интегрального вида:
В выражениях (4.12) интегрирование проводится по площади тела S. 3. Однородная линия Разбиваем тело на ряд тел, координаты центров тяжести известны. Обозначим через
Подставляя значения
Если линия не разбивается на отдельные тела, координаты центров тяжести которых известны, то в этом случае по аналогии с выражениями (4.9) и (4.12) получаются интегральные выражения:
В выражениях (4.14) интегрирование осуществляется по всей длине линии L, т.е. это криволинейные интегралы. 4. Замечание о симметрии тела Пусть тело имеет плоскость симметрии, которую совмещаем с плоскостью Oxy (рис. 65). Ввиду симметрии каждому элементу тела vk с координатой zk (расположенному над плоскостью симметрии) соответствует такой же элемент vk с координатой zk, который расположен под плоскостью симметрии. В этом случае в выражениях (4.8) координата
1. Если тело имеет плоскость симметрии, его центр тяжести находится в этой плоскости. 2. Если тело имеет две плоскости симметрии, его центр тяжести находится на линии их пересечения. 3. Если тело имеет три плоскости симметрии, его центр тяжести находится в точке их пересечения. Рассмотрим примеры определения координат центров тяжести некоторых однородных тел.
Пример 1
Совмещаем ось Ох (рис. 66) с осью симметрии дуги АВ. Тогда координата
Выделяем на центральном угле j бесконечно малую дугу dl с центральным углом
Подставляя эти значения в выражение (4.15), получаем:
Следовательно, координата
где a – половина центрального угла дуги в радианах.
Пример 2 Центр тяжести треугольника. Разбиваем треугольник (рис. 67) на бесконечно тонкие полоски, параллельные стороне АД. Так как полоски имеют бесконечно малую ширину, можно считать, что их центры тяжести находятся на середине длинных сторон полосок. Следовательно, центры тяжести таких полосок находятся на меридиане ВК.
При этом очевидны соотношения:
Пример 3 Центр тяжести однородного сектора с центральным углом 2a и радиусом R.
Выделяем из сектора элементар-ный сектор с бесконечно малым углом Используя выражение (4.16) для центра тяжести дуги, получаем координаты центра тяжести однородного сектора:
В выражении (4.17) α – половина центрального угла сектора, выражается в радианах.
Пример 4 Определить координаты центра тяжести однородного плоского тела (рис. 69), которое получается, если из квадрата 1 со стороны Задачу решаем методом отрицательных площадей.
1. Квадрат без выреза
2. Четверть круга с отрицательной площадью
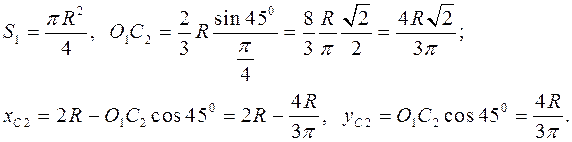
3. Треугольник
Находим координаты центра тяжести тела
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется центром параллельных сил? Каково его основное свойство? 2. По каким формулам вычисляются координаты центра параллельных сил? 3. Что называется центром тяжести тела? 4. Как определяются координаты центра тяжести тела в общем случае? 5. По каким формулам вычисляются координаты центров тяжести однородных объёмных тел, плоских фигур и линий? 6. Что называется статическим моментом площади плоской фигуры относительно оси? Как он вычисляется? Какую размерность имеет? 7. В чём сущность метода отрицательных площадей при определении координат центров тяжести плоских тел? РАЗДЕЛ II. КИНЕМАТИКА
Во втором разделе пособия излагаются основные положения теории кинематики и методика решения задач по кинематике. Как и в первом разделе пособия "Статика", в разделе «Кинематика» объём изложенной в пособии теории соответствует тому объёму знаний по кинематике, который должны иметь студенты для решения задач и выполнения расчётно-графических работ по данному разделу, поэтому основные теоремы кинематики излагаются без вывода и даются пояснения по практическому применению этих теорем. Некоторые разделы кинематики излагаются в пособии достаточно подробно и могут быть рекомендованы для самостоятельного изучения. Кинематика – раздел теоретической механики, в котором изучается движение материальных объектов без учёта их масс и действующих на них сил. В нём изучается простейшая форма движения материи – механическое движение, то есть происходящее во времени изменение положения одного материального объекта относительно другого, с которым связывается система отсчёта. В кинематике рассматриваются две основные задачи. Первая задача – установление закона движения объекта, т.е. такого математического описания движения, которое определяет положение движущегося объекта в пространстве. Вторая задача – определение по известному закону движения объекта основных кинематических характеристик движения. В зависимости от вида рассматриваемых объектов различают кинематику точки, кинематику твёрдого тела и кинематику сплошной среды.
ГЛАВА 1. КИНЕМАТИКА ТОЧКИ
В главе изложены основные положения теории и методика решения задач по кинематике точки.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 848; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.120 (0.016 с.) |

 Справедливость указанных признаков можно доказать, например, используя для определения усилий в стержнях фермы метод вырезания узлов.
Справедливость указанных признаков можно доказать, например, используя для определения усилий в стержнях фермы метод вырезания узлов.
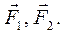
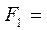 10 кН,
10 кН, 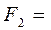 20 кН.
20 кН.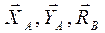 .
.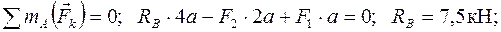

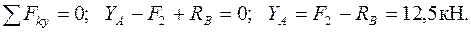
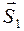 и
и  в разрезанных стержнях 1, 2 направляем вначале от узлов, т.е. считаем, что стержни растянуты. К узлу прикладываем действующие на него усилия
в разрезанных стержнях 1, 2 направляем вначале от узлов, т.е. считаем, что стержни растянуты. К узлу прикладываем действующие на него усилия 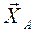 и
и  .
. Составляем два уравнения равновесия для плоской системы сходящихся сил:
Составляем два уравнения равновесия для плоской системы сходящихся сил: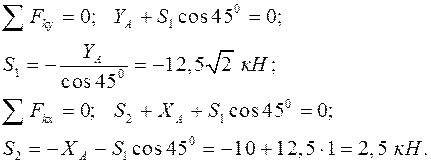
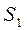 получилось со знаком «минус», то стержень I сжат.
получилось со знаком «минус», то стержень I сжат.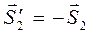 (согласно аксиоме действия-противодействия),
(согласно аксиоме действия-противодействия), 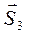 и
и 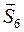 . Составляем два уравнения равновесия:
. Составляем два уравнения равновесия:
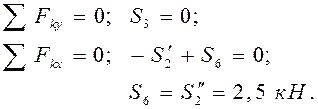
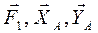 .
.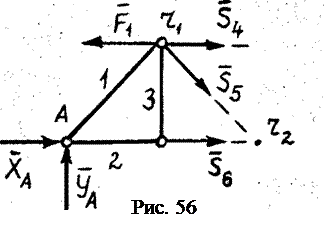 Усилия в разрезанных стержнях
Усилия в разрезанных стержнях 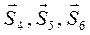 направляем вначале от узлов, т.е. считаем, что стержни растянуты. Составляем три уравнения равновесия для плоской произвольной системы сил, действующих на выделенную часть. Уравнения равновесия в методе Риттера составляем так, чтобы в каждое входило усилие только в одном разрезанном стержне. Это достигается путём выбора в качестве моментных точек Риттера – точек, где пересекаются усилия в двух разрезанных стержнях (точки
направляем вначале от узлов, т.е. считаем, что стержни растянуты. Составляем три уравнения равновесия для плоской произвольной системы сил, действующих на выделенную часть. Уравнения равновесия в методе Риттера составляем так, чтобы в каждое входило усилие только в одном разрезанном стержне. Это достигается путём выбора в качестве моментных точек Риттера – точек, где пересекаются усилия в двух разрезанных стержнях (точки 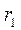 и
и 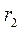 ), и соответствующего выбора осей, на которые проектируются силы
), и соответствующего выбора осей, на которые проектируются силы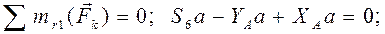
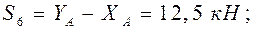
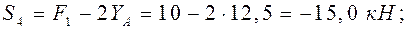
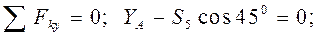

 Тело A (рис. 57) весом
Тело A (рис. 57) весом 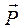 находится на шероховатой (реальной) поверхности. К телу с помощью нити, перекинутой через идеальный блок, подвешена чашка с разновесками, суммарный вес которых Q. Если Q мал, то тело А будет покоиться. Объясняется это тем, что на тело, кроме силы натяжения нити Q, веса
находится на шероховатой (реальной) поверхности. К телу с помощью нити, перекинутой через идеальный блок, подвешена чашка с разновесками, суммарный вес которых Q. Если Q мал, то тело А будет покоиться. Объясняется это тем, что на тело, кроме силы натяжения нити Q, веса 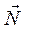 , в месте его контакта с поверхностью действует сила трения
, в месте его контакта с поверхностью действует сила трения 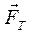 . Составим два уравнения равновесия для тела A:
. Составим два уравнения равновесия для тела A: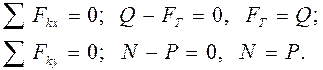
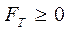 . Изучение равновесия тел при наличии трения скольжения базируется на законах Кулона - Амантона.
. Изучение равновесия тел при наличии трения скольжения базируется на законах Кулона - Амантона. , поэтому
, поэтому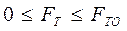 .
.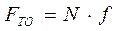 ,
, – безразмерный коэффициент пропорциональности, называемый коэффициентом трения скольжения.
– безразмерный коэффициент пропорциональности, называемый коэффициентом трения скольжения.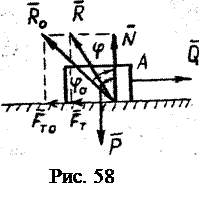 Тело A (рис. 58) находится на шероховатой поверхности. На тело действуют силы, указанные на рис. 57. Так как
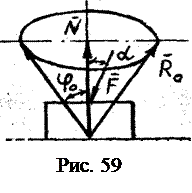
Тело A (рис. 58) находится на шероховатой поверхности. На тело действуют силы, указанные на рис. 57. Так как  есть полная реакция опорной поверхности, наклонённая к вертикали под углом
есть полная реакция опорной поверхности, наклонённая к вертикали под углом 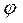 . Если сила трения приобретает свое предельное значение (что наблюдается при движении тела относительно опорной поверхности), т.е.
. Если сила трения приобретает свое предельное значение (что наблюдается при движении тела относительно опорной поверхности), т.е. 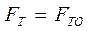 , то реакция поверхности
, то реакция поверхности  приобретает своё максимальное значение
приобретает своё максимальное значение  , равное
, равное 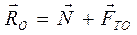 .
.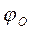 наклона максимальной реакции поверхности
наклона максимальной реакции поверхности 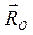 к вертикали называется углом трения. Из рис. 58 следует, что
к вертикали называется углом трения. Из рис. 58 следует, что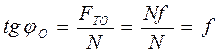 .
. Если описать максимальной реакцией поверхности
Если описать максимальной реакцией поверхности  .
.

 . Зная углы
. Зная углы 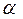 ,
, 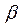 и угол трения
и угол трения  .
.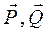 . Реакции связей:
. Реакции связей: 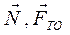 .
.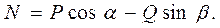
 . (3.2)
. (3.2)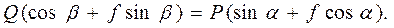 (3.3)
(3.3)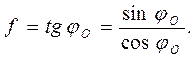 (3.4)
(3.4)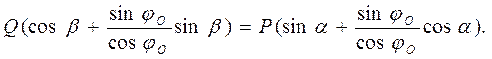

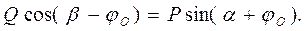 (3.5)
(3.5)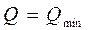 при
при  Значит,
Значит, 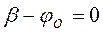 .
.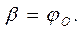
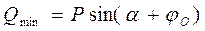 .
.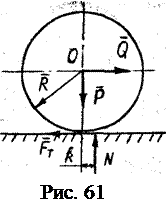 На каток радиусом R и весом P действует горизонтальная сила
На каток радиусом R и весом P действует горизонтальная сила  (рис. 61). В точке контакта катка с поверхностью возникают сила трения скольжения
(рис. 61). В точке контакта катка с поверхностью возникают сила трения скольжения 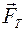 и нормальная реакция
и нормальная реакция 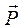 и
и 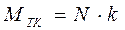 ,
,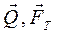 образуют пару, которая катит каток.
образуют пару, которая катит каток.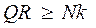 , откуда
, откуда  .
.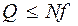 . Очевидно, справедливо неравенство
. Очевидно, справедливо неравенство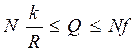 .
.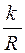 существенно меньше f.
существенно меньше f.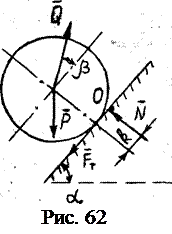 Какую силу Q (рис. 62) надо приложить к катку радиуса R и весом P, чтобы равномерно катить его по наклонной плоскости, если угол наклона плоскости к горизонтали – a, угол наклона силы
Какую силу Q (рис. 62) надо приложить к катку радиуса R и весом P, чтобы равномерно катить его по наклонной плоскости, если угол наклона плоскости к горизонтали – a, угол наклона силы  к плоскости –
к плоскости –  , коэффициент трения качения равен k.
, коэффициент трения качения равен k.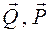 .
. , нормальная реакция поверхности
, нормальная реакция поверхности  .
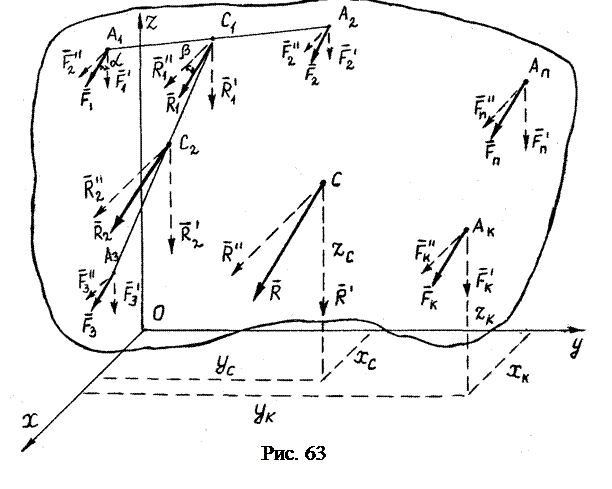
.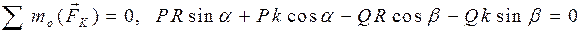 .
.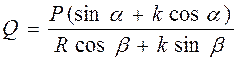 .
. На тело действует пространственная система параллельных сил
На тело действует пространственная система параллельных сил 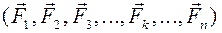 (рис. 63). Силы приложены в точках
(рис. 63). Силы приложены в точках  .
.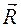 данной системы сил. Для этого сложим вначале силы
данной системы сил. Для этого сложим вначале силы  и
и 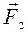 . Модуль равнодействующей системы параллельных сил равен их алгебраической сумме, значит
. Модуль равнодействующей системы параллельных сил равен их алгебраической сумме, значит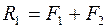 . (4.1)
. (4.1)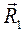 приложена в точке С 1, положение которой определим, воспользовавшись теоремой Вариньона о моменте равнодействующей относительно точки С 1:
приложена в точке С 1, положение которой определим, воспользовавшись теоремой Вариньона о моменте равнодействующей относительно точки С 1: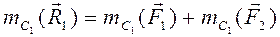 .
. , то получим
, то получим . (4.2)
. (4.2)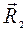 сил
сил 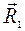 и
и 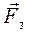
 . (4.3)
. (4.3)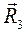 , получим:
, получим: . (4.4)
. (4.4)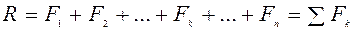 . (4.5)
. (4.5)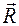 приложена в точке С, которая называется центром параллельных сил.
приложена в точке С, которая называется центром параллельных сил. , модуль равнодействующей
, модуль равнодействующей 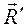 и положение точки С, в которой она приложена, не меняются, так как остаются справедливыми все выражения (4.1) – (4.5).
и положение точки С, в которой она приложена, не меняются, так как остаются справедливыми все выражения (4.1) – (4.5).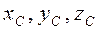 центра параллельных сил С и координаты
центра параллельных сил С и координаты  приложения силы
приложения силы 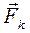 .
. относительно оси Oy:
относительно оси Oy: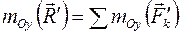 или
или 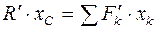 ,
, .
.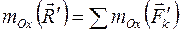 или
или 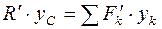 ,
,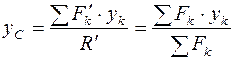 .
. центра параллельных сил воспользуемся основным свойством параллельных сил: поворачиваем (рис. 63) все силы системы на угол
центра параллельных сил воспользуемся основным свойством параллельных сил: поворачиваем (рис. 63) все силы системы на угол 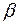 до их горизонтального положения. Получим систему сил
до их горизонтального положения. Получим систему сил 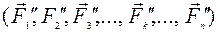 , параллельных оси Ox. Запишем для этой системы сил теорему Вариньона о моменте равнодействующей относительно оси Оу:
, параллельных оси Ox. Запишем для этой системы сил теорему Вариньона о моменте равнодействующей относительно оси Оу: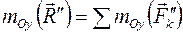 или
или 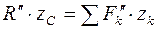 ,
, .
. ,
, 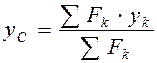 ,
,  . (4.6)
. (4.6)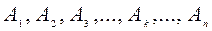 , вес которых соответственно равен
, вес которых соответственно равен  . Отсюда следует, что на тело действует система параллельных сил. Равнодействующая этой системы сил есть вес тела
. Отсюда следует, что на тело действует система параллельных сил. Равнодействующая этой системы сил есть вес тела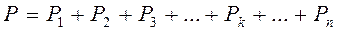 .
.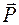 , называется центром тяжести тела.
, называется центром тяжести тела.
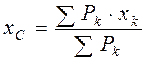 ,
, 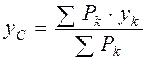 ,
,  . (4.7)
. (4.7)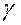 вес единицы объёма тела (удельный вес).
вес единицы объёма тела (удельный вес).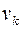 равен
равен  . Вес тела объёмом V равен
. Вес тела объёмом V равен .
.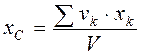 ,
, 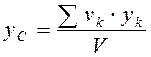 ,
, 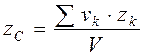 , (4.8)
, (4.8) – координаты центра тяжести k -го тела объёмом
– координаты центра тяжести k -го тела объёмом 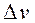 и, переходя в выражениях (4.8) к пределу при
и, переходя в выражениях (4.8) к пределу при  , получаем выражение (4.9):
, получаем выражение (4.9):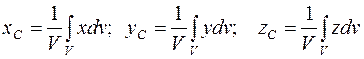 . (4.9)
. (4.9)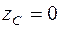 .
.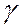 – вес единицы площади тела. Вес k -го элемента тела площадью
– вес единицы площади тела. Вес k -го элемента тела площадью 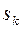 равен
равен  , вес тела площадью S равен
, вес тела площадью S равен .
.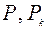 в выражения (4.7), получаем координаты центра тяжести однородного плоского тела:
в выражения (4.7), получаем координаты центра тяжести однородного плоского тела: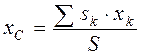 ,
, 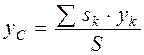 . (4.10)
. (4.10)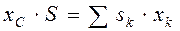 ,
, 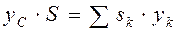 . (4.11)
. (4.11) . Из выражений (4.11) следует, что в этом случае статические моменты тела равны 0:
. Из выражений (4.11) следует, что в этом случае статические моменты тела равны 0: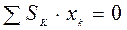 ,
, 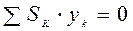 .
. . (4.12)
. (4.12)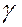 вес единицы длины тела. Тогда вес
вес единицы длины тела. Тогда вес  тела длиной lk равен
тела длиной lk равен 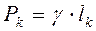 , вес тела длиной L равен
, вес тела длиной L равен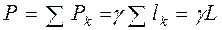 .
.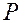 ,
,  в выражения (4.7), получаем после сокращения на
в выражения (4.7), получаем после сокращения на  координаты центров тяжести однородной линии:
координаты центров тяжести однородной линии: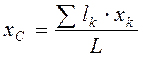 ,
, 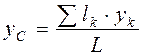 ,
, 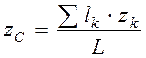 . (4.13)
. (4.13) . (4.14)
. (4.14) .
. Следовательно:
Следовательно: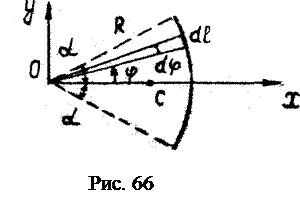 Центр тяжести однородной дуги радиусом R и центральным углом 2 a.
Центр тяжести однородной дуги радиусом R и центральным углом 2 a.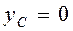 . Для определе-ния координаты
. Для определе-ния координаты  воспользуемся выражением из формулы (4.14)
воспользуемся выражением из формулы (4.14)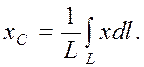 (4.16)
(4.16)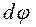 . Тогда
. Тогда и длина дуги
и длина дуги  .
. .
.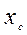 центра тяжести однородной дуги определяется выражением
центра тяжести однородной дуги определяется выражением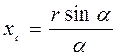 , (4.16)
, (4.16)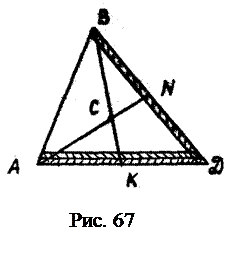 Разбивая треугольник на тонкие полоски параллельные стороне ВД, получим, что их центры тяжести лежат на медиане AN. Следовательно, центр тяжести треугольника C находится в точке пересечения его медиан.
Разбивая треугольник на тонкие полоски параллельные стороне ВД, получим, что их центры тяжести лежат на медиане AN. Следовательно, центр тяжести треугольника C находится в точке пересечения его медиан.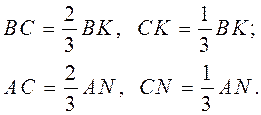
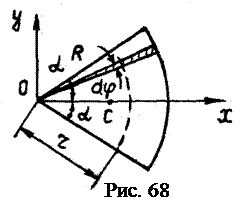 Сектор (рис. 68) симметричен относительно биссектрисы централь-ного угла, с которой совмещаема ось Ox. В этом случае координата
Сектор (рис. 68) симметричен относительно биссектрисы централь-ного угла, с которой совмещаема ось Ox. В этом случае координата 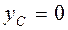 .
.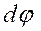 . Этот элементарный сектор можно считать треугольником, центр тяжести которого находится на расстоянии
. Этот элементарный сектор можно считать треугольником, центр тяжести которого находится на расстоянии 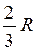 , поэтому центры тяжести элементарных секторов находятся на дуге
, поэтому центры тяжести элементарных секторов находятся на дуге  .
. . (4.17)
. (4.17) вырезана четвёртая часть круга 2 радиусом R и присоединён треугольник 3.
вырезана четвёртая часть круга 2 радиусом R и присоединён треугольник 3.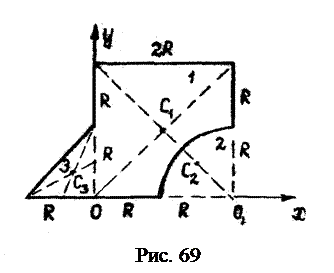 Разбиваем тело на три элемента. Определяем площадь и координаты центров тяжести каждого элемента.
Разбиваем тело на три элемента. Определяем площадь и координаты центров тяжести каждого элемента.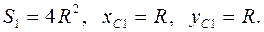

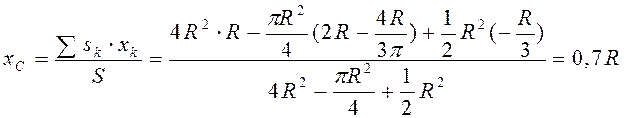 ;
; .
.


