Равновесие с учетом сил трения

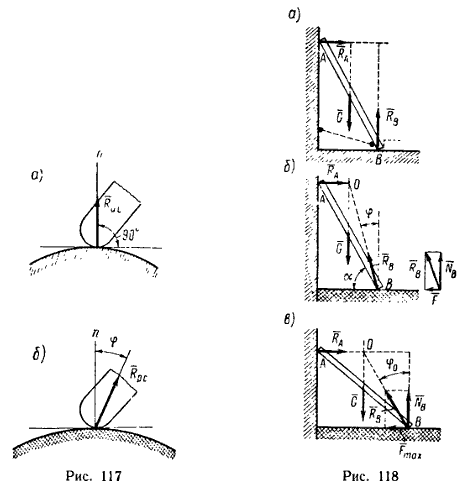
Задачи, приведенные в этом параграфе, отличаются от предыдущих тем, что в них рассматривается равновесие тел, имеющих, кроме идеальных, еще и реальные связи, т. е. связи с трением (Е. М. Никитин, § 34, 35 и 36).

При свободном опирании тела на поверхность идеальной связи реакция такой связи R_и.с.(рис. 117, а) направлена перпендикулярно к ее поверхности, т. е. по нормали n к этой поверхности.

Если же тело опирается на поверхность реальной связи (в отличие от идеальных связей реальные связи условимся отмечать двойной штриховкой), то ее реакция R_р.с. (рис. 117, б) в зависимости от нагрузок, приложенных к телу, отклонится от нормали n к поверхности связи на некоторый угол φ.

Поясним это общее положение следующим примером.

Наклонный брус (рис. 118, а), вес которого G, опирается в двух точках А и В соответственно на вертикальную и горизонтальную поверхности идеальных связей. Этот брус не может находиться в равновесии, потому что три силы – вес бруса G и реакции R_A и R_B – расположены так, что не выполняется необходимое условие равновесия трех непараллельных сил; их линии действия не пересекаются в одной точке.

Чтобы брус, показанный на рис. 118, а, находился в равновесии, необходимо наложить еще одну связь, например, удержать брус шнуром или упереть в выступ на горизонтальной плоскости (обе возможные связи показаны пунктиром).

Теперь представим, что в точке В брус опирается не на идеально гладкую, а на шероховатую (реальную) поверхность (рис 118, б). В этом случае брус может находиться в равновесии без дополнительной связи (шнура или упорной планки). Значит три силы – вес G и реакции опор R_A и R_B – образуют уравновешенную систему. Равновесие трех сил, действующих на брус, возможно потому, что реакция R_B реальной связи отклоняется на некоторый угол φ от нормали к поверхности связи и линии действия всех трех сил пересекаются в точке О.

Если реакцию R_B реальной связи разложим на две составляющие, направленные вдоль поверхности и перпендикулярно к ней (это разложение показано на рис. 118, а справа), то получим силу N_B – нормальную составляющую R_B, численно равную нормальному давлению, производимому концом бруса на опору, и силу F – касательную составляющую реакции R_B, которая называется силой трения.

При увеличении угла α, характеризующего наклон бруса относительно горизонтальной поверхности, угол φ уменьшается, а вместе с ним уменьшается и сила трения, но брус сохраняет равновесие.

Если же уменьшать угол α, то угол φ, характеризующий отклонение реакции R_B от нормали, увеличивается, а вместе с ним увеличивается и сила трения (рис. 118, в). При некотором наклоне бруса, определенном для данной пары соприкасающихся в точке В тел (например, для деревянного бруса, опирающегося о деревянный пол), брус скользит. Это означает, что сила трения, достигая предельного значения, больше увеличиваться не может. При этом реакция отклоняется также до предельного значения φ=φ₀ и при дальнейшем уменьшении угла α линия действия реакции R_B уже не попадает в точку пересечения сил G и R_A.

Угол φ₀, соответствующий F_max – максимальному значению силы трения, называется углом трения. Числовое значение угла трения зависит от материала соприкасающихся тел и от состояния их поверхностей.

Для случая предельного равновесия (грань между покоем и движением; § 36 в учебнике Е. М. Никитина) между силой трения и углом трения имеем такую зависимость:
F_max / N_B = tg φ₀.

Постоянное для данной пары соприкасающихся тел значение tg φ₀=f называется коэффициентом трения при покое. Таким образом,
F_max = fN.

При решении задач необходимо учитывать, что сила трения направлена всегда в сторону, противоположную той, при которой точка может скользить по идеальной поверхности.

Если в число реакций связей, обеспечивающих равновесие тела, входит сила трения, то такое состояние равновесия называется самоторможением (условие самоторможения тела в общей форме изложено в конце § 36 учебника Е. М. Никитина). Во всех приведенных ниже задачах рассмотрены различные случаи самоторможения (равновесия при наличии силы трения) и условия, при которых возможно самоторможение.

Задача 89. Тело А массой 8 кг поставлено на шероховатую горизонтальную поверхность стола. К телу привязана нить, перекинутая через блок Б (рис. 119,...

Задача 90. При каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую...

Задача 91. В месте соприкосновения пола и лестницы в предыдущей задаче коэффициент трения f=0,4. Сможет ли человек, масса которого 70 кг, подняться по лестнице...

Задача 92. При каких значениях угла α, образуемого с гладкой вертикальной стеной, лестница, опирающаяся нижним концом о шероховатый горизонтальный...

Задача 94. Цилиндр с горизонтальной площадкой наверху (рис. 123, а), находясь в двух кольцевых направляющих, скользит вниз, так как между поверхностью...

Задача 95. Тело А поставлено на негладкую пластину BC, которую можно поворачивать около шарнира В. Коэффициент трения f между телом А и пластиной BC известен...

Сочлененные системы

Сочлененной называется система нескольких тел, соединенных друг с другом при помощи внутренних связей: простого опирания, стержней или нитей (цепей), шарниров.

При решении некоторых задач с сочлененными системами равновесие каждого тела системы рассматривают отдельно. При этом в месте сочленения тел возникают две силы, одна из которых приложена к одному телу, а другая – ко второму телу. Эти силы равны по модулю, направлены вдоль одной прямой, но в противоположные стороны (закон равенства действия и противодействия).

На рис. 126 показаны силы взаимодействия, возникающие между телами А и В: P_AB – действие тела А на тело В и P_BA – действие тела В на тело А. Если, например, тело А служит опорой для В (связью), то P_AB – реакция связи, приложенная к телу B, а P_BA – сила давления (нагрузка), приложенная к телу А.

На рис. 127 показаны силы, возникающие при взаимодействии тел A и B не непосредственно друг с другом, а через стержень. Если допустить, что тело А действует на В через стержень силой T_AB, то тогда со стороны тела В возникнет сила T_BA. В задачах, как правило, рассматривают только эти две силы, приложенные к телам А и В (рис. 127, а).

На рис. 127, б показаны силы, приложенные только к стержню, т. е. показаны действия на стержень тел А и В.

Если два тела А и В связаны друг с другом при помощи так называемого внутреннего шарнира (рис. 128), то направление сил взаимодействия заранее неизвестно. Поэтому каждая из сил взаимодействия между телами (силы R_AB и R_BA – предположительно показаны на рис. 128 штриховыми векторами) заменяются составляющими X_AB, Y_AB и X_BA, Y_BA. Причем для этих векторов выполняются следующие равенства:
R_AB=-R_BA, X_AB=-X_BA и Y_AB=-Y_BA.

Задача 97. Балка АВ, имея в точке А шарнирное крепление, опирается в точке В на балку CD (рис. 129, а), которая удерживается в равновесии стержнем...

Задача 98. Балка АВ жестко заделана у точки А и нагружена по всей длине равномерно распределенной нагрузкой интенсивностью q=8 кн/м (рис. 130, а)...

При решении задач, в которых сочленение тел произведено при помощи промежуточного шарнира, целесообразно сначала составить уравнения равновесия для всей системы, а затем добавить к ним уравнение моментов сил относительно промежуточного шарнира для одного из тел сочлененной системы.

Покажем это на примере следующей задачи.

Задача 99. Балки 1 и 2 шарниром С соединенные между собой, шарнирно прикреплены к неподвижным опорам в точках А и В (рис. 131, а). Длина балок одинакова:...

Задача 100. На наклонных плоскостях АС и ВС помещены два тела 1 и 2, связанные нитью, которая перекинута через блок D (рис. 132, а), f₁ –...