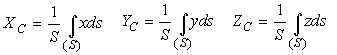Законы трения скольжения. Равновесие при наличии трения скольжения.

1) сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Величина силы трения зависит от активных сил и заключена между нулем и своим максимальным значением, которое достигается в момент выхода тела из положения равновесия (0 ≤ F_тр ≤ F_тр^max);

2) максимальное значение силы трения скольжения не зависит от площади контакта, а определяется величиной нормальной реакции, материалом и состоянием контактирующих поверхностей;

F_тр^max = fN,

где f – коэффициент трения скольжения, который является безразмерной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления.

Экспериментально установлено, что f < f_сц.

 

Конус трения – поверхность, образованная линией действия максимальной реакции опорной поверхности при движении тела в различных направлениях.

 

При равновесии тела на шероховатой поверхности под действием силы P (рисунок 2.3) можно составить два уравнения равновесия:

ΣF_{kx = 0}; Psinα - F_{тр = 0};

ΣF_{ky = 0}; -Pcosα + N = 0.

Следовательно,

Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину.

 

Никакая сила, лежащая внутри конуса трения, не может вывести тело из состояния равновесия.

 

Трение качения. Равновесие при наличии трения качения.

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого. Вследствие деформации тел их касание происходит вдоль площадки AB (рисунок а), появляется распределенная система сил реакции (рисунок б), которая может быть заменена силой и парой (рисунок в).

 

Сила раскладывается на две составляющие – нормальную и силу трения скольжения. Пара сил называется моментом сопротивления качению M_c.

 

При равновесии тела момент сопротивления качению определяется из условий равновесия системы сил. При этом установлено, что момент сопротивления принимает значения от нуля до максимального значения. Максимальное значение момента сопротивления, соответствующее началу качения, определяется равенством

M_c^max = Nδ,

где δ – коэффициент трения качения, имеет размерность длины [м], зависит от материала контактирующих тел и геометрии зоны контакта.

 

13. Определение первого и второго статических инвариантов. Частные случаи приведения произвольной системы сил к центру.

 

Теорема Вариньона в векторной и скалярной формах

Момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.

 

Например, момент силы F относительно точки O можно определить как алгебраическую сумму моментов сил F_x и F_y (на которые можно разложить силу F) относительно той же точки O. То есть

 

M_o(F)= -Fh = -F_x y+ F_y x,

 

где F_x, F_y, x и y – проекции на оси координат силы F и радиуса-вектора r.

 

Центр тяжести. Основные методы.

 

Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела

 

 

Радиус-вектор этой точки

 

Метод интегрирования.

Выражаем координаты центра тяжести неоднородного тела следующим образом:

Для однородных тел (центры тяжести объема, поверхности, площади и линии) эти координаты мы находим по формулам:

dv, ds, dl - элементарные объемы, площади и отрезки, x,y,z - координаты этих элементарных объемов, площадей и отрезков, а P для неоднородного тела вычисляется как

Метод симметрии.

 

 

Метод применяется только для однородных тел. Опуская несложные доказательства, сформулируем три правила метода.

1. Если тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.

2. Если тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

3. Если тело имеет центр симметрии, то центр тяжести тела находится в этой точке.

Используя правила, определим положение центра тяжести однородного цилиндра высотой H.

Рассечем цилиндр по диаметру плоскостью П₁, которая является первой плоскостью симметрии цилиндра (рис. 43). Рассекая цилиндр по другому диаметру второй плоскостью симметрии П₂, найдем ось симметрии AA цилиндра, являющуюся линией пересечения двух плоскостей симметрии и совпадающую с осью цилиндра. Наконец, рассекая цилиндр пополам плоскостью П₃, перпендикулярной оси цилиндра, найдем центр симметрии C, находящийся в точке пересечения плоскости симметрии П₃ с осью симметрии AA. Таким образом, центр тяжести однородного цилиндра находится на оси цилиндра на высоте H/2 от основания (рис. 43).

Метод разбиения.

Он применяется, когда однородное тело можно разбить на части, положения центров тяжести которых известны или легко определяются. В неоднородном теле эти части должны иметь еще и одинаковый удельный вес во всех их точках. После разбиения положение центра тяжести всего тела находят, используя дискретные формулы для определения координат центра тяжести.

Применим метод для плоского однородного треугольника. Разобьем треугольник ABD на узкие полоски, параллельные стороне AD (рис. 44). Центры тяжести отрезков линий, за которые в пределе приняты полоски, будут лежать на медиане BC₁, там же должен лежать и центр тяжести всего треугольника. Аналогичные результаты получатся для медианы DC₂, когда полоски параллельны стороне AB треугольника. Следовательно, точка C пересечения медиан будет центром тяжести всего треугольника. Причем из геометрии известно, что CC₁ = BC₁ / 3, а CC₂ = DC₂ / 3.