
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил системы на оси координат были равны нулю.Содержание книги
Поиск на нашем сайте
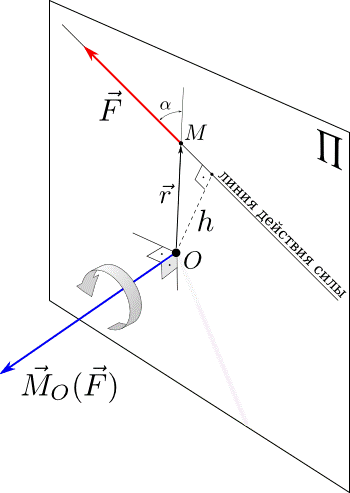
Момент силы относительно центра Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.
Если известен радиус-вектор r ⃗ точки приложения силы F ⃗ относительно точки О, то момент этой силы относительно О выражается следующим образом: M ⃗ O (F ⃗) = r ⃗× F ⃗.
| M ⃗ O | = | r ⃗× F ⃗| = | r ⃗|| F ⃗|sin α.
| M ⃗ O | = | F ⃗| h.
Момент силы относительно оси. Аналитический и геометрический способы. Проекция момента силы относительно точки на некоторую ось, проходящую через эту точку называется моментов силы относительно оси.
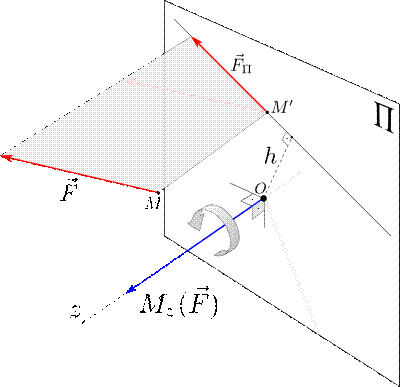
Момент силы относительно оси вычисляется как момент проекции силы F ⃗ на плоскость Π, перпендикулярную оси, относительно точки пересечения оси с плоскостью Π: Mz (F ⃗) = Mz (F ⃗Π) = ± F Π h. 1. Аналитический По правилу вычисления векторного произведения: Откуда 2. Геометрический
Для вычисления момента силы относительно оси необходимо провести плоскость Момент положителен, если, глядя с положительного направления оси, вращение видно происходящим против хода часовой стрелки.
Пара сил. Теорема о сумме моментов сил пары относительно произв. Центра. Пара сил - это система двух равных параллельных сил, направленных в разные стороны
Кратчайшее расстояние между линиями действия сил называют плечом пары h, а плоскость П, где лежит пара сил, является плоскостью пары.
Первое свойство. Пару сил нельзя привести к силе. Второе свойство. Действие пары сил на твердое тело определяется моментом пары, который является свободным вектором, перпендикулярным плоскости пары, численно равным произведению силы на плечо пары. Следствия из второго свойства пары. 1. Действие пары на твердое тело не изменяется, если пару сил поворачивают в плоскости пары. 2. Действие пары сил на твердое тело не изменяется, если пару сил переносят в другое место плоскости пары. 3. Действие пары сил на твердое тело не изменяется, если ее перенести в плоскость, параллельную плоскости пары. Сумма моментов сил пары относительно произвольной точки равна моменту пары. Доказательство. Выберем произвольную точку так как Следствие: Момент пары не зависит от выбора центра.
Теоремы о парах.
Теорема 1. Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. Для док–ва рассмотрим две пары (F1, F`1) и (F2, F`2) (рис. 3.9) и перенесем точки приложения всех сил вдоль линий их действия в точки А и В соответственно. Складывая силы по аксиоме 3, получим R=F1+F2 и R'=F`1+F`2, но F'1=–F1 и F`2=–F2. Следовательно, R=–R', т. е. силы R и R' образуют пару. Момент этой пары: М=М(R, R')=ВАxR=BAx(F1+F2)=ВАxF1+ВАxF2. (3.14). При переносе сил, составляющих пару, вдоль линий их действия ни плечо, ни направление вращения пары не меняются, следовательно, не меняется и момент пары. Значит, ВАхF1=M(F1, F'1)=M1, ВАxF2=M(F2, f`2)=M2, и формула (З.14) примет вид M=M1+M2, (3.15) ч.т.д. Сделаем два замечания. 1. Линии действия сил, составляющих пары, могут оказаться параллельными. Теорема остается справедливой и в этом случае. 2. После сложения может получиться, что М(R,R')=0; на основании замечания1 из этого следует, что совокупность двух пар (F1, F`1, F2, F`2)~0.
Теорема 2. Две пары, имеющие равные моменты, эквивалентны. Пусть на тело в плоскости I действует пара (F1,F`1) с моментом M1. Покажем, что эту пару можно заменить другой парой (F2, F`2), расположенной в плоскости II, если только ее момент М2 равен М1. Заметим, что плоскости I и II должны быть параллельны, в частности, они могут совпадать. Действительно, из параллельности моментов M1, и М2 следует, что плоскости действия пар, перпендикулярные моментам, также параллельны. Введем в рассмотрение новую пару (F3, F`3) и приложим ее вместе с парой (F2, F`2) к телу, расположив обе пары в плоскости II. Для этого согласно аксиоме 2 нужно подобрать пару (F3, F`3) с моментом М3 так, чтобы приложенная система сил (F2, F`2, F3, F`3) была уравновешена. Положим F3=–F`1 и F`3=–F1 и совместим точки приложения этих сил с проекциями А1 и B1 точек А и В на плоскость II (см. рис. 3.10). В соответствии с построением будем иметь: М3=–M1 или, учитывая, что М1=М2, М2+М3 = 0, получим (F2, F`2, F3, F`3)~0. Т.о., пары (F2, F`2) и (F3, F`3) взаимно уравновешены и присоединение их к телу не нарушает его состояния (аксиома 2), так что (F1, F`1)~(F1, F`1, F2, F`2, F3, F`3). (3.16). С другой стороны, силы F1 и F3, а также F`1 и F`3 можно сложить по правилу сложения параллельных сил, направленных в одну сторону. Они равны по модулю, поэтому их равнодействующие R и R' должны быть приложены в точке пересечения диагоналей прямоугольника ABB1A1, кроме того, они равны по модулю и направлены в противоположные стороны. Это означает, что они составляют систему, эквивалентную нулю. Итак, (F1, F`1, F3, F`3)~(R, R')~0. Теперь можем записать (F1, F`1, F2, F`2, F3,F`3)~(F2, F`2).(3.17). Сравнивая соотношения (3.16) и (3.17), получим (F1, F`1)~(F2, F`2), ч.т.д. Из этой теоремы следует, что пару сил можно перемещать и поворачивать в плоскости ее действия, переносить в параллельную плоскость; в паре можно менять одновременно силы и плечо, сохраняя лишь направление вращения пары и модуль ее момента (F1h1=F2h2).
Теорема 3. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен сумме моментов двух данных пар. Пусть пары (F1, F`1) и (F2, F`2) расположены в пересекающихся плоскостях I и II соответственно. Пользуясь следствием теоремы 2, приведем обе пары к плечу АВ (рис. 3.11), расположенному на линии пересечения плоскостей I и II. Обозначим трансформированные пары через (Q1, Q`1) и (Q2, Q`2). При этом должны выполняться равенства: M1=M(Q1, Q`1)=M(F1, F`1) и M2=M(Q2, Q`2)=M(F2, F`2). Сложим по аксиоме 3 силы, приложенные в точках А и В соответственно. Тогда получим R=Q1+Q2 и R'=Q`1+Q`2. Учитывая, что Q`1=–Q1 и Q`2= –Q2, получим: R=–R'. Т.о., мы доказали, что система двух пар эквивалентна одной паре (R, R'). Найдем момент М этой пары. М(R, R')=ВАxR, но R=Q1+Q2 и М(R, R')=ВАх(Q1+Q2)=BAxQ1+BAxQ2=M(Q1, Q`1)+M(Q2, Q`2)=M(F1, F'1)+M(F2, F`2), или M=M1+M2, т. е. теорема доказана. Вывод: момент пары является свободным вектором и полностью определяет действие пары на абсолютно твердое тело. Для деформируемых тел теория пар неприменима.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.247.58 (0.009 с.) |

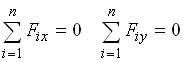
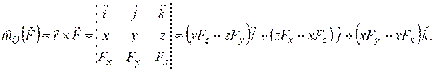
 ,
, ,
, .
.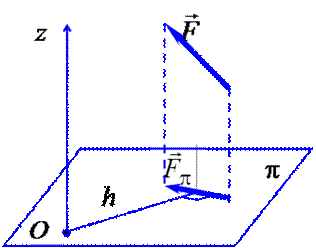
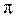 (рис. 3.4), перпендикулярную данной оси
(рис. 3.4), перпендикулярную данной оси  , спроецировать силу на эту плоскость и вычислить момент проекции
, спроецировать силу на эту плоскость и вычислить момент проекции 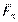 относительно точки
относительно точки 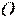 − точки пересечения оси
− точки пересечения оси 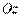 с плоскостью
с плоскостью  . Эквивалентность этих двух способов вытекает из равенств
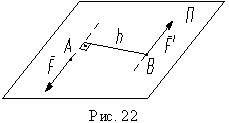
. Эквивалентность этих двух способов вытекает из равенств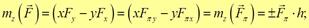 .
.
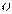 (рис. 3.7). Сумма моментов сил пары относительно точки
(рис. 3.7). Сумма моментов сил пары относительно точки 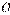 :
: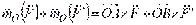 ,
, , то
, то 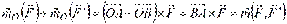 .
.





