
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Т.М. 1. Условия равновесия плоской системы сил. Виды связей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Т.М. 4. Расчет ферм. Сущность метода Риттера. Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция. Если оси стержней лежат в одной плоскости, то ее называют плоской фермой. Точки, в которых сходятся оси стержней, называются узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс, а расположенные по нижнему контуру – нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные – раскосами. На рисунке изображены стержневые опоры фермы.
Реакция каждого из опорных стержней, очевидно, направлена по оси этого стержня. Если шарниры, соединяющие стержни фермы, предполагаются идеальными, т.е. без трения, а все внешние силы - приложенными к узлам фермы, то все стержни испытывают лишь растяжение или сжатие, так как к каждому стержню приложены силы только на его концах. Реальные фермы не имеют идеальных шарниров, однако такое допущение облегчает вычисление усилий в стержнях фермы, а результаты вычислений при этом допущении вполне пригодны для практики. Применим метод сечений к определению усилий в стержнях плоских ферм. Рассмотрим ферму изображенную на рисунке.
На ферму действуют вертикальные внешние силы: задаваемая сила При определении усилий все стержни фермы условимся считать растянутыми, знак минус в ответе будет означать, что стержень сжат. Пусть требуется определить усилие в стержне 6 фермы. Для этого проводим сечение 1-1, рассекая не более трех стержней, в том числе стержень 6, усилие в котором определяется. Мысленно отбрасываем левую часть фермы, заменяя ее действие на оставшуюся правую часть усилиями Чтобы определить усилие
Так как Воспользуемся тем же сечением 1-1 для определения усилия
Для определения усилия
Знаки полученных ответов показывают, что стержень 6 растянут, а стержни 7 и 8 сжаты. Изложенный способ определения усилий в стержнях фермы предложен Риттером и носит название способа Риттера (использована система уравнений равновесия плоской системы сил).
Т.М. 11. 4 закона динамики. Первый закон динамики (закон инерции): Материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока действие каких-либо сил не выведет ее из этого состояния. Равномерное и прямолинейное движение точки называют движением инерции. Покой является частным случаем движения по инерции, когда скорость точки равна нулю. Всякая материальная точка обладает инертностью, т.е. стремиться сохранить состояние покоя или равномерного прямолинейного движения. Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной, а движение, наблюдаемое по отношению к этой системе, называется абсолютным. Любая система отсчета, совершающая относительно инерциальной системы поступательное прямолинейное и равномерное движение, будет также инерциальной системой. Второй закон (основной закон динамики): Ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и совпадает с силой по направлению: Из основного закона динамики следует, что при силе Третий закон (закон действия и противодействия): Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены вдоль одной прямой в противоположны е стороны. Силы, именуемые действием и противодействием, приложены к разным телам и поэтому уравновешенной системы сил не образуют. Четвертый закон динамики (закон зависимости действия сил): При одновременном действия нескольких сил ускорение материальной точки равно геометрической сумме ускорений, которые имела бы точка при действии каждой силы в отдельности:
Т.М. 14. Теорема Штейнера.
Т.М. 1. Условия равновесия плоской системы сил. Виды связей. Аналитически условия равновесия тела под действием плоской системы сходящих сил определяются двумя уравнениями:
1. Произвольная пространственная система сил 2. Пространственная система параллельных сил 3. Пространственная система сходящихся сил 4. Произвольная плоская система сил 5. Плоская система параллельных сил 6. Плоская система сходящихся сил
Условия, определяющие свободу движения твердого тела, называются связями. Сила, заменяющая действие связи, называется реакцией связи. Реакции связей – силы пассивные. Задеваемые силы, приложенные к твердому телу, называются активными. Связи реализуются в виде каких-то тел, не входящих в изучаемую механическую систему, рассмотрим основные типы связей и их реакции. · Гладкая опорная поверхность. Для гладкой опорной поверхности реакции направлена по нормали к опорной поверхности соприкасающихся тел в точке их касания и приложена в этой точке. Если соприкасающиеся поверхности криволинейные, реакция связи проходит по общему перпендикуляру, проведенному через точку касания (рис. Б). Если касание происходит в точке, реакция связи направлена по нормали к поверхности тела (рис. В). На рис. А показаны реакции гладкой горизонтальной поверхности, без учета силы трения.
· Гибкая нерастяжимая нить (трос, канат, цепь) препятствует удалению тела
· Невесомый стержень. Стержень можно считать невесомым, если его собственный вес мал по сравнению с нагрузками, которые он воспринимает. Усилие. а следовательно, и реакция стержня направлены вдоль оси, проходящей через узловые точки, которыми стержень крепится к конструкции. · Шарнирное соединение тел. Цилиндрическим шарниром называется соединение двух тел посредством пальца (болта), проходящего через отверстия в этих телах. Шарнирное соединение позволяет телу только вращаться вокруг оси шарнира, перпендикулярной плоскости рисунка. Реакция шарнира должна быть направлена по общему перпендикуляру к соприкасающимся криволинейным поверхностям. Вследствие разности размеров втулки и пальца положения точки касания не определено, поэтому направление реакции цилиндрического шарнира заранее неизвестно. Реакцию раскладывают на две составляющие
· Шарнирно-подвижная опора допускает поворот вокруг оси шарнира и линейное перемещение на небольшое расстояние вдоль опорной поверхности. Реакция такой опоры направлена перпендикулярно опорной поверхности (рис.а, б, в).
· Подпятник и сферический шарнир закрепляют какую-либо точку тела так, что она не может совершить никаких перемещений в пространстве. Подпятники можно рассматривать как совокупность цилиндрического шарнира и опорной поверхности, поэтому реакция связи · Жесткая заделка (защемление) не допускает линейных перемещений, ни поворота, для такой опоры не известны не только величина и направление реакции, но и точка ее приложения. Для определения опорной реакции необходимо найти три неизвестные: составляющие
|
|||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 588; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.115 (0.011 с.) |



 и реакции опор
и реакции опор  .
. , приложенными в соответствующих сечениях стержней и направленными в сторону отброшенной части.
, приложенными в соответствующих сечениях стержней и направленными в сторону отброшенной части. независимо от усилий
независимо от усилий  , составляем уравнение моментов сил, действующих на правую часть фермы, относительно точки К, в которой пересекаются линии действия сил
, составляем уравнение моментов сил, действующих на правую часть фермы, относительно точки К, в которой пересекаются линии действия сил 
 , то
, то  .
.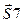 независимо от усилий
независимо от усилий  . Спроецируем все силы, действующие на правую часть фермы, на вертикальную ось y, так как проекции сил
. Спроецируем все силы, действующие на правую часть фермы, на вертикальную ось y, так как проекции сил  на эту ось равны нулю:
на эту ось равны нулю:
 составим уравнение моментов этих же сил относительно точки Риттера L, в которой пересекаются линии действия сил
составим уравнение моментов этих же сил относительно точки Риттера L, в которой пересекаются линии действия сил  :
:
 .
. ускорение
ускорение 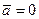 . Масса точки характеризует степень сопротивляемости точки изменению ее скорости, т.е. является мерой инертности материальной точки.
. Масса точки характеризует степень сопротивляемости точки изменению ее скорости, т.е. является мерой инертности материальной точки. .
.








 от точки подвеса. Реакция натянутой нити направлена вдоль нити к точке подвеса. Сила
от точки подвеса. Реакция натянутой нити направлена вдоль нити к точке подвеса. Сила  , с которой груз
, с которой груз  (рис. Б) растягивает нить, называется натяжением нити.
(рис. Б) растягивает нить, называется натяжением нити.

 , лежащие в плоскости, перпендикулярной оси шарнира. В строительстве и машиностроении в конструкциях зданий, мостов, машин, станков, транспортных средств широко используются балочные системы. Материалом для изготовления балок служит металл, железобетон, дерево. Балки воспринимают нагрузки. Поперечные относительно их осей. Опорные устройства балок предназначены для передачи усилий и соединения частей конструкции. Шарнирно-неподвижная опора допускает поворот балки вокруг оси шарнира. Но не допускает никаких линейных перемещений. Опорная реакция приложена в центре шарнира, раскладывается на составляющие
, лежащие в плоскости, перпендикулярной оси шарнира. В строительстве и машиностроении в конструкциях зданий, мостов, машин, станков, транспортных средств широко используются балочные системы. Материалом для изготовления балок служит металл, железобетон, дерево. Балки воспринимают нагрузки. Поперечные относительно их осей. Опорные устройства балок предназначены для передачи усилий и соединения частей конструкции. Шарнирно-неподвижная опора допускает поворот балки вокруг оси шарнира. Но не допускает никаких линейных перемещений. Опорная реакция приложена в центре шарнира, раскладывается на составляющие

 для такой опоры раскладывают на три составляющие:
для такой опоры раскладывают на три составляющие:  .
. опорной реакции по осям координат и реактивный момент
опорной реакции по осям координат и реактивный момент  относительно центра тяжести опорного сечения. Второй конец балки всегда свободный, поэтому балку называют консольной.
относительно центра тяжести опорного сечения. Второй конец балки всегда свободный, поэтому балку называют консольной.


