
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение устойчивости системы. Теоремы Лапласа, критерии устойчивостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исследование устойчивости САУ имеет огромное значение, так как САУ в замкнутом виде обычно склонны к неустойчивой работе. Устойчивость линейной системы определяется ее параметрами и не зависит от внешних воздействий. Процессы в САУ описываются неоднородным дифференциальным уравнением, общее решение которого состоит из двух составляющих: xвых(t) = xвых(вын)(t) + xвых(св)(t). Общее решение однородного дифференциального уравнения определяется корнями соответствующего характеристического уравнения, т.е. полюсами передаточной функции замкнутой системы. Общее решение однородного дифференциального уравнения равно:
где pi – корень характеристического уравнения (полюс системы), Если полюс pi вещественный и отрицательный, т.е. pi < 0, то соответствующее ему слагаемое в выражении (3.5) с ростом времени стремится к нулю. Если же pi – вещественный положительный полюс, т.е. pi > 0, то это слагаемое, а значит и вся свободная составяляющая, неограниченно возрастает. Паре комплексно-сопряженных полюсов pi,i+1 = αi + jβi, в свободной составляющей соответствует слагаемое:
где
Такое слагаемое стремится к нулю, если вещественные части комплексно-сопряженных полюсов отрицательны, в противном случае амплитуда колебаний соответствующего слагаемого в свободной составляющей непрерывно возрастает. Паре мнимых полюсов pi,i+1 = + jβi в выражении соответствует слагаемое: Ai sin(βit + определяющее незатухающие колебания с постоянной амплитудой Ai.
Таким образом, для устойчивости системы САР необходимо и достаточно, чтобы все корни характеристического уравнения на плоскости комплексного переменного Если корни характеристического уравнения находятся в левой полуплоскости Определение устойчивости САУ по полюсам ее передаточной функции называют прямым методом оценки устойчивости. Однако для оценки устойчивости линейной системы не обязательно вычислять значения ее полюсов, т.е. решать алгебраическое уравнение n-го порядка. Достаточно знать, все ли полюса находятся в левой полуплоскости комплексной плоскости р (являются «левыми»). Такой подход к определению устойчивости системы характерен для косвенных методов оценки устойчивости (критериев устойчивости), позволяющих судить о расположении полюсов на плоскости комплексного переменного Различают алгебраические и частотные критерии устойчивости. Отличие критериев друг от друга связано с использованием различных характеристик САУ, но при этом все они предполагают необходимость проверки необходимого и достаточного условия устойчивости.
Независимо от выбранного критерия устойчивости первоначально проверяется выполнение необходимого условия устойчивости, согласно которому все коэффициенты характеристического уравнения должны быть положительными, т.е. ai > 0 при i = 1,…,n. Если необходимое условие не выполняется, делается заключение о том, что система неустойчива. В противном случае необходимо переходить к проверке достаточного условия устойчивости, формулировка которого зависит от выбранного критерия устойчивости. В дальнейшем будем полагать, что необходимое условие устойчивости выполняется. Для систем первого и второго порядка необходимое условие устойчивости является достаточным. 6.1 Алгебраический критерий устойчивости Гурвица. Для оценки устойчивости линейной системы по критерию Гурвица необходимо из коэффициентов характеристического уравнения составить определитель Гурвица, размерность которого равна порядку системы. Определитель Гурвица имеет вид:
Порядок составления определителя Гурвица следующий. В качестве элемента первого столбца первой строки определителя записывается коэффициент an-1, а затем на главной диагонали располагаются коэффициенты характеристического уравнения с последовательно убывающими индексами. При этом в послед выражении нем столбце последней строки определителя записывается коэффициент Затем, начиная от коэффициентов, стоящих на главной диагонали, заполняются столбцы определителя так, чтобы индексы коэффициентов, расположенных над коэффициентами главной диагонали, последовательно убывали, а коэффициентов, расположенных под диагональными коэффициентами, – последовательно возрастали. Если в процессе заполнения столбца определителя индекс коэффициента достигает значения n или 0, то дальнейшее заполнение столбца осуществляется нулями. Далее необходимо вычислить значение определителя Гурвица и всех его диагональных миноров, которые получают из определителя путем отчеркивания равного числа строк и столбцов в левом верхнем углу определителя. Например, диагональный минор первого порядка равен Δ1 = an-1; диагональный минор второго порядка: Δ2 = а диагональный минор третьего порядка: Δ3 = Очевидно, что диагональный минор n-го порядка совпадает с определителем Гурвица. Линейная система устойчива, если при выполнении необходимого условия, определитель Гурвица и все его диагональные миноры будут положительны: Δ1 > 0, Δ2 > 0, …………,Δn > 0. Раскрыв определитель Гурвица по последнему столбцу, получим
Так как, в соответствие с необходимым критерием устойчивости
Если определитель Δn = 0, то САУ находится на границе устойчивости. При этом возможны два случая: 1) свободный член характеристического уравнения равен нулю, т.е. a0 = 0, что соответствует нейтрально устойчивой системе; 2) диагональный минор Δ(n-1) = 0, что соответствует колебательной границе устойчивости. Из условия Δ(n-1) = 0 можно определить параметры, при которых САУ находится на границе устойчивости.
6.2 Критерий устойчивости Михайлова Годограф характеристического вектора, т.е. кривую, которую описывает характеристический вектор при изменении частоты от 0 до ∞, называют кривой Михайлова. При аn > 0 кривая Михайлова начинается в положительной вещественной полуоси.
Из формулировки критерия следует, что система устойчива, если годограф Михайлова, начавшись на действительной оси при ω = 0, несколько раз последовательно пересекает действительную и мнимую ось. Значения ω, при которых происходят эти пересечения, являются корнями уравнения Y(ω) = 0 (при пересечении с действительной осью) и уравнения Х(ω) = 0 (при пересечении с мнимой осью). Следовательно, оценить устойчивость системы можно и без построения годографа: достаточно, чтобы корни указанных уравнений чередовались друг с другом.
6.3 Критерий Найквиста На практике более широкое применение, по сравнению с критерием Михайлова, нашел частотный критерий Найквиста, который позволяет судить об устойчивости замкнутой системы по частотным характеристикам этой системы в разомкнутом состоянии. 1 формулировка критерия Найквиста: система, устойчивая в разомкнутом состояние, будет устойчива и в замкнутом состоянии, если годограф амплитудно-фазовой характеристики разомкнутой системы не охватывает точку с координатами (-1, j0). В том случае, когда годограф частотной характеристики охватывает эту точку, система неустойчива. 2 формулировка критерия Найквиста: система, неустойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если годограф амплитудно-фазовой характеристики разомкнутой системы пересекает реальную ось на отрезке от -∞ до (-1, j0), причем число положительных переходов должно отличаться от числа отрицательных переходов на Для оценки устойчивости астатических систем годограф W(jω) дополняют дугой бесконечного радиуса, начинающейся на положительной действительной полуоси и проводимой до пересечения с годографом W(jω). Формулировка критерия устойчивости при этом не изменяется. Если годограф W(jω) разомкнутой системы проходят через точку (1, j0), то система в замкнутом состоянии находится на границе устойчивости.
6.4 Оценка устойчивости по логарифмическим характеристикам Оценку устойчивости замкнутой САУ можно осуществлять по логарифмическим амлитудно- и фазо-частотным характеристикам системы в разомкнутом состоянии: L(ω) и φ(ω). В том случае, когда годограф W(jω) не имеет точек пересечения с вещественной осью слева от точки с координатами (-1, j0), для устойчивости замкнутой системы необходимо и достаточно, чтобы выполнялось условие ωс < ωкр. По L(ω) и φ(ω) разомкнутой системы можно определить запасы устойчивости: запас по фазе Δφ отсчитывают по фазо-частотной характеристике на частоте среза ωс, а запас устойчивости по усилению ΔL равен значению ЛАХ на критической частоте ωкр, взятому с обратным знаком, т.е. ΔL = | L(ωкр)|. Если ωс = ωкр, то система находится на границе устойчивости. 6.5 Устойчивость систем с запаздыванием Рассмотрим устойчивость САУ, в состав которых входят звенья чистого запаздывания. Передаточную функцию разомкнутой системы с запаздыванием запишем в виде W(p) = Wбз(p)∙e-τp, где Wбз(p) – передаточная функция разомкнутой системы без запаздывания; τ – время запаздывания. Передаточной функции звена с запаздыванием соответствуют следующие амплитудно- и фазо-частотные характеристики разомкнутой системы: │W(p)│ = │Wбз(p)│; L(ω)= Lбз(ω); φ(ω) = φбз(ω) – ωτ, где Lбз(ω), φбз(ω) – соответственно логарифмические амплитудно- и фазо-частотная характеристики разомкнутой системы без запаздывания. Из этих характеристик следует, что запаздывание влияет только на фазо-частотную характеристику, создавая дополнительный отрицательный фазовый сдвиг. Поэтому устойчивые САУ, не содержащие звеньев чистого запаздывания, могут становиться неустойчивыми при включении в их состав таких звеньев.
Показатели качества системы
Для сравнительного анализа различных систем управления необходимо иметь некоторые числовые характеристики этих систем, позволяющие оценивать какая из них будет более эффективной. Эти числовые характеристики и называются критериями качества. Система управления характеризуется различными показателями, к которым в первую очередь можно отнести: точность, устойчивость, быстродействие надежность, стоимость, оптимальность и др. Учитывая большое разнообразие систем и объектов управления, в настоящее время разработано большое число различных критериев так или иначе включающих в себя вышеприведенные показатели. Между этими показателями (критериями качества) существует тесная взаимосвязь, поэтому стремление улучшить какой-либо показатель системы управления приводит к ухудшению другого. Так, например, стремление уменьшить ошибку регулирования приводит к уменьшению запаса устойчивости и быстродействия и наоборот, или повышение надежности системы неизбежно приводит к увеличению ее стоимости. Учитывая взаимосвязь между различными показателями систем управления задачу выбора или проектирования оптимальной системы можно рассматривать как задачу на условный экстремум. Найти экстремум (минимум и максимум) какого-либо показателя, например стоимости, при условии, что остальные показатели не превышают заранее заданной величины. Такой постановке отвечают интегральные критерии качества, представляющие собой определенные интегралы от некоторых функций переменных системы. Классификация показателей качества.
Наиболее полной характеристикой качества системы управления является ошибка e(t) =g(t)-y(t). Ошибка e(t), являясь функцией от времени, не очень удобна для оценки качества систем управления. Поэтому на практике при оценке качества чаще используют числовые показатели, которые прямо или косвенно характеризуют точность воспроизведения заданного движения. Ошибка e(t) зависит как от свойства системы управления (т. е. от уравнения), так и от внешнего воздействия. По этой причине показатели качества как характеристики свойства системы определяют при определенных внешних воздействиях, называемых типовыми. При оценке качества в переходном режиме в качестве типового воздействия используют ступенчатую функцию, а при оценке качества в установившемся режиме — полиномы времени t: At, At2,...
Прямыми показателями качества называются показатели, которые получаются непосредственно по переходной характеристике. Из прямых показателей качества наиболее часто используют время регулирования и перерегулирование.
Основные прямые показатели качества системы: - hуст - установившееся значение – конечное значение переходной характеристики; - tн - время нарастания – время до момента, когда переходная характеристика впервые достигает значения hуст; - перерегулирование - - время регулирования tр – время, за которое переходный процесс заканчивается (с заданной точностью - число колебаний n – число колебаний переходной характеристики за время tр. Первый выброс не учитывается; - частота колебаний -
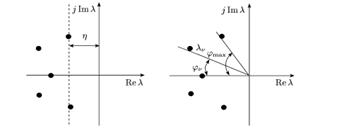
Корневые показатели качества. В качестве корневых показателей используют степень устойчивости и колебательность (степень колебательности). Степенью устойчивости системы управления (или характеристического полинома) называют расстояние от мнимой оси до ближайшего корня ее характеристического уравнения.
Степень колебательности, называемая также колебательностью, косвенно характеризует колебательность системы. Если степень колебательности равна нулю, то переходный процесс будет апериодическим. В общем случае можно ожидать, что при одинаковой степени устойчивости число колебаний за время регулирования будет больше у той системы, у которой больше степень колебательности.
По корневым показателям качества системы можно оценить значения основных прямых показателей качества:
Таким образом, степень устойчивости системы является косвенной мерой быстродействия системы. Степень колебательности, в свою очередь, является косвенной мерой устойчивости системы, причем чем величина степень колебательности меньше, тем больше запас устойчивости системы.
Частотные показатели качества. В качестве частотных показателей качества используют резонансный пик, полосу пропускания, запас устойчивости по фазе и запас устойчивости по амплитуде.
- M – частотный показатель колебательности, определяется по формуле:
- - - Показатель колебательности М характеризует запас устойчивости системы, чем выше показатель колебательности, тем меньше запас устойчивости. Допустимое значение М выбирается из условия М < 1,1-1,5. Величина частоты среза косвенной характеризует быстродействие системы:
при Помимо перечисленных частотных показателей качества, особое место занимают запасы устойчивости системы, которые определяются по АФХ разомкнутой системы или по ЛЧХ разомкнутой системы.
Запас устойчивости по амплитуде:
Запас устойчивости по фазе:
По логарифмическим характеристикам запас по фазе определяется по такому же соотношению, что и для определения запаса по АФХ, а для определения запаса по амплитуде используется следующая зависимость:
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.145.219 (0.008 с.) |

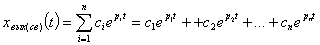 ,
,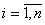 ; Ci – постоянная интегрирования.
; Ci – постоянная интегрирования. ,
, определяются через
определяются через  и
и 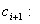
 .
.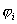 ),
), были расположены слева от мнимой оси. Только при этом все слагаемые в выражении будут стремиться к нулю.
были расположены слева от мнимой оси. Только при этом все слагаемые в выражении будут стремиться к нулю. .
.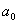 .
.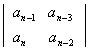 ,
, .
.
 > 0, то для проверки устойчивости системы достаточно уточнить знаки диагональных миноров с номерами от второго до
> 0, то для проверки устойчивости системы достаточно уточнить знаки диагональных миноров с номерами от второго до  .
.


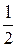 раз, где
раз, где  - число правых корней в характеристическом уравнении разомкнутой системы.
- число правых корней в характеристическом уравнении разомкнутой системы.

 ;
; ).
).  ;
; .
.
 .
. .
.



 ;
; - резонансная частота, частота, при которой АЧХ достигает максимальное значение;
- резонансная частота, частота, при которой АЧХ достигает максимальное значение; - граничная частота полосы пропускания системы;
- граничная частота полосы пропускания системы;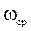 - частота среза, частота при которой
- частота среза, частота при которой  и затем АЧХ только убывает.
и затем АЧХ только убывает. ,
,


 , где а – расстояние от начала координат до точки пересечения АФХ отрицательной вещественной полуоси, т.е.
, где а – расстояние от начала координат до точки пересечения АФХ отрицательной вещественной полуоси, т.е.  .
. .
. .
.



