
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ческое напряжение. тем ниже устойчивость двигателей.Содержание книги
Поиск на нашем сайте CorJJacнo (12.42) залас устойчивости зависнт от загрузки део1га телей т. их электрнческ:ой удаленности Хш1 от шин 11еизменного В спучае бопьших внешних сопротивлений необходимо перей Напряжение в точке ВКJ]ючения нагрузIШ не явпяется неза- nиснмоl\ переменной, так как оно олредеJJяется режимом работы; yЗJia нагрузки:
Uдв=V0 V(x s•+l.)t((x.и +x,)'s'+r) (12.44;, В данном случае критические значения локазателей лредепь ноrо режима нельзя рассчитывать с учетом напряжения, опре деляеыоrо по (12.44). Они моrут быть найдены только оо напряже нию в системе Ис• которое ло условию от изменений режима не за-· висит. При постоя11ной потребляемой активности мощности (Р const) избыточная энергия электрической системы может быть оценена по бапансу реактивной мощности: Q = Qµ +Q.. (12.45) Составпяющие (12.45) описываются уравнениями (12.15), где независимой переме1111ой режима явпяется напряжение в системе Qµ = ll.Jxµ при ct =О; (12.46/· Q, = с1, (х", +х,), [(х", + х,)' +r2.ts2]. (12.47 '
ноет-и: аадаются скопьжениями s и паходят вначения тока, соответствующие иеиз- Qкр менной нагрузке Р = coпst, по формупе Р = 1• (r2/s); flo по полученным значениям тока вы- о- ----.. чнсляют ряд напряжений Uc.lfp llto ц.
где По найденным значениям напряжения определяюг состамяющие (12.45). Жен11я в системе
При ВКJ\ючении в узле нагрузки статических компенсирующих конденсаторов мощностью Qи и сопротивпением х" = U'!Qк (см. рис. 12.7, 6) вначаJJе определяют сопротивпение эквивалент ного шунта (см. рис. 12.7, в) nl> формуJJе ixw = - fxкjxµl(jXµ - jx.),
по (12.43) при усповни Хµ Xw· Графический аналнз зависимости Q (U.) по составпяющим Q и Q, (рис. 12.9) локазывает, что предепьный режим с критиче скими значениями параметров Uс.ир, Q.p соответствует критерию · dQldU. = -оо. Схема электроснабжения с эквивапентным нсточникш, питаю щим комплексную наrрузкУ соизмеримой ыощности. Э-rу схему и схему электроснабжеиия крупного yзJJa нагрузки можио предста вить схемой замещения. показанной иа рис. J.2.1О, а. В точке вклю· чения нагрузки состояние равновесия характеризуется изменяю щимися параметрами режима U, Р" = F, (U), Qи = F,(U). Вдаином _
случае сво6одной существенной переменной лВJ1яется напря жение в yЗJJe оодключения нагрузки, которое отражает соСТОJJНП6 JJCex элементов системы. Изменение в переменных параметров ,режима можно зафиксировать по показателям режима Еsк и Q.к, по которым косвенно судят об избыточной энергии системы при е возмущении. Графический анализ sависимости Еэк - V(U' + Р"г,. +Q"х.к)2 +(Р"Хэк -Q.r")2/U (12.48) .с утяжелением режима по переменной U 11оказывает, что она имеет минимум при dE.,,/dU = О с координатами, соответствующими пре .дельному режиму Е" mtn, и•• (рис. 12.10, б).
_f'н=f,(IJ)
'!}j«o Е"{/1) ЯЖ->о
то они соответствуют экстремальной точке (Е".••• Q".кр) критерия (12.49) при (рис. 12.10, в) dQ.кfdE,. = - оо. (12.51) При проверке устойчивости по (12.51) также выполняется утя желение режима по переменной U и состоянию устойчивости со ответствует участок кривой, представт1ющей зависимость Q" (Е••), с критерием dQ"/dE,,. <О. (12.52) Коэффициент запаса статической усrойчивости дJIЯ узла вклю t.Jения нагрузки определяется выражениями Кзv =(Ио -Uнр) · 100/U0; Кзе = (Е о -Еж.кр) · 100/Е"о. Таким образом, статическая устойчивость СЭС может быть най дена по практическим критеринм только для конкретной схемы н при принятых допущениях. При этом анализ устойчивости про водят в несколько этапов: состамяют схему замещения СЭС, устанавливают массив из E.11tmin -""' """:::....,!fff!=o (1/) меняющнхс}I параметров режима и принимают основные допу щения; в массиве переменных выделяют существенную независимую 01---- --'""--- //1/кр Uo и 0 / 1Рнс. 12.IO, Схема замещення СЭС с комплексноn нагрузкой (а) и эавliс•1мо .ст}f ее существенных переменных (б, в)
Можно провести параллель идентичности физической картины s1poueccoв сохранения устойчивости комплексной нагрузки н асии J<ронной нагрузки, описываемой рис. 12.8. При Е" = Е.ко рав :нооесие установившегося режима возможно в точках а и Ь (см. _рис. 12.10, б) аналогично точкам равновесия режима на рис. 12.8. В точ"е а производная dE,JdU >О, что на угловой характерис тике мощности соответствует устойчивому равновесию режим.и. С утяжелением режима по переменной U каждой точке кри '1\оЙ Е"" (И) соотоетствует увеличивающееся скольжение по -рис. 12.8. При критическом значении скольжения имеет место крити "lеское напряжение и". Точка Ь, где nроизводная dE""/dU < О, соответствует no угловоft характеристике мощности неустой•1ивому равновесию уста11овившеrося режима. Слеловательио, знак производной dEldU позволяет судить об " устойчивости системы. Критерий устойчивости dE/dU>O (12.49) впервые был предложен проф. П. С.)1\дановым и называется кpurм p1t eAt усrrwйчивости Жданова. Если 011енивать координаты предельного режима сохранения статической устойчивости по (12.48) и зависимости Q" = Q" + (Р;, + Q,)x"/U', (12.50) переменную, 1юторая определяет сос-rояние всех элементов СЭС; устанавливают существенные переменные, по которым косвен но можно оценить избыточную энергию системы при ее возму щении; онределяют взаимосвязь существенных переменных для уста новившегося режима; по практическим критериям находят координаты предельного режима coxpaнel!иfi устойчивости; выбор существенных перемен ных онределяет путь утяжеления режима; рассматривают запас статической устойчивости, который сравнивают с нормируемым.
12.З. Исследование статической устойчивости методом малых колебаний В установившемся реж1-1м:е СЭС знаt1ения ее нарамечюв под воздействием разных факторов, главным образом нагрузки, изме няются около состояния равновесия. Когда параметры режима получают приращения, которые несоизмеримо малы по сравнению с установившим11с)1 их значеинями, такие воздействия на состоя ние равновесия относят к слабым возмущениям. Если СЭС описывается уравнениями невысокого порядка, то д..1я оценки статпческой устойчиnости режима можно использовать метод малых КОJJебаннй. В отличие от оценки статической устой шюсти по практическим критериf1М суть этого метода заключа ется в нсспедовании уравне11ий движения, записанных в виде урав- 11е11ий малых отклонений.
Пусть состояние СЭС в любой момент времени описывается дифференциальным иели11ейным урав11е11ием возмущенного движе ния вида
ва, после чего анализируется вид корней характеристического урав нения системы линеаризованных уравнений. В основе линеари· sацин лежит предположеине о таком изменеиин переменных в пе реходном процессе, при котором и:х откпопения от установившихся sначеиий остаются все время достаточно малыми. (12.53) где у, -совокупность показателей режима С, которые явля т ся функциями времени; / 1 - внешние воздеисmия, изменение ко торых может быть произВОJJьны м. Линеаризацию системы уравнений (12.55) выполняют разло жением левой части уравнений в степенной ряд (Тейлора или Мак .парена) по степеням малых отклонений х1 (все пронзводиые от х, р ссматриваются как самостоятельные переменные): В состоянии равновесия СЭС характеризуется установивши мися значениями (у1О) этих показателей: У0 (1, У10, О) = F0 (f10. О). (12.54) У0 (t, у10) + (дУ/ду;)"0 х, + (дУ/д (d'y1/dt'))u 10 s"""l + <х1 = F (/,, d 1f /dt 1 (d'x,/dt') +
При F0 (/10, О) = О возмущающие воздействия являются про·
Здесь К п 1). (12.57) ходящими (предполагаем, чтu они пре1<ращаются при t = 10). Тогда уравнение (12.54) описывает невозмущеиное движение. s,1 = 1: (if'Y!д(d'y,Jdt')'Jv 10 (d'x,/dl) + (ifYtд!li)" 0 x1 (12.58) Левую часть урав11ения (12.53) можно выразить через малые Отклонения х1 = у, - Yto пок"зателей режима у1 О'! установив k ='l s=1 k=-2 - сумма членов, состоящнх из произведений частных производнь:х (второго и высших порядков) от функции У н малых отклонении, шихся значений YtfJ, записав у (t. У10 + х,, dk (У10 +X1)/dt") - F (f,. d'f,/dt'>· (12.55) а также их производных; (дУ/ду1)щ 0 = й1п, (дУ/д (d'y,ldt'))u,0 =
Здесь состамяющие, кmорые содержат х1, характеризуют переходный процесс Х (t), вызванный возмущениями. Начальные условия для переходного процесса при t = to х,(10) = х10 = Y{(f0)-Y1o(l 0). (12.56) В случае невозм ущеuного движения х, """ О. Оценка устойчивости на основе систем уравнений вида (12.55) обоснована теоремами А. М. Ляпуно ва. Невозмуще11ное движение будет устойчивым по отноше11ию к показате.пям у1 (f), если при вся ком зада1111ом положительно м числе е, как бы мало оно ни было, = а1, - коэффицненты при переменных х1 и tfy1/dt' (их значе н11>1 вычисляются по выражениям частных производных фуикции У по у, в точках У10)- Есди из уравнений (12.57) вычесть уравнения равновесия (12.54) и пренебречь суммой ч.пеиов степенных рядов s,,, то получим лине аризованные уравнен11я возмущенного движения (уравнения перво го приближения) ·-· (дУ/д (d'y 1/dt'))y 10 (d'x,/dt') + (дУ/дудv1.Х1 = можно выбрать та1<ое другое положнте.пьное число '1] (в), при кmо· = F (f,, d'f,/dl1)-F 0 (/;о, О). ром для любых начальных условий от возмущений х, (10), удов.пе творяющих 11еравенствам 1 х1 (10) 1,;;;; •J, дл>J t > 10 выполняютс неравенства 1 х, (t) 1 < в.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.013 с.) |

 Vдв - / V + (r,/s)2; / VJ Jf(x,к + х,)1 + (r2/s)'.откуда
Vдв - / V + (r,/s)2; / VJ Jf(x,к + х,)1 + (r2/s)'.откуда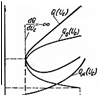 I<ритнческие параметры системы ш1ре q деляюгся на основе анапиза (12.45), ко торый ВЫПОJ1НЯЮТ в такой поспедоватепь-
I<ритнческие параметры системы ш1ре q деляюгся на основе анапиза (12.45), ко торый ВЫПОJ1НЯЮТ в такой поспедоватепь-


 tJo=const а Гин=Fz(I/)
tJo=const а Гин=Fz(I/)


