
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двигателя описывается уравнением движенияСодержание книги
Поиск на нашем сайте
Т,ds/dl = М (s) -А1мх- (12.12) Здесь э.тrеt..-тромагнитный момент двигателя относительных ед.и· ницах М (s) = 2tnm"U.f(s/s,0 + s,0/s), (12.13) PJ!C. 12.2. Г разная сжема 3а\1еще11ия асин>еронноrо дншателя (а) JJ схема за 1ешения участка!:Jлектр нческой сет11 (6)
Параметры двигателя для Г-ООразной схемы замещения опре деляются rю каталожным данным с а.1слользованием нижелриведен иых выражений. Активное сопротивление, nропорщюнальное механическому мо менту на валу ·двигателя и определяемое при равном числе витко• обмоток ротора и статора,
'2 = [r,0 (1-s)+r21 (s-s1)J/(l-si), s>s1· Индуктивное сопротивление рассеяния статора и ротора х,о, s s1;
XsJ, S S2° Поправочным коэффицие!ПОМ а учитывают 11асыщенне главноi• магнитной цепи двигателя. С учетом насыщения а = 0,3, без уче та -а= О. Ориентнровоч11ые «0nорные» значения скОJJьжения s1 Р' Sz --=. = 0,5 -;- 0,9 11ри кусочно-линейной аппроксимации -характерист11к двигателя х, (s) и r 2 (s). • Координаты «опорных» точек аппроксимируемых характери Х,,о l/(2mmax COS <р,..,); Х,1 = Хµ/(fпу«Хµ - 1); 2R7" r 20 = S.ю• (1 + V 1 - 11т;',,.,)J(2 ros 'Р•ом); r21 = ( 1 - v 1 - 4fs1m ycк COS2 (J>мм)/(2тпусн cos Q'ном). где l11уск. m11yc1c = Мпускf Мном - кратность пускового тока н момен" Та соответственно. Conpom в.ne1111e намагничивания можно рассчитать по форыуле Хµ = 1J{siп<p"0"-(I- V 1-4х соs2 <ри0.}/(2х.о)). Момент сопротивления для большинства вращающихся рабочих механизмов выражается зависимостью [24] м •• = м••.ст +(М••о-М••.от) ((1 -s)/(I -s"0.))", (12.16) rде Мм t.ст - начальный (статический, ro = О) момент сопротивле яия; Ммхо - номинальный момент сопротивления механизма; р - показатель степени, зависящий от типа оборудования [27]. В уравнениях движения элементы электрической сети (узлы, ветви из ЛЭП, трансформаторов и т. n.) описываются по-разному. Для узла сети с п ветвями должен выполняться баланс активных 11 реактивных мощностей: n Вид уравнений движения нагрузки зав11сит от прин11ыаеыой расчетной модели ее узла -группы разнородных злектроnрие м ников, присоединенных к узловой точке сети. Расчетная модель нагруз1<и предприятия определяется составом потребителей и его распределительной сетыо. В общем случае она ыногоэлементная, где каждый узел нагрузки содержит матемll'l'иЧес1юе описание экви· валентных параметров асинхронного и синхронного двигателей. а также статической нагрузки zн (освещение, выпрямители, инвер торы. электропечи, нагревательные приборы, коммунально-бытовые электроnриемиики, конденсаторные батареи и т. п.).
В математическом олнсании р асчетной модели нагрузки исrюль зуют статшш:кие и динамические характеристики. Они представ· ляют собой зависим.ости патребляемой yЗJJoM нагрузю1 активной и реактивной мощностей, вращающего момента или тока от напряже ния и частоты. Статические хара1сrеристики нагрузки Р" F, (U, w); Q" = F, (U, w) (12.19) определяют вариации Р н• Q" при медленных изменениях напряже ния и угловой скорости. Задание нагрузок в виде оостоянных сопро· тивлений z. = coпst с,1едует рассматривать как частный случа_й статических харакrеристик. " Р,=0; I-1 L Q,=O. l=I (12.17) Динамические х арактеристики нагрузки -это зависимости o'r тех же аргументов н, допоJнштельно, от- скоростей их изменения: Э.пементы веrnей сети в схемах замещения лредстав.няются в виде последовательно-параллельно включенных активных и реак тивных сопротивлений. Параметры режима электрической сети опре· деляются с учетом потерь напряже11ия н мощности. Например, Р = F8 (V, "'· t, dU/dt, dw!dt,..•); 1 Q = f4 (U, "'· t, dU;dt, dwtdt, ".).
(12.20) участок электрической сети на рис. 12.2, 6 описывается следуюшимн уравнениями: В начале участка Р, = Viy11.sina11 + U1U,y10 sin(<\2 -a12); (12.18, а) Q, = Uiy11 cos а11 -U1U2y12 cos (б12 -а");
Q, = -Uiy22 sina22 +U,U,y1,cos(б12 +а12). Эги характеристики позволяют отразить быстрые изменения ре жима _нагрузки. Выбор вида характеристики нагрузки предопределяется н.еобхо димой точностью реше1щя задачи усТойчивости. В приблнжениых расчетах устойчивости СЭС наиболее часто используется модель на грузки в виде комплексного сопротивления. С использованием мате матических моделей элементов строится модель вceii СЭС. С точки зрения выполняемых упрощений математические модели системы можно подразделить на консерва11и1внш позиционные и дис· Р, -U y" sin a22 + U,U,y 12 sin (б12 + ""): сипативные [7]. Описание системы консервативной позишюнной
(12.18, б)
Здесь собственные и взаимная проводимости опреде.r1яются выра жениями У11 = l/(21 +2,,23/(z, +Zз)) =Ун ехр <Р1.1; У22 = 1/(z, +z,z,!(z1 + 23)) = У22 ехр <р,,; У12 = li(z, +22 +z1z2/z3) = у12 ехр <р12, А доло..111ите.,1ь11ые у глы сх11 = 90° - Ч'н; СХ22 = 90'.) -fP22; СХ12 = 90:> -(J>1a· моделью соответствует допущениям, в соответствии с которыми в системе отсутствуют nотерн энергии, зависящие от частоты враще ния машин (значит, любые возмущения режима приводят к незату хающи м. колебаниям), а все действующие моменты не зависят от- из менения частоты вращения машин, за исключением тех, которые связаны с инерционностью роторов. Поэтому при позиционной идеализ щии в уравнениях движения моменты в относительных единицах мож110 заменить мощностями. J\\ощности турбин, э. д. с. машин, частота и сопротивления пассивных элементов электрнче· ской сетн принимаются постоянными, а электромаrнит11ая мощнш..".1ъ вависит только от положения роторов синхронных машин. }Q 8.:_ З7БЪ 289 В диссипативной моде.пи системы учитывается, что моменты ма шин эав11сят от положения роторов и скорости их изменения, в также от 1юказателей, определяемых разпиЧ1Jыми сис-1·емами регулирова· ния. электромаrnm11ыми и электромеханическими nереходными nро цессаьш в элементах.
иых процессов на основе позиционной модели приемлем для анализа устойчивости С.ЭС предприятий. При централизованном электро· снабжении в СЭС все1·да есть шины бесконечвоii мощнuсти (уСJJовне неизмеиенносrи напряжения и час-НJ"i'ЬI). Кроме того, задача усrой чивости решаеrся на малом интервале nремен11 (до 0,2-0,5 с) от начала действия возмущения. При этом определяющими в отноше нии устойчивост t являются синхронпзнрующие моменты, а ииер ционные моменты, заuисшдие от частоты вращения, пронв11яюгся незначительно.
12.2. Практические критерии оценки стати•1еской устойчивости Ана.nиз статиt1еской устойчиrюсти по его возрастающей слож ности можно ра збить на несколько этапов. Вначале следуеr YL"ra· навить факт наличия устойчивости или 11еус1·ойчивости установив шегося режима, а затем по Еиду кривой или друп1м признакам различить хараr<тер переходного процесса (апериодический или 1шлебатель11ый). Физически апериодическая неусrойчивость возникает при нару· шенин баланса моментов на валу генератора, когда механиоrеский момент турбины оревышает максимально возможный при данных условиях электромагнитный момент генератора. Анализ устойч11- вости заключается в определеиии предельных 110 устойчивости ре жимов Jta основе сползания или текучести параметров нормального режима с использованием уравнений установившегося режима. На следующем этапе для установленной области устойчивых режимов выяв.пяются условия колебательной неустойчивости. ко торая можеr появиться по следующим причииам: из-за наличия парамеrрическоrо самораскачивания или обрат ной связи в виде АРВ; при возникновении самовозбуждения, когда синхронный гене ратор нагружен емкостью или лннией с распределенными парамет· рам и; из-за неустойчивости нагрузки. Анализ колебательной устойчивости предполагает учет дина· мнки элементов системы посредством ее модели, описываемой диф· ференциальными уравне11иями. При этом ствщrrся и решаеrся за· дача определения структуры и парамеrров элементов регулирую
щих устройств для обеспечения статической устойчивост и режимов системы. Наличие усrойчивости или неусrойчивости уеrановившеrос11 режима при относительно ма11ых текущих изменениях его парамет-
ров («сползаиии• локаза1елей установившегося режима) можиоонре делить с помощью практических критериев, основанных на физиче ских nредставпеииях о механизме нарушения устойчивости. Они применяются в тех случаях, когда отсутствуют условия самораска- 1Jивания и нет необходимости в исследованиях характера nереход ноrо процесса и в выявлении формы нарушения устойчивости (апериодическая илн колебатеJJьная). Оценка устойчивости по прак· тическим критериям является грубой, завышенноИ по запасу устой чивости и устанавливаеr лишь сам факт устойчивости данного ре жима. Физическаи оценка механизма нарушения устойчивосп1 вьшол няется на основе си;ювого или энергетического 11одхода. При акер гетичвсКlМt подход услоuия устойчипос ти определшотся соглас110 теореме Дирихле, R соаrве-rс-1·вии с которой система будет устойчи вой. если потенциальная энерn1я консервативной системы в поло жении равновесия имеет минимум. При силово1tt r:юдходе устойчи вость сист мы определяется условием, согласно которому в nnложе ии11 равновесия сумма приложенных к телу сил должна быть равноii нулю. В случае отк1юиения тела от положения раuновесия должна возникнуть сила, стремящаяся вернуть его в ло.nожение равновесия. Если в лоложении равновесия те.тю имеет скорость, то возникающие нри этом сиJJы должны быть напрамены против век· тора скоростя. В основе применения практических кр1rrернев статическоii устой чивости СЭС лежат оцеики ее свойств по энергетическому критерию (11.12), который устанавливает соот11оше11ие между интенсивностью внешнего воздействия 11а систему и ее реакцней на это воздействие. Он предусматриваеr определение избыточной энергии во всей систе· ме в целом. Оценка статической устойчивости по практическим критериям позволяет установить предельный режим и границу устойчивости при выбранном способе воздействия на СЭС. Послед11ий называют способом утяжеления режима. Он может быть выбран только при условии, если заданы схема электроснабжения и состав электро приемников. Расчетные схемы электрос11абже11ия могут приволшься к раз- 11ичным видам: эквивалентный генератор -ЛЭП - шины неизмешюго напря· жения; двустороннее J'штание нагрузки с постоя1111ым соnротнВJ1ением; эквивалентный 1-1сточник питания -узловая точка сеrи; питание асщ1хроиной нагрузки от мощной ЭЭС;
эквивалентный источник, питающий:ком11лекс11ую нагрузку со· измеримой мощности. Рассмотрим характерные примеры использов2ния практических критериев для анализа статической устойчивости Э'Гих схем. Схема злектроснабження «Зквивалентный генератор -ЛЭП - шины иеизмеиноrо напряжеииn». Эrа схема с nараметрами ее эле ментоЕ показана на рис. 12.3. В уста ювившемся режиме механи- 19* 291 ческий момент турбины и электромагиитныn момент генератора уравновеш ены, т. е.
где
z11 jx, + jx,z,,/(jx 2 + zн) = 1>н1 ехр (л/2 -а11); Мт-М=О, где электромагнитный момент М = E'U siп б/(ы,, (х +х")) (12.21)
(12.22) z,. = /х1 + jx, + jx,jx.,Jzн = 1 z" I ехр (л/2 -а12) = R" +;х12• В уравнениях (12.25) свободной существенной переменной, от которой зависят изменяющиес11 параметры режима (Р, U0), является угол б12• Поэтому производную dP!dб 1, можно 11спо.льзо имеет только од 1у существенную переменную б, так как другие параметры (Е', U, ы0) оо условию неизменны. Механический ыо мент турбины, как следует из (12.7), не зависит от переменной б. rf АJП т;, Выражая параметры сн- IБ\ l · стемы в относительных еди- ,!. ··· P,Q ницах и считая ее частоту ие- ;опst rвк $;': %JJ/ изменной, можно принять P,,Q, М ""' Р и представить урав- вать в качестве практического критерия статической устойчивости анаJЮГИЧIЮ выраженl\Ю (11.17): dP/dб12 >0. (12.26) Предельный 1ю сохранению устойчивости режим соответствует условию
откуда Рис. 12.З. <..хем а злек1роснабження «экпн- нение (12.21) n следующем валентный генератор -ЛЭП -шипы не- ВJЩе: б12кр = n/2 +arctg (R12tx"). (12.28) нзменного наnряження» Р,-Р = О. (12.23) (Подставив (12.28) в уравнение активной мощности генераторной станции (12.25), получим критическое значение переменной режи Графическое изображение (12.23) в зависимости от перемен ной б (см. рис. 11.9) показывает, что существуют две точки равно весия режима системы. Нарушение равенства мощностей (12.23) является признаком изменения ее энергетического баланса и появ ления избыточной зиергни в системе. В этом случае эиергетическнn ма для угловой характеристики мощности: Pmox - Е 1 sin a11/I Z11 I + E.1E<121f z12 I. (12.29; Коэффициент запаса статической устойчи1ЮСТп определяется выражением критерий (11.12) можно записать так: d(Pт-P)fdб<O. (12.24) Поскольку Рт (б) = coпsl, неравенство (12.24) принимает вид
к.= (Ртах - P.)JP". Схема замещения алектрической систе- Е91:z,r мы, содержащая узловую точку. Ан а. шз этой схемы (рис. 12.5) упрощается. Объяс- -Е,2:z" няется это тем, что нагрузки, подключен-
(12.30)
1:1.51U') )> f!."=!;Jl } замещать части системы изадаваться стати- Q>.:'--C:J---4Ux fМ\_!_AJЛf '9П2 f...... о\ E11r=cмst • Erz=cмsf ческими (12.19) или динамическими (12.20) характеристиками. Узлы характеризуются ве1{торами 11а11ряжения. ко1орые играют
Рве. 12.5. Cxe-'ta заl\·1еще ния 9лектрической систе мы с узловой точкоii Р,, Q1-'11- Vн _zн=HнlJ.rн -1.r1z
t-'нс l;t.4 Схе 1а двуст0роннего ли;аиня нагрузки (z11 = const)
Схема с двусторонним питанием нагрузки. Для этой схемы, им<"ющей rюеrоянное сопротивление нагрузки (рис. 12.4), знергетиче синй критерий (11.12) можно косвеuно характеризовать переменной
режима - активной мощностью. Если допустить, что генераторные ветви имеют одинаковую нагрузку (Р, = Р, = Р), то установив шийся режим будет описываться следующей системой уравuений: Р-Р, =0; } Р =: Е:, siпa;,11 z11+ E.,EQ2 sin(l!12 -a12J/I z"1; (12.25) Р, т 12 -U"JR. -U, роль эквивалентных э. д. с. неявных источ- 1шков и нагрузок и отличаются от янных тем, что они нс обладают инерционностью генераторов н нагрузок двигателей. Практнческий критерий статической устойчив ости режиме рас сматриваемой системы можно сформу.1ировать 11ри неизменной частоте, сохранеияи баланса г.н·пш1юй мощности в узле и nостшш стве активной мощности, nередаваемой из rенератор1-1ыJ; ветвей (Е, Р = coпsl). Из аиализа множества изменяющихся 1 арам1ечо" режима (Е, Р, Q, U,, 11) следует, что суще<..-твенной не.,ав1ю;мо>1 переменной, оnредеJ1яющей состошtие всех э.пемепrов системы, ямяется напряжение в узловой -,очке U, = vаг (переменна" б в данном случае не существенна, так как она не олределяет состои ине нагрузки). Избьrrочная энергия системы, возникающая из-за оозмущаю_: щих воздействий, проявляется как изменение баJ1анса реактиnнои 292 293
"
(12.31)
имеет узловую точку неизменного напряжеиия илн точку, nнтаю щуюся от эквивалентного нсточннка с неизменной э. д. с. Ее схема замеще шя показана на рис. 12.7, а, где нагрузка лредставлена где Q,, = Q,1 - суммарная 1·е11ерируемая реактивна" мощ l=t llOCTb В уЗJ]е.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.123 (0.009 с.) |

 Упрощенный подход к расчету электромеханических переход·
Упрощенный подход к расчету электромеханических переход·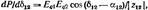 (12.27)
(12.27) (11.17).
(11.17). ные к узловым точкам сложных еэс. могут l.л:см
ные к узловым точкам сложных еэс. могут l.л:см



