Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Телы1ых едниицах можно за1шсать в видеСодержание книги
Поиск на нашем сайте
Телы1ых едниицах можно за1шсать в виде Р, = Р,., + Рnот + т,(d2б!dt') + Pd(dбidt), (11.1) где Р, - мощность турбины, опреде,1яющая исходный установив шнНся реяшм с11сrемы (Рт = Р0); Рзл - элсхтромаrнитная r..Ющ ность генератора; Рnот - потери в агрегате; Р. - демпферный коэффициент; б - угол, определяющий пространственное положе
Щ,ихся.шее турбины и генератора, причем Т.1 = GD°i:11.,n..,.,/(91 · 4Р,...),., GD 1iY(364P00). (11.2) Здесь G - масса подвижных элементов; D - суммарный диа метр подвижных масс; n0 и nном - синхронная и номинальная ча
Маховый момеит. Выражение (11.1) называют уршJНеiш ем электромеханиче ских nереходlШХ 11роцеаюв. Если потерями мощности в агрегате и по терями в демпферных контурах пренебречь, то это уравнение при Мет вид
Форма записи уравнения (11.3) зависит от того, в каких еди ницах выражаются входящие в него велнчниы (табл. 11.1). При Р, - Р,, <О имеет место тормозящий момент, а пр11 Р, - Рм >О - ускоряющий момент. Торможения или ускорения роторов генераторов являются СJ1едствием набросов и сбросов на грузки. Возникающий при этом небаланс МОЩНОСПI поI<рывается Зи счет энерmи вращающ11хся масс. На устойчивость нагрузки существенное влияние оказывает Изменение частоты 1З ра1цения. Потребляемая электродвиr ате..1ямн
'
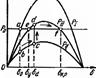
1 """'' 1 :J f"м f о l,ш1 f Рис. 11.1. Зависимость реактив. Рис. 11.2. Статичесl\ис Ст частоты энергетической системы
активная (тормозная) мощность при номинальных значениях сколь жения, коэффициента загрузки н без учета псrrерь зависит от ча стоты:
или Р,-Р,., =Т.1 (d'l\fdt2),
Р, -Р., = TJ(dU>ldl) =; Т,а., (11.3)
(11.4)
Физически это означает, что лри отклонениях частоты враще ния двигателей с измененной угловой скоростью (U> = vаг) нужно изменять а1<7ивную мощность. где "'-угловая скорость; а -углоnое ускорение вращающихся масс_
Ве.nн•шны
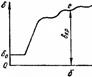
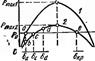
Vравнею!I! Угол ll Зависимость реактивной мощности двигателей аг частоты вра Щения определяется выражением Q.'Q2 = (f.tf2)". " = 1 -7- 2. (11.6) С повышением частоты намагничивающая мощ11ость Qnaм падает, так как уменьшается 11асыщение, а мощ11ость рассеяния Q ac уве личивается (рис. 11.1). Для энергетической системы в целом зависимость аитивной Р и реактивной Q мощностей от частоты вращения генераторов Рт-Р 3л = TJ (d26ldt2) Рт-Рзл = TJ (1)1) (d26.'d Р"-Р = TJw0P0 (d'Mdt"') Р"-Р,,= Т1Р 0 (d'{;ldt')/w0 Р"-Р,., = Т.1Р 0 (d'б/dt')/(360f 0) рад рад рад ОТП. ед. рад рад отн. ед. рад рад с кВт рад с кВт вл. град с кВт выражается посредством статических характеристик (рис. 11. 2). Мощность, развиваемая турбиной, зависит от массы пропуска Емого через нее пара или воды в единицу времени и может нз меняться с помощью первичных регуляторов, которые обладают статической или астатической характеристикой (рис. 11.3). Рт - Р эл = ТJ (d'б/d/2)/(360f 0) Зл. град с отн. ед. рад с отн. ед. Статизм регулятора характеризуется коэффициентом статизма Р, -Р" = Т1О>о (d'{;fdt')iP0
ра.ц рад кВт-с orn. ед. рад оти. ед. Кст = Лf/ЛР = Л11/ЛР = tga. (11.7) Первичные регуляторы частоты вращения 11меI01 естественную
Из определения устойчивости следует, что ус.аовием сохра 'fiення устойчиВОС7И сис-rемы (критерием устойчивости) является охпношенне Из схем замещения рассматривае юй электропередачи (рис. 11.7, б. в) следует, что результирующее со11ротивление х.,,,, = х. +Хгр1 + х,,/2 + Хтр. (11- 13) ЛW/ЛП>ЛW,/ЛП, или в дифj>еренциальной форме d(W,-W)idП<O. (11.10)
(11.11) !Зектор<Jая диагра'1ма для нормального режима работы этой !'1ектропередач> показана иа рис. 11.8, откуда видно, что Ьс = Е. Х Х sin б, или Ьс = /Хлреэ cos (fJ = l irX'dpeэ· При этом
Величину W, - W = Л W, называюг избыто«ной энергией. Эrа энергия положит ельна, ес 1и дололнительная генерируемая энергия, nоявившаnсл при возмущении, возрастает интенсивнее, чем нагрузка <системы с учетом потерь в ней. При этом условии 1 ритер шi устоНчивости запишется D онде d(ЛW>J.1dП<O. (11.12) -т. е. режим устойчив, если производная от избыточной энергии ло определяющему параметру П отрицательна. Для обеспечения статичес1шй устойчиюсти системы сущест zеиное значение имеет запас с·1·атическшi усrойчивостн. который Eq sin fJ = 111Хdрез
Рис. IJ.7. Схема электропередачи (а) и схе!\.1Ы ее замещения (6, в) (11-14) ()Пределяет допустимые пределы ухудшения режима до наруше .ння стаmчесиой устойчнвосm. Запас статической устойчивости •может характеризоваться углами сдвига роторов генераторов и .11аnрлжениями в узловых точках системы.
чивости в нослеаварийном режиме, который уменьшается по сравне Умножив обе чac-rn рацнства (11.14) на Uclx.,..., по.пучим акп1вную мощность, лер аваемую приемной системе: Р = E•Ucsin6!x.,.." (11. 15). где EQ = V (Uс + f pXdpeo) +(/,Xdp"), Большое значение имеет наличие запаса статическое устой
нию с запасом статической устойчивости в нормальном режиме, причем в последнем запас устойчивости по увеличению мощности элеl(трической передачи должен составлять 15-20 %, а в после ; варийном режиме - 5-Ю %, но эти з11ачения строго не лимити руются: Чrобы проверить статическую устойчивость системы, необхо димо составить дифференциальные уравнения малых колебаний .д.1я всех ее элементов и регулирующих устройств, а затем исследо вать корни характеристического уравнения на устойчивость. По rСl<Ольиу строгое решение такой задачи очень сложно. в инженерных: ;расчетах применяются приближенные методы исследования устой чивости, которые основываются на исnодьзовании праr<Тических "ри-rериев устойчивости. • Рассмотрим простейшую схему элеюрическои передачи, в ко торой генератор работает через трансформатор и линию на шин: неизменного напряжения, т. е. на шины системы, мощность 1<оторои 11астолько велика по сравнению с мощностью рассматрш а мoll элек трической передачи, что напряжение иа ее шинах можно считать неизменным по амплитуде и фазе при тобых режимах (рис. 11.7, а). При исследовании характера переходного процесса удобно пользоваться углооой харак-rеристикой Р ""' f (6), где Р -электро магнитная мощность генератора; 6 - угол сдвига rю фазе между синхронной э. д. с. генератора Е. и напряжением на шинах прием ной системы U с· 2 2 или Е0 = V<Ис + Qx."",JU.)' + (PXdpe>!Uc)2•
системы Ис изменение переда- о..,-,;=----'--_. _,,.=::.., ваемой мощности Р зависнт лишь от изменения угла б. Рис. 1J.8. Векторная диаrра tмв для иор- Мощность. отдаваемую ге- мвльноrо режима раfuты электропередачи нератором в сеть, можно изме- нить также воздейств11ем на регулирующие клапаны турбины. В ис ходном режиме МОIЦИОСТЬ rурб1шы урщшовешиnается мощностью rе нера тора, раоотающеrо с неизменной частотой вращения. По мере от1<рытия регулирующих КJ а11апов (или направляющего аппарвта у гидротурбин) мощность турбины нnэрастает, в результате чего равновесие вращающего и тормозящего моментов турGины и гене ратора нарушается. что вызывает ускорение вращения генератора. При ускорении генератора вектор э. 11. с. f:; перемещается от поен:-е.пыю вращающегося неизменйой скоростью вектора напря жения приемной системы Ос. Связанное с этим увеличение угла 6 приводит к соответствующему повышевl'но мощности генератора по синусо111альному закону J1IJ тех лор, пока она вновь не уравнове- 18 8-З75Ь 273
сит возросшую мощность турбины. Поскольку зависимость Р = = f (6) носит сннусоидапьный характер, с увеличением угла 6 мощ ность Р сначала оозрастает. а затем, достигнув маисимальноrо значения, начинает падать. При эада ш-1ых значениях э. д. с. гепер а1·ора Ец и напрн ження приемника И, существует определенный ма,симум передаваемой
режим в точке а. Слеювательно, данный режим системы является усrойчивым. К этому же выводу можно прийти и при отрицатель ном пр11ращени11 угла Лб в точке а. В точке Ь на рис. 11.9 1юложительное приращение угла ЛЬ сопровождается отрицательным изменением мощности генератора ЛР. Уменьшение мощности генер атора вызывает появление ускоря о;I;а;:Ы 3 в: e:;::<lJ:Ы; i: MOЩflOCmU. С 6 ющего момента, под влиянием иоторого угол б не уменьшается, а
увеличением угла мощность генер атора продолжа· Р"" = E.VJx"'* '· (11.16) Графическая зависи 1ость активной мощности Р от угла 6 nо ка ана на рис. 11.9. В установивше'1сЯ режнме мощность турбины Р0 равна мощ ности генератора Р, т. е. между неизменной мощностью первично го двигателя н мощностью генератора существует равнов есие. Пр и этом каждому значению мощности турбины Р 0 соответствует д.Ве точки равновесия на угловой характеристике мощности генера тора (см. рис. 11.9) и, следовате.nьно, два значения угла (6u н 6.).
движен ия ротора геператора при небольшом отклонении от точек рапновесия (рис. 11.10).
ет падать, что обусловливает даJ1ы1ейшее увеличение угла 6 и т. д. Процесс протекает прогрессивно и генератор выпадает из синхро· низма, т. е. режим работы в точке Ь статически неустойчив. Таким образом, состояние генератора, сооwетствующее точке а 11 любой другой точке на возрастающей части с11нусо11дальной ха рактеристики мощности, статически устойчиво. а состояние ге нератора, соответствующее всем точкам спадающей части харак теристики, статически неустой•1иво. Отсюда вытекает следующий критерий статической устойчивости системы: ЛР!Лб>О, ИJIH dP/df>>O. (11.17) Из (11.17) следует, что статическая устойчивость системы обес печивается, если приращения угла 6 и мощности генератора Р имеют один и тот же знак. Производную dP/dб = Sв 11ринято называть синхронизирующей .11 ющностью. Эта мощность хара1<теризует реакцию генератора на увеличение угла сдвига paropa. Положительный знак ее является критерием статической устойчивосrи. Есnн АРВ отсутствует, то сннхрониз11рующая •ющность опредедяется выражением SE=(dP:dl>)E_ c.,. • = E.Vccos6/ xd,.." (11.18) При 6 < 90" синхронизирующая мощность rюJюжител ы а " обеспечиваются устойчивые стационарные режимы раба 1ъ1 системы
харi!ктер и стнка и ХВJJактеристика синхро низирующей,..ющности генера тора Рис. 11.1О. Изменение положе· ния J'ОТора генс1Jатор.а nри ма лом возмущении (см. рис. 11.9). Количестнеи110 статическая устойчивость харак теризуется коэффициентом запаса К, = (Р"., -Р0)/Р0, где Рта х А Р0 - ма1<:сю.1альная и IЮ!\.ШНа.лLная мошности системы. ствует nоложителрное приращение мощности. В результате увеличения мощности генератора при неизмен н ой мощности турбины равновесие вращающего и тормозя щего моментов турбины и генератора нарушает ся, и на валу машины ноэ- 11икает тормозящиii момент. Под его м11я1шем ротор генератора начинает замедляться. что обусловливает 11еремещение связа11но го с ротором вектора э. д. с. генератора -а сторону уменьше1111я угла б. С уыеиьш еш1ем угла 6 вновь восстанамивается исходный
11.3. Динамическая уеrойчивость
Электроэнергетичесю1н система динам1-1ч.t:ски устойчива, если лри каком-либо сильном возмущении сохраняется синхронная ра бота всех ее элементов. При исследовании устойчи вости необходимо определить. как поведет себи система в э1<стремальиых условиях и какие меры следует nрш1я1 ь, чтобы избежать и желательных nо следствий. Для выясне1-1ия nр11нциnиальных nо..'lожениН дннамвческой устойчнвост"1 рассмuгрнм явления, проходящие при внсза 1шом от ключении одной из двух параллельных цепей ЛЭП (рис. 11.11, а).
18' 275
Схемы замещения электропередачи в нормальном режиме при работе с двумя включенными цепями и в режиме с одной отключен ной цепью показаны на рис. 11.11, 6 и в соответственно. Резуль111- рующее сопротивление в нормальном режиме определяется выраже нием
х.,..1 х + Х..,,1 + х,/2 + Хтр2, а после откJ11011ения одной из цепей - выражением (11.19) $,
ll t Х рез2 = Х + Хтрl + Х л + Хтр2· (11.20) Рнс. 11.13. Устоi\чнвыА (а) н неустойчив ыА (6) режимы рвбслы системы
Так как Xdpe.;i.2 > Хdрез1. то справедливо соотношение Prnвx2 = E'Ucfx pcз9 <Pmзxl = E'VclX dpcsl·
(11.21)
Из (11.21) следует, что при неизменных Е', и. и изменении х;rез максимальное значение передаваемой ъющности меняется. При внезапном отключении одной из цепей ЛЭП ротор не успе nает нз-за инерции мгuовенно изменить угол б. Поэтому режим бу- дет характеризоваться ТО'IКОЙ Ь на дру
jJ_xк
i' Х и Uc р гой угловой характеристике генерато· а tf
LJ.-.\-...L.-'--.J..-...._..-5 личиваются. С увеличением угла мощ ность генератора возрастает по характе Рнс. 11.15. Схещ1 зн:.11щсю1я электропередачи для аиарнйно го режима (а) н ее nреобразов шш1 (6, в) "
Рассмотрим переходный процесс nри 1(3 одной из цепей ЛЭП с последующим ее отключением (рис. 11.14, а). Схемы замещения электропередачи для нормального и послеаварийного режимов по казаны соответственно на рис. 11.14, 6 и в. Угловая характеристика мощности ге;<ератора для нормального
откл1оченни одной ристике 2. В процессе ускорения ротор генера тора по инерции проходит точ1<у с, после которой его вращающий момент стано режима определяется выражением P1 =E'U,sin6/X 1, (11.22) где
вится оnережающю1-1. Ротор начинает затормажив аться и, начиная с точки d, ef'(J угловая с1шросrь уменьшаетсs1. При этом возника- 1от затухающие колебания вокруг нового устанониошеrося режима, сооrветствующего точке с. Если угловая скорость ротора возрастает до значения, соответствующего точке е или другим точна м на нис ходящей части характер11с111ки Р = f (б), то генератор выпадает Х1 = х,,.,,, = х + Хтрl + х,12 + ""•" а для лослеава риiiиоrо режима -выраженнем Pm = E'U,sinЬ!Xm, где Хш = Х роз2 = Х + Хт,1 + Х, + Хтр>.
(11.23) 113 синхронизма. Следовател ьно, ofi устойчивости системы можно судить по изме нению угла 6 во времени. Изменение 1>, nоказанн ое на рис. 11.13, а, соответствует устойчивой работе системы При изменении б по кри вой, изображенной на рис. 11.13, 6, система неустойчива. 27Р Схему замещения элект ропередачи д.пя аварийного режима можно получить, если в точку К3 включить шунтирующее сопро тивление х. (рис. 11.15, а), значение которого зависит от вида К3: х. = О при трехфазном 1(3; х. = Х, при двухфазном КЗ; Х. = - Ха +Хо при однофазном КЗ и Х. = Х 2Х 0/(Х, + Хо) при двух- 211
фазном КЗ на землю, где Х 0 и Х2 -суммарные сопротивления схемнулевой и обратноn последовательностей относительно точки КЗ. Схему замещения, показанную на рис. 11.16, а, можно последо вательно преобразовать из звезды (рис. 11.15, б) в треугольник (рис. 11.15, в), в котором х" =Х а + х" + X 0X.IX 0; }
Если при каrюм-либо значении угла боткл = бd поврежденная цель отключится, то в этот lУЮмент- nронзойдет нзм нение мощности генератора из точки с характеристики Ри (б) в точку d характеристи· ки Pm (б). Мощность же первичного двигателя генератора во время переходного процесса, ввиду инерr.uюнности системы регулиров а ния частоты враще1шя турбины, останется неизменной нравной Р 0. Пос11е отключения КЗ электромагнитная мощность генератора Хи = Хь-/- Х. + ХьХ.!Хи; XEu = х.+ х. + ХаХьiХк· (11.24) будет больше механической мощности турбины и на его валу nоявнт си тормозящий момент. Несмотря на это, ротор генератора еще некоторое время продолжает движение в сторону увеличения уг11а , Сопротивления ХЕ и Хи 1 подключенные нелосредствеиио к э. д. с. Е и к напряжению U0, на активную мощность генератора в вварий-11ом режиме суruестве1шо не влияют 11 могут не учитываться. При этом вся активная мощность генератора передается через сопротив ление ХЕи = _Х11, связывающее э. д. с. ге"ератора Е' с напрнже нием приемном системы U0, а угловая характеристика мощности ге- 11ератора определнется выражен11ем Ри = E'U 0 sinб/X11. (11.25)
амплитуды угловой характеристики мощ ности. Наиболее тяжелый аварийный режим будет при трехфазном КЗ в нача ле ЛЭП, когда сопротнw1ение XEu беско нечно велико, а амплитуда угловой ха рактеристики мощности равна нулю. Самый легкий авариnный режим соот ветствует однофазному КЗ, при котором б, лака не израсходуется запасенная им на пути от 60 доб.,,... кине тическая энергия. В этот период генератор покрывает избыток от· даваемой им элеитромаг111·1пюй мощвости за счет кинетической энер Рис. ll.16. rJювые характе. ристикн мощности генерато Ра дпя раэ11ых режимов сопротивление шунта КЗ будет макси Мальным. Угловые характеристики мощности генератора для нормального Р1 (б), ава у1·1ювую характерисп ну, причем после исчезновения возмущений еР параметры отличаются от первоначальных, но остаются в допусти Мых пределах. рийного Pu (б) и послеаварийного Р//1 (б) режимов показаны на рис. 11.16. Отдаваемая генератором мощность и угол между э. д. с. Е' и напряжением U0 в норма11ьнам ·режиме обозначены соот ветственно Р0 и 60. В начальный момент КЗ из-за инерции ротора генератора угол б мгновенно измениться не может. Это привuдит к внезапному уменьшению мощности от точки а на характеристике Р1 (6) Ю точки Ь на характеристике Рп (б). В результате на валу генератора возникает некоторый избыточный ускоряющий момент обусловленный разностью мощностей первичного двигат еля и гене: ратора, под влияuием которого ротор генератора 11ачи11ает переме щаться относительно вектора напряжения приемно системы (угол б увеличивается). Этому перемещенню соответствует увеличение мощности по характеристике Ри (б) в направлении к точке с. 11.4. Результирующая устойчивость Резулы·ирующая устойчивость характеризует способность систе мы самопроизвольно восстанавливать синхронную работу после кратковременного нарушения устойчивости. Приемной части системы. В асинхронном режиме генератор, кроме момента, обусповлеu ного его возбуждением, развивает еще и асинхронный момеит под действием свободных токов, которые возникают в его обмотке воз буждения 11 демrхрерных контурах из-за движения ротора по от1ю шению к поз1ю, созданйому внешними э. д. с. Наличие несимметрии генератора (явнополюсность, одноосность обмотки DОЗбуждения и т. д.) приводит к тому, что его асинхрон ная мощность пульсирует окмо некоторого среднего значения (рис. 11.17). Аналогично изменяются реактивная мощность и напря женне. Таким образом, асинхронный момент генератора может быть представлен в виде двух составляющих: среднего асинхронного мо мента и знако11еременного. Первый зависит от типа и конструкции генератора, а также от средН!'ГО скоJJьжения; второй не оказывает существенного влияния на протекание асинхронного режима и им о расчетах пренебрегают. Средний асинхронный момент генератора, подключенного не nосредствеflно к шинам неизменного напряжения, определяется вы ражением Мао= u; fsT (xd -х)/([1 + (sT)'I х.х) + + sT (x -x)/([I + (sT;)2]x x;) + + sт; (х.- х;)/(11 + (sт;)'J х.х;)}/2, (11.26) t 0,0G qов • Рис. 11.17. Лульсация асннхрон110А Рис. IJ.18. Зависимост;асин.хр0tшог<> мощности генератора момента rенератора и ero состввляю Ших от аюльжения которые обусловлены действием обмотки возбуждения (М). а так же демпферных продольной (М;) н поперечной (М) обмоток. Зависимость аснихроuного момента геиератора и его составляю щих от скольжения изображена на рис. 11.18. Видно, что наиболь ший вклад в Л1ас. вносит составляющая м;. Скольжения, соответствующие максимальным значейиям отдель ных составляющих асинхронflоrо момента, можно определить. если продифференцировать выражения sT I\ 1 + (sT)2 1, sT;/(1 +(s:т',;)2] и sт;111 + (sТ.)'1 по скольжению и приравнять производные к нулю. Тогда из равенства дМ /дs = (T [I +(sT }'j- sT. 2sТ ·и1 + (sT)21• =о находим s = 1/Т. (11.28) а из аналогичных равенств дМ;lдs = О и дЛ(,lдs = О получае,1 s = 11т; и s 11т;. Из (11.28) следует, ч1·0 чем больше постоянная времени контура, в котором находятся свободные токи. тем меньше скольжение, соаr ветствующее максимуму асинхронного момента. Прнмер 11.1. Для СЭС, схема хотарой изображена на рис. 11.19, а, оnределИ1Ъ коэффициент запаса статической устоilчивости no идеальному npeдeJIY мощности. Система состоит на ТИJtРОЭЛехтростанции (ГЭС) с геиераторгми GJ, 02 и ТЭС с эк4пвм:ентныw турбоrtнератороw: 03.. Параметры гидрогенераторов: Uном = 10,5 кВ, Р rl = Р г2 = 200 МВт. ,;:;os <i>гt = cos <rг2 = 0,85, xdl = xd 2 = 90 %, л: 1 = х 2 = 25 %; параметры по вышающих трансформаторов: К = 10,5/242, Sтpt = Sтр2 = 240 МВ ·А. ик1 = -= uК2 = 12 %; параметры ЛЭП: l = 300 км, хй = 0,41 Ом/км, Рп = 350 МВт. "COS <i>п = О,9; параметры понижающего трансформатора: К= 10,5/233, SтрЗ = = 1800МВ- А; Uкз = 14 %: параметры турбогенератора: ином3 = 10,5 кВ. р гЗ =
Активная мощность в относительных единицах, передаваемая по ЛЭП, Р. = Рл/Sо = 350/350 = l. Реактивная мощность при cos <vп = 0,9 (tg ЧJп = 0,485), передаваемая по ЛЭП. Q_. = р •Л lg ']Jл = l • 0,485 = 0,485. Полная мощность. передаваемая по ЛЭП, = 1500 МВт, cos <i>гз = 0,8, хdз = 180 %; параметры потребнтелеИ: Р11 = 1200 МВт, cos 'Рн = 0,8, Ии= 220 кВ. р е ш е п и е. Так юж мощность ТЭС значительно превышает мощность ГЭС, то можно принять. что генераторы GJ и G2 подключены к системе неоrрани ·ченно большой мощности и напряжение на шинах потребители постоянно (Uн = s.n = р •n +iQoл = l +j0,485. Для оnредс.'lения коэффициента запаса ста 'Тичес.кой устойчивости СЭС по идеальному пре делу мощности находим э. д. с. холостого хода генератора Таблица 11.2. Результаты расчета yrловой хара (тернстики мощности
= 220 кВ). При это;"11: условии схему замещения СЭС можно представить в виде, Eq = V< U +-Qл_x_dp-,-,l U J' + (=P x_d_p_" /U=) ' = б, град stn 6 р 0 0
 Tf ЛJIJ Tf ЛJIJ
а ,Рис. 11.19. К примеру 11.1 /f Zzf =Y(l+o,485- l,36tlJ'+(I · 1,36/1)'=2.15 н составляем уравнение угловой характеристики его мощности Р = EqU sin б/хdрсз = 2,15 • 1sin бtl,36 = = 1,58sinб.
о о 20 0,34 40 0,64 60 0,87 80 0,98 90 l о 0,537 l,02 l,37 l,56 l,58
показанном на рис. 11.19, 6. Принимая за базисную мощность Sб = 350 МВ • А, JJ за базисное напряжеине U6 = 220 кВ, приводим реактивные сопротивления се .элементов к базисным услониям н находим их результирующие значения: для генераторов
Идеальный предел мощности, соответствую щий в= go:i• Рmзх iJД = 2,15 • 1/1,36-== 1,58.
для повышающих трансформаторов Хтрl = Хтр2 = хтри омSб/(lООSНОМ) = = 12. 2422 • 350/(100. 240. 2202) = 0,212; для ЛЭП х, = xJSolU = 0,41 • 300. 3501220' = 0,89. Результирующее реактивное сопротивление СЭС xdpeo = (х,1 +х,Р1 + х,)/2 = (О,212 + l,бl +0,89)/2 = l,36. Внешнее реактивное сопротивление СЭС Хе= (х,"1 + x,;j/2 = (О,212 + 0,89)/2 = О,55. Лереходное реактиnнос сопротнвлсине генератора ГЭС х = х %U ONS1/(100SнmP) =
Результирующее переходное сопротнвл-ение СЭС х1 = х ре' = (0,45 -1- 0,212 -1- 0,89)/2 = 0,775. Напряжение на шинах потребителя в относительных единицах u0 = U/Uo = 220/220 = 1. Угол сдвига фаз между э. д. с. генераторов н напряжением на зажимах по т.ребителя б0 = arcsin (Р0/Рmзх liд) = arcsln (1/1,58) = 39°20'. Коэффициент заnа статическоii устойчивости СЭС по идеальному пределу t.ющностн к,= (l,58- l). 100/1=58 %.
.Контрольные вопросы
1. На какие группы подразделяются злектромеханиче<:кие переходные процессы? 2. Какие дuпущсния принимаются при анализе устойчивости СЭС? 3. Какие физические процессы описываются уравнениями электромехани ческих переходных процессов? 4. Какие схемы замещения синхронных генераторов используются в расче тю; устойчивостнi' 5. Как формулируется критерий статической устойчивости системы в обще:.r видеi' 6. С какой целью выполняется исследование статической устойчивости СЭС? 7. Как формулируются особенности исследования Шiнамической устой чивости СЭС прн разлиtIНЫХ видах КЗ? В. Какие отличительные признаки статической и динамической устойчиво сти СЭС? 9. Капой режим генератора называется асинхронным? 10. Что представляет собой асинхрQнный момент генератора? .282 283 Темы реферато• 1.. Осо6е1шос111 9J!ектромехs нических переходных реж11мов н шt плияш1е на Работу СЭС.
в 3. Отлнч1rrельные особенност11 ста-rнческой, дина.\1нческоn и результиру10- щей устсЖ•1нвост н СЭС.
ГJ1ава 12 ПРАКТИЧЕСКИЕ КРИТЕРИИ И l\IЕТОДЫ РАСЧЕТА 'СТОЙЧИВОСТИ СИСТЕ!\1 ЭЛЕКТРОСНАБЖЕНИЯ
12.1. Модели элементов при анализе Устойчивости Нений. В общем виде С.ЭС описываются системами дифференциальных урав1Jе1шй nысокого порядка. Дпя практических расчетов порядок системы уравнений обычно не превышает шести. При руч11ом счете можоо анализироват ь JJfJ деснт-и уравнений, а при ислользованин ЭВМ решаются системы уравнений более высоких порядков. Для оценки устойч иоости применяют J1инеаризацию систем диф· фсренциальных уравнений н нониженне их оорядка с целью п0J1у чення простых универсальных методон и алгоритмов расчета. В ли нейных системах уравнений н системах с несущественной нелиней ностью устой чивость анализируется методом малых колебан ий. Дт1 больших возмущений при а11ализе устойчивости используется вто рой метод Ляпунова или численное интегрирование. Понижение порядка систем уравнений, описыnающих исследуе мые процессы, может быть достигнуто их упрощением:
где Е.,, Eq1 -модули э. д. с. синхронных машин: Уи - модуль собственной эквивалентной проводимости; У<; - модуль взаимной sквивалентной проводимости между источниками; аи = n/2 - - arctg (xulr 11) и а11 = n/2 -arctg (xl/lrlf) - углы, характеризую щие соотношения между составляющими полных С твенных и взаим ных сопро11шле11ий электрической сети. Системы электроснабжения предприятий обычно подключаются к шинам центров питания, находящимся оод напряжением U. Урав Турбины совпадает по составляющим с урав нением (11.4) T,d2б/dt2 + М., = М, (12.8) Q = Px,sir, + U2 (1 - а+ aU')lxµ.
где Ммх - момент сопротивления рабочего механизма, и можеr нс пользооаться в расчетах кратковременных (до одного цикла кача 2
синхронных двигателей, которые электрически удалены от места а возмущения, сохраняют устойчивость и слабо влпяют на режим других маши н. Расчетная э. д. с. Е' включена за переходным сопро тполением двигателя х и определяется выражением [271 Е' = Jf U• - 2U'Qx + (Р' +([') x '!U, (12.9) где активная и реактивна< мощности двигателя ра эны: Р = E'U sinб/x; Q = (U2 -E'U соsб)/х. (12.JO) При расчете переходных нроцессов большой длительности сле дует иметь в виду, что переходные режимы генераторов характе ризуются ма11ыми скольжениями, тогда как скольжение синхронных двигателей может изменяться от ну.i1я до единицы. В этом случае нужно использовать уравне11ие движения сш1хронноrо двигателя T,d2бidt2 + p,,dб/dt = М - М "" (12.11) где p,jlб/dt - JJJt11еаризованный асинхронный момещ; Ра - коЭ<j, :рициент демпфирования, определяемый по линейной части асин хронной характеристнки синхронной машины как pd = dM!ds, а s = (ro0 - ro)/ro0 = dб/(ro.,dl) -скольжение двигателя. Электромеханический переходный процесс дл я асинхронного Та соответственно. Conpom в.ne1111e намагничивания можно рассчитать по форыуле Хµ = 1J{siп<p"0"-(I- V 1-4х соs2 <ри0.}/(2х.о)). Момент сопротивления для большинства вращающихся рабочих механизмов выражается зависимостью [24] м •• = м••.ст +(М••о-М••.от) ((1 -s)/(I -s"0.))", (12.16) rде Мм t.ст - начальный (статический, ro = О) момент сопротивле яия; Ммхо - номинальный момент сопротивления механизма; р - показатель степени, зависящий от типа оборудования [27]. В уравнениях движения элементы электрической сети (узлы, ветви из ЛЭП, трансформаторов и т. n.) описываются по-разному. Для узла сети с п ветвями должен выполняться баланс активных 11 реактивных мощностей: n Вид уравнений движения нагрузки зав11сит от прин11ыаеыой расчетной модели ее узла -группы разнородных злектроnрие м ников, присоединенных к узловой точке сети. Расчетная модель нагруз1<и предприятия определяется составом потребителей и его распределительной сетыо. В общем случае она ыногоэлементная, где каждый узел нагрузки содержит матемll'l'иЧес1юе описание экви· валентных параметров асинхронного и синхронного двигателей. а также статической нагрузки zн (освещение, выпрямители, инвер торы. электропечи, нагревательные приборы, коммунально-бытовые электроnриемиики, конденсаторные батареи и т. п.). В математическом олнсании р асчетной модели нагрузки исrюль зуют статшш:кие и динамические характеристики. Они представ· ляют собой зависим.ости патребляемой yЗJJoM нагрузю1 активной и реактивной мощностей, вращающего момента или тока от напряже ния и частоты. Статические хара1сrеристики нагрузки Р" F, (U, w); Q" = F, (U, w) (12.19) определяют вариации Р н• Q" при медленных изменениях напряже ния и угловой скорости. Задание нагрузок в
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.168.40 (0.013 с.) |


 Q P,Q
Q P,Q
 Таблица /1_/. Выражение вели•1ин, входящих а уравнение (11.1)
Таблица /1_/. Выражение вели•1ин, входящих а уравнение (11.1) (P,-1'"J <»о= Т1 (d'бldt')
(P,-1'"J <»о= Т1 (d'бldt')

 возрастает.
возрастает.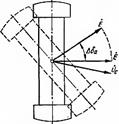





 180
180