Следовательно no интервалам.

чаемому по (12.83) пр ельиому углу отключения. Для 11роизволь-

1юrо момента времени связь этих величин отражается уравнением движения (11.4). Аналитическое решение ero возможно только для частноrо случа я, а именно полиоrо разрыва связи генератора с ши­ нами приемноr1 системы, когда Р = Р 11 (6) = О, что пронсход>п

В каждом интервале времени из­

быток мощности (правая часть

уравнения) считают неизменным

и при ЭТО}! допущении вычи.сля­

ют прираще11ие угла д6.

Pl!c. 12. 13. К расчету динамической устоnчивостн системы методом пос.1е­ довательных: ннтерваJюв

11ри трехф•зном КЗ на одной иs цепей ЛЭП. При этом ураяиение

(11.4) упрощается и nрииимае·r BИJI

В момент сброса мощности (момент КЗ) возникает избыток мощ­

ности дРu (рис. 12.13). Приращение угла в течение первого интер­

вала времени Лt находят при начальных условиях (d&/df)1-o = О

Т1 (d2/'J/dl2) = Р0. (12.84)

и (j = ()0

последовательным интегрированием уравнения (11.4):

Решение этого уравнения методом последова.r ельного интегри­ рования при постоянных с1 = (dбldf),o={! = О и с, = ()0 позволяет

М Л12ЛРоf(2Т,); б1 = 6о + М,. (12.89)

311

 

Во втором интервале времени ротор генератора движется под действием избытка мощности ЛР1 = Р0 - Pт:i-y,lf sinб1и некоторой начальной скорости. приобретенной в первом интервале:

(dб/dl)1 = лt (ЛР0 + ЛР1)/(2Т,). (12.90)

Решив уравнение (11.4) относительно приращения угла во вто­ ром интервале времени, получим

М2 = Лt2ЛР1/(2Т,) + Лt (dб/dt),. (12.9!)

После преобразования (12.91) с учетом (12.89) и (12.90) найлем

Лб2 = Лб1 +Лt2ЛР1/Т,. (12.92)

Если постоянную инерции т, и время Л1 выразить в секундах, уг."ы ЛЬ, и ЛЬ2 - в градусах и ввести постоянную

k = 18 ооолt21т,,

то выражение (12.92) примет вид

 

ii.r/н:rrJJI 1(Zrp2 zfl.z f;:

 

 

z

Рис. 12.14. Схем.а электрической сисrемы с двумя станциями (а) и схемы ее за

мещсния.в нормальном (6), аварийном (в) и nосле шарийном (г) режимах

 

В схемы замещения системы для различных режимов введем· модель нагрузки в виде неизменных комплексных сопротивлений_ При этом связь между источниками электрической энергии созда

Лб2 = Лб1+ kЛР,.

д;я п-го интервала времени по аналогии запишем

(12.93)

ется пассивными элементами и ее можно выразить через собсrвен· ные и взаимные проводимости ветвей с учетом сопротивлений на­

грузки. Тогда угловые характеристики мощности генераторов стан­

Лбп = Лбп-1 + kЛPn-1· (12.94)

Если в i-м интервале времени происходит изменение режима о переходом из одной угловой характернстнкн мощности на друrую (см. рис. 12.13), то приращение угла определяется выражением

ций на основании уравиеиня (12.2) примут вид

Р1 = Е!Е у 11 s na11 + Е Е у12 s n (1\12 -а12); }

Р2 = Е2Е2у22 sша22 - Е1Е2у 12 sш (б12 +а12). •

 

 

02.91r

М1 = ЛI\,_, -1- 0.5k (ЛР;_, +ЛР;_ 1). <_\2.9:>)

Расчет точек кривой 1\ = f' (пЛ() следует выполнять до тех пор, пока угол Ь не начнет уменьшаться по кривой 1 (см. рис. 12.13), что соответствует сохранению устойчивосrи, или пока не будет установлено, что угол б продолжает возрастаТь по кривой 2, ссхн­

ветствующей нарушению устойчивос-rн. По кривой Ь = f (() можно

определить также предельное времи отключения КЗ, используя

вычисленное по (12.83) значение предельного угла отключения.по­

врежденной цепи ЛЭП.

Схемы замещения системы для нормального, аварийного (КЗ)• и послеаварийного (отключение ЛЭП) режимов показаны иа

 

р Otz l1t1:::VJ{Df2)

A.v<,

 

 

12.5. Оценка динамической устойчивости сложной системы

 

Обычно СЭС предприятия получает питание от несколькнх. не­ зависимых источников. В этом случае систему внешнего элекiро­ снабжеиия можно рассматривать как сложную систему. Наибрлее распространенной является СЭС с двусторонним питанием.

Рассмотрим электрическую систему, содержащую две ста' ции, элементы связи межДу иими и нагрузки (рис. 12.14, а). Работа ге­ нераторов станций описывается уравнениями

 

 

о

Рис. 12.15. Зависимость мощности и относитыыюго уск()рения р()торGВ генера­ торов станций от взаимного угла перемещения роторов

 

рис. 12.14, 6-г. Они содержат неизменную во всех режимах э. д. с. станций и переменные при смене режимов проводим.ости ветвей между ними. Угловые характеристики мощности с у\1етом направления ее передачи от станций в сеть для рассматриваемых режимов изображены иа рис. 12.15, а; они построены для общей

Tлd21\1/dt 2 = Р10 -Р, = ЛР,; }

переменной -взаимного угла 612

перемещения роторов генерато­

Tпd21\ /dt 2 = Р

-Р = ЛР • (l2.96)

ров станций.

2 20 2 2

312 313

В момент КЗ происходит измеиеиие отбираемой от генер аторов

:активной мощности и рабочие точки генераторов перемещают ся из

<1 и а' соответственно в Ь 1Г Ь'. В даноом случае ротор генератора первой станции будет ускоряться под действием избытка мощнос­ ти др\"' > О, а ротор генератора второй станции замед11яться под

.действием избытка мощмости ЛР"' < О.

Соотношение и знаки избыточных моментов зависят от парам:ет ров системы, вида возмущающего воздействия и рассматриваемого v.юмента времени. Выполнить оценку динамической устойчивости

<110 значениям избытков ыощности и приршцениям углов для каж­

.дого генератора невозможно, так как при этом неизвестен знак ск<r

рости относительного перемещения роторов генераторов станций (зиак скорости изменения взаимного угла 1\12). Учесть этот знак

\IОЖ/Ю по второй производной этой переменоой -отиосительиому

:ускорению роторов генераторов станций.

Для этого уравнения (12.96) нужно привести к i!иду

d'l!1/dt' = ЛР1/ТJt; \ (12.98)

d'б.fdt' = ЛРJТ". f

l'азность между уравнениями (12.98) позволяет пОJJучить уравнение

<Jтиосиtельного движения роторов генераторов станций

- а;2 = d'б,.2/dl' = ЛP1!TJt -ЛP2/T Jz. (12.99)

•·де а12 -относительное ускорени" роторов генераторов станций.

Из зависm.юсти au = tp (б") (рис_ 12.15, б) следует, что уско­

а"

f>ение это знакопеременное_ Так как между относительными уско­

.реиием и скоростью перемещения роторов v11 существует связь

 

б"

Равенству } а1,,dб11 = О соответствует скорость v" = о. что

бt2(0)

вьшолияется при Ау" =А..,,. (см. рис. 12.15, б). Наибольшая площадь торможения

a12tn>

л;,,," = S а"dб"

Ot2(m)

мткет быть исrю.льзоваиа для оценки запаса динамической устой­

ч нюсти К з = Атор м!Ауа< сисrемы.

При сыене режимов работы СЭС характеристики относительного

};/к ения роторов генераторов ста ий строят для аварийного

а" - '1'11 (б1.) и послеавариiшого а12 = tрш (бiz) режимов (см.рис. 12.15, в). При этом из-за отключения повреждения рабочая точка режима перемещается нз с в d. На графике можно выделить площади ускорения и торможения. Их равенство соответствует предельному значени ю угла отключения КЗ б12откл.поед·

Предельное время отключения КЗ, соответствующее углу б,,,,.,.." nоед• находят по зависимости 1\11 = f (1), которую строяr меrодом последовательных интервалов. Основные этапы ее расчета

такие же, как и для системы с одним генератором, работающим на шииы неиэмеиоого напряжения (см. п. 12.4). Дополнител ьно для каждРrо интервала определяют приращение взаимного угла перемещения роторов.

В первом интервале (верхний индекс в скобках озиачаеr номер интервала) имеем

й13 = dv12fdl. (12. 100)

-то при положительных значениях ускорения относительная ско·

рость перемещения роторов зрастает, а при отрица1'Е'Льиых зна·

б\') = ь,1°' + ль:•); б ') = бl(°' + лt:JГ;

льШ = ль/'' -л&');

(12.102)

(12.103)

С еннях - уменьшает ся.

.v,,

После преобразования выражения (12. JOO) с учетом того, что

= dб,_.,ldt, получим

а,1= (dv12/dб13) (dб12/df) '*а12dб12 = v 12dv11•

Интеrрирооат1е последнего тождества дает

Otl V11 V1 1

} а"dб12 = } v12dv,, = 0,5v2 j = 0.5v2• (12.101)

012(0} t'12(0) =0 о

ь\ = ь.2(0) +ль: = ьl'' - &]'. 02.104)

Во втором интервале по (12.96) и (12.97) рассчитьmают избытки

•ющносi)" в нача е ""J. вал а (конце первого интервала) д.я пер-

110 llP\ и второи ЛР, станций, а также приращения углов:

ль:" = ЛЬ!" +k,ЛР:') при k, = 18OOOЛ/2/TJt;

Лf!..,, = llf!.1 +k,лр1,,'! при k. = 18 ОООЛ/2/Т J2,

откуда пОJJучают

л& = мf + k,ЛР\'' -k л111;

Левая часть равенства (12.101) определяет площадь, которая ()граннчивается кривой а.,, = tp (б1.) (см. рис. 12.15, б). Эта пло­

ь: = ь\

2)

+ ль\.

щадь пропорционал.ьи а скорости относительного перемещения ро­

·торов генераторов. Соответствеиио эиаку относительного ускорения

можно выделить площади ускорения (увеличение скорости отио­

-сительного перемещения роторов) и торможения (ее уменьшение)

.и использовать метод площадей на основе равенства (12.101) для

()1Jенки устойчиnостп системы.

Для последующих интервалов приращени>J углов вычисляют

110 аналогичным формулам:

ль:"' = Лбjп-1) +k,др:•-1); льr) = щп-11 + k,l\Pif' -'';

М\"1 = мr.-11 + k,ЛР\"-" -k лpt-•):

б!';' = ь -·· +Лбf;'.

.з14

 

Дш амическую устойчивость СЭС с ч11слом источников более двух аиапизируют в осиовиом методом последов ательных интерва­ лов в изложенной выше последовательности. Такие системы mно­ сят к сложным н они характеризуюгся совокупностью независимых перемен ных взаимных углов между парами роторов генераторов. Наличие болы.uого ч11сла независимых переменных не позволяет воспольэоваты:я методом шющадей для опрl\делення предельного угла отключения КЗ; поэтому метод последовательных интервалов используют для расчета конкретного, заранее заданного времени отключения КЗ.

В каждом юпервале приращения абсолютных значений углов

6 перемещения ротора каждого генератора вычисляют по форму­

лам (12.102). Избытки мошности по каждому исrочнику удобно

 

rs 4s

 

При увеличении передаваемой в сеть мощности по сравнению с исходным режимом (11 > /0) одновремеиио увеличивается угол 6, а. вектор э. д. с. Ец0 генератора меняет направ.nение при 1F..,1 =

= 1Ец0 1 (рис. 12.17, а). При этом иапряжение на зажимах гене­ ратора уменьшается (iJ,, < U,o). Сnедовательно, прl\дел мощнос­ т11 (12.105) при 6 = n/2 снижается.

Г:сли генератор имеет АРВ, то увеличение передаваемой мощ·

ности н связаноое с ним увеличение угла 6 приводят к изме11е1шю

э. д с. генератора. Эго соответсrвует nереходу с угловой характеристики, nocтpoeuнoii прн постоянной э. д. с.

ly, Ец0, на угловую характеристику, ко-

торая соответствует nостоянной э. д. с. Б., > Е.о (рис. 12.17, б). С возраста­ нием угла б э. д. с. генератора меня­ ется, а согласно характеристике пе-

 

р

11

Рнс. 12. 16. Характер 11зменения взаи\шых уrдов nеремещениn роторов re·

нер.нторов для снсте:.1ы с тремя источниквми nрн <.:охранении (а) н наруше· о

н111:1 (6) ее устоnчивости

 

определить, используя уравнения типа (12.96) и (12.97). Для каж­ дого интервала по абсолютным значею1нм углов 6 находят µаим­ ные углы между парами генераторов 13\ >, б, Щ!},..., б), приме­ няя формулы типа (12.103) и (12.104) для nосtроения зависимосrей 6,, (1), 6" (t), 6" (f), "., 6" (t).

03 устойчивости СЭС судят по характеру изменения взаИ\IНЫХ

углов. Их изменение во времени должно быть единообразным и невозрастающим (рис. 12.16, а). Признаком пеустойчнnости СЭС является монотонно возрастающий характер части зависимостей

взаимных углов от времени (рис. 12.16, 6).

Характер изменения зависимостей б" (f) определяю·r для каж­ дого заранее заданного времени отключения КЗ. Чтобы установить предельное время отключения КЗ, изложенную nоследоватеды1ость расчетов необходимо повторить для дру•·их значений времени от­ клю•<ения 1(3, пока ие будет установлен характер изменения зави­ симостей 11" (f), подтверждающий устойчивость или иеусrойчивость СЭС.

 

12.6. Учет автомати ескоrо реrулирования возбуждения при расчете устойчивости

по виутревиему пределу мощности

 

Угловая характеристика мощности генера тора без АРВ пр11 постоянной э. д. с. Ео0 определяется выражением

Р = Ец0И siпb/(xd +х,"). (12.105)

 

Р11с. 12.17. К рассмо­ трению uлпянин АРВ генератора на парамет-

ры режш.tа СЭС S

 

редавае юй в сеть мощности преде.л мощности повышается, харак­

теризуя сь смещением в зону углов 6 > n/2. Таким образом, АРВ

влияет а предел передаваемой в сеть мощности и, следовательно. на устойчивость еэс.

При рас•1ете устойчивости важное значение имеет учет типа уст­ роikтв АРВ. Различают автоматические регуляторы пропорцио­ "ального типа и автоматические регул яторы сильного деikтвия_ Первые реагируют на отклонение одного или нескольких парамет­ ров режима от контролируемых значений, вторые дополнительно реагируют на скорости н ускорения изменеиия параметров режима. Введение 11роизnод11ых иэ:ме11е11ия.параметров режима в законы регулирования не только стабилизирует систему регулироuа1шя, но и значительно повышает предельную передаваемую мощность (предел устойчивости). Автоматически е регуляторы пропорцио­ налыюrо типа обеспечивают устойчивость режима в меньшем диа- 11азо11е изменения угла 6 и передаваемой ющности Р (кривая 2 на рис. 12.17, в) по сравнению с автоматичес1шми регуляторами сильного действия (кривая 3 на рнс. 12.17, в). Кривая J на рис. 12.17, в хврактеризует угловую характеристику мощности генератора без АРБ.

 

:Jl7

 

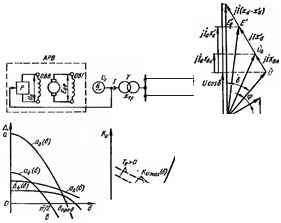
Рассмотрим, как учитывают АРВ генератора при расчете устойчивости СЭС уточненным методРм с испОJJьзоваиием 11рактнче­ ских критериев. Ощ,нка пределов устойчивости СЭС без АРВ гене­ ратора н с АРВ может быть сведена к ощ,нке предельной мощности, передаваемой генератором в сеть.

Оценка статическоi! устойчивости. Выполним анализ стати•rс· екай устойчивости простейшей электрической системы с генерато- ром, оснащенным автоматическим регулято· i.

ром пропорционального типа по отклонению,• напряжения и работающим на шины с иеиз- il;JX1

меиным напряжением (рис. 12.18, а). Переход­ ный процесс здесь можно описать системой уравнений, включающей в себя:

 

 

/1911

 

;

 

иР -

шемся режиме, равная в относительных единицах напряжении:> возбуJ1.11теля; Т, - оостоянная времени обмотки возбуждения воз­ будителя (ОВВ); устаоовившееся значение напряжения ОВВ. равное в отоосиrелы1ых единицах напряжению на выходе регуля­ тора.

Уравнение идеаnьноrо автоматического регулятора напряже·

ния пропорционального типа, мгновенно изменяющего напряжение­ на ОВВ, пропорционально отклонению напряжения на зажимах генератора:

(12.109)>

где Ки -коэффициент усиления (регулирования) регулятора.

Система уравнений (12.106) -(12.109) содержит шесть пере­

менных: б, Eq, Е;, Еqг, Up, Ur. Дополнительные уравиеиия связывающие их между собой, могут быть получены из векторною диаграммы генератора (рис. 12.18, 6):

E.=иcosб+ldXd; (12.110)>

Е =исоs6+1.х; (12.111, а;

;,

z_. (/JЛ.Sf

 

Q

......'-----

 

где

и. и"= и соsб + 1.х... (12. J\2, a)i

 

х •• =х.,,+О,5х.; х.=х.+х ••; Х =х +х ••.

" 4t

W60ml•;:

Т,=О 40

=.m"*,m-1-- 20

'---.,,... т---11" 8 f 2.J 4 r,,c

tl

Определив из (12.110) ток Jd и подставив его в уравнения· (12.111, а) и (12.112, а), запишем недостающие уравнения

в = в.х 1х. +иcos6(X.-X)/X 4; (12.111, б)-

и,= в.х...1х.+ иcasll(Xd-X ••)fXd. (12.112, б)о

Систему уравнений (12.106) -(12.109), (12.111, б) и (12.112, б) представим через соответствующие линеаризованные уравне11ия составленные иа основании малых приращений. В операторной • форме записи они имеют вид

Рис. 12.18. К анализу стап1ческой устойчивости элехтрической системы с нвто· матическим регулятором пропорцнонального типа по отклонению наnряжсння

уравнение относительного двнж?иия ротора генератора

(Т,(w)d'6/dt• = Р - E.V sinl'Jfx.; (12.106)

Д/j (TJ!Wo) р2 = Л6дР/д6-ЛЕqдР!дЕ 0;

ЛЕ Т•оР + ЛЕ 0 = ЛЕ";

лЕ•.(1+ рТ,) = ли0;

(12.J\3)

(12.114)

(12.115)

0 0

ли =-КиЛи,;

(12.116)

уравнение переходного процесса в роторе генератора (контур цепи возбуждения генератора с независимым возбуЖдением)

TaodE!dt -f Е• = Е"; (12.1<J7)

уравнение переходного процесса в цепи возбуждения возбу­

дителя

T,dE"!dt+E" =иp. (12.108)

Величины, входящие в урав11ення (12.106) -(12.108), озна·

чаЮ'Т: Т•о -IЮСТОя1111ая времени оомоткн возбуждения генерато­

0

ЛЕ = Л6дЕ!д6 + ЛЕ,,дЕ /i!Е.;

ли. = Л6дU,/д6 + ЛЕ.ди,tдЕ ••

где частные производные переменных

дР!,дЬ = SEQ = в.и_соs6/Х4; дР/д · = иsin.13/X.;

дЕq/д/j

= иsiпll(X.-Xd)!Xd; дЕq/дЕq = х.1х.; ди.fд/j = иsinll(X", -Х.)!Х.; ди,!дЕQ = х_1х •.

 

(12.117)

(12.ll8);

 

 

(12.119)·

Е., -

ра (OBI) при разомкнутой об'ютке статора; Е и Е0 - переход· ная и синхронная продольные э. д. с.; э. д. с. в. установив-

 

Для получения хар11ктеристическоrо уравнения системы·

(12.113) -(12.118) необходимо выполнить следующие nреобразо-

319'

JЗания: (12.118) подставить в (12.116), а полученное значение ЛUр -

,; (12.115); значение ЛЕ" из полученного уравнения, а также

{12.117) подсrавить в (12.114); для полученного уравнения н

 

Л.ля выявления условий устойчивости системы можно восполь­

зоваться критерием Гурвнпа (см. 11. 12.3):

{12.113) составить определитель системы и раскрыть его. В резуль­ тате характернсгнческое уравнение примет вид

а0р• +llif'3 +(а2 + КuЛ.)р2 +а,р + а4 + КиЛ 4 =О, (12.120)

а,+ КuЛ,>0;

а3 >0;

а,+ КиЛ4 >0;

(12.122)

(12.123)

(12.124)

)<'Де

 

а0 = (T,/ro.) т,.тjJE;lдE.; а,= (T,fro.) (Т,0дЕ;/дЕ. + Т,);

а, (а, + KuЛ2)a,-af (а4 + КиЛ 4)-а.а >0. (12.125)

С целью упрощения анализа условий устойчивости вначале

а2 = T,/(jj0 + Т,оТ,[(дЕ;tдЕ•) (дР/дl:J)- (дЕ;/дl:!) (дР!дЕ.)]:

поJJагают, что постоянная времени возбудителя

Т, = О.

Это

по­

 

а, Tdo [(дЕ!дЕ,) (дР/дl:J)- (дЕ;/дб) (дР/дЕ.)]: а4 = дР!дб;

Л2 = (T,iw0) (дU,!дЕ,); Л4 = (дР/дб) (дU,!дЕ.)- (дР!дЕ.) (дU,!дб).