Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ветст.зу1сщим коэффициентам характеристического уравнения, про-Содержание книги
Поиск на нашем сайте
1101щиональные коэффициенту усиления регулятора). Анадизируя (12.121), можно сделать следующие выводы: тшэффшtиенты а0 н а1 всегда положительны и не зависят от ре жима работы н параметров сеш, па которую работает генератор: коэффициеmы а2, а3, Л4 н а4 зависнт аг режима работы и пара метров сети. С увеличением угла б некоторые из них становятся vтрнцательнымн (рис. 12.18,. в), что свидетельствует о нарушении необходимого условия устойчивости системы, соответствующего 1юJюжительным значениям всех коэффициентов характеристиче -с1юго уравнения.
те.пьное значение при углах, ббльших п/2, и тем самым устранить причину нарушения устойчивости нерегулируемого генератора. Условие наличия положительного знака у коэффициента а4 опре деляет границу иаимеиьших значений коэффициента усиления по mклонеиию напряжения, что следует из (12.124):
 (12.. 126) (12.. 126)
Характер изменения зависимости К.и m;n (б) показан на рис. 12.18, г. При положительном коэффициенте а4 устойчивосrь может нарушиться при изменении знака ·"ибо у коэффициента а, (наJ1нчие регулирова11ия по отклонению напряжения на него не влияет), либо у неравенсrва (12.125).
21 8-3'755 321 (12.111, б), то получим Р = E U sin6/X -U2 sinl>cosl>(Xd- x;)/(XdX). или Р= E Usinl>IX.-U 2 sin26(X.- Х)/(2Х•Х). (12.127) Частная производная при Е = const имеет в щ дР/дЬ = sЕ = Ер cos 1>1х - и• cos 21> (Х.- X >t<x.x >- c учетом (12.111, б) и равенства cos21> = соs2б -sin26 имеем SE = E,JJ cosl>/X• + U'sin2 l>(X.-X)/(X•X). Если учесть также (12.119), то получим
условие по критершо Гурвица (12.122)-(12.125). Неравенство (12.122) не определяет устойчивость системы, nоскольку оно нару шается всегда позже неравенства (12.123). что очевидно из (12.121). Из сопоставления неравенств (12.123) и (12.124) следует, что раньше нарушается неравенство (12.123): при Т, = О и 1> = l>npeд оба неравенства нарушаются одновременно, а при Т, >О увеличи· ваются значения Ku, что обеспечивает соблюдение неравенства (12.124) при больших углах 6. Таким образом, граничное условие устойчивости системы определяется неравенствами (12.123) и (12.125). Из неравенства (12.125) следует, ч,то максимальное значение коэффициента усиле ния регу"1ятора определяется выражением
SE = sE. +и• sin2 6(X.-X)/(X.X). (12.128) При уве 1ичении IЮСТОJIННОЙ времени возбудителя Ки max так Из сопоставления (12.128) с выражением а8 в (12.121) следует, что при Т, =О а3 = T SE. Таким образом, знак у коэффициента же возрастает (рис. 12.18, д). С увеличением угла 1> значения Ки rna' вследствие уменьшения коэффициента 0з [см. (12.121)1 падают. При а3 =О коэффициент усиленияКиmа:х = аiЛ4, что меньше его а q в;· 8 определяется знаком синхронизирующей мощности S Анализируя (12.125) с учетом (12.121). находим максимальное значение коэффициента усиления регулятора Ки mвх = Х,!(Х •• (1 - x4X.t((x.- х) Х."))), а интерва"1 изменения этого коэффициента следующий: -а4/Л4 < Ки <(а1а4 -а2а8)(а1Л4 -Л2а3). (12.129) Рис. 12.18, г показывает, что устойчивость снеrемы нарушается при углах 6 > бnред, лежащих вне выделенной на нем области. Для 1> = linpeд после преобразования (12.129) 11u,1учаем а (Л а - а2Л) =О, значения при Т, =О!см. (12.129)1. Поэтому при возрастании угла 1> и Т, >О первым нарушается условие устойчивости (12.125). которое является граничным для установления предела мощности по статической устойчивости системы с автоматичес1mм регулятором пропорционального типа по отклонению напряжения. При АРБ генератора по отклонению напряжения с заданным коэф:jшциентом усиления регулятора предел статической усгой· чивости системы рассчитывают в следующем порядке: 1. Определяют значение э. д. с. в установившемся режиме Е.=Е.о+Ки(И.о-Иг). (12.131) где Er;o и Uго -соответственно э. д. с. за синхронным индук· тивным сопротивлением и напряжение на зажимах генератора в 3 2 4 4 исходном режиме. а если учесть (12.121) при Т, = О, то последнее равенство можно записать так: SE (TДJro0)U2 sin2 1iX•• (Х. Х••)/Х =О.
Следовательно, при /(u of:. О и 1> = l>npeд синхронизирующая мощность еще положительна. Эго позволяет сделать вывод о том. что граничным условием нарушения устойчивости системы с авто матическим регулятором пропорuионалыюrо типа по отклонению напряжения является условиеSЕr; =О. Кроме того, введение такого
висит от коэффициента усиления регулятора. При постоянной времени возбудителя Т, > О оценка условий уст<>йчивости системы состоит в следующем. Выделяют граничное 2. Подставив значение (12.112, б) в уравнение (12.131). нахо д>1т значение синхронной э. д. с. 110 формуле Е. = lE.o+ Ки(Игv-U cosl>(X.-X••)}IX.1/(1 + . + KuX ••tX.). (12.132) 3. Вычисляют по формуле (12.111, б) значение переходноi1 э. д. с. 4. Преобразуя уравнение (12.105) с учетом (12.132), получаю угловую характеристику мощности Р= l(Equ + KuИгo)Usinl\-U"l(u(X•-X•.) х х sin2б/(2X.))/(X.+KиX"). (12.133) С достаточной дл>1 практических расчетов точностью угловую ха рактеристику мощности можно определить также по формуле (12.127), используя найденное "" (12.111. б) значение синхронной э. д. с. В22 21• З2З 5. Находят предел передаваемой мощности и предельное зна чение угла перемещеиия ротора генератора. При использовании угловой характеристики мощности (12.133) предел передаваемой мощности определяют rю предельному значению угла бnреА• полу чаемому из решения уравнения (12.130), которое приравнивают зада11ному значению кОЭФРициента усиления, и вычисляют значе ния коэффиuие1tГОв по (12.121), а сиихроиную э. ц. с. по (12.132): с, cos• блоод + с, cos 1\лред + с3 = О и бnред = arccos 1\nред. (12.134)
возбудителя, то прн форсировке возбуждения закон ее нарастания Можно за писать в виде Е" = Еqеф = Eq«J +(Е., rnax -E.")fl -ехр(-1/Т,)], lмп < <1<11• (12.135,а) Форсировка возбуждения продолжается до достижения 11а11ря· жения генератора (0,95 7 1,05) Uг.но•· При снятии форснроnк11 напряжение возбуднтедя и э. д. с. генератора уменьшаются 1ю где с,= ll'[Ku(Ta + T,)(Xd-X ••y(Xd(X. + Х.нКи)) + + Td(Xd- X)/(XdX)]; с, = - U (Т + Т,) (Eq0 + KuUгo)!(X. + х."Ки): закону
rде
с, = - U'T (Xd -X)/(XdX) + Т,(Т + T,)i(T w0 Х х ((1 + Т.(Х.-Х••)Х!(Т (Х -Х••)Х.)) х х (Х -Х,")Ки/(Ха-Х,.)-1)). 6. При испоJJьзовании угловой характеристики мощиоеrи (12.127) предельное значение угла бпрец можно найти из уравнения (12.128), iюлагая SЕ' = О. Зная закон изменения э. д. с. генератора можно методом nоследовательных интервалов чис .n
магнитного переходного проuесса в роторе генератора Т.rodE!dl +.Е. = E.,(t)
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.180 (0.012 с.) |

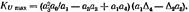
 Е., = Е"Ф-(Е"-Е,,.о)[l -ехр(-1/Т,)], t>t" (12.135,б)
Е., = Е"Ф-(Е"-Е,,.о)[l -ехр(-1/Т,)], t>t" (12.135,б)