Тические описания синхронных и асинхронных машин. элементов

сети н узлов нагрузки.

Упрощенное уравнение движения синхронной машины (генера­

тора, компенсатора) может использоваться в виде (11.4), где элект­

рическая (внутренняя) мощность одиночной машины

Р = Е (t) / (t) cos <р (t). (12.1)

Здесь Е (t) - лннеf1ная э. д. с. машины; / (t) -ток в обмотке ее

статора.

Для электриче ской системы, которая содержит 11е одну машину,

при определении внутренней мощности необходимо учитывать влия­ ние других машин через их э. д. с. и взаимные углы положения ро- 1·оров б,1 = б1 - б1. Уравнение внутренней мощно= i-й синхрон­ной машины, которая работает параллельно с 11 - 1 другими син­

Хронными машинами, имеет вид

п

Мате:матиt1еское олисание СЭС для иссJ1едования их устойчи­

вости основывается на теории дифференциальных уравнений. Прн этом анализ устойчивости режимов реальных еэс сводится к иссле­

Р, = E,y"sinaa + E.,E.;Y11sin(бц- а11).

i=l

/#

(12.2)

дованию устойчивости решений систем дифференциальных урав­

Нений.

В общем виде С.ЭС описываются системами дифференциальных урав1Jе1шй nысокого порядка. Дпя практических расчетов порядок системы уравнений обычно не превышает шести. При руч11ом счете можоо анализироват ь JJfJ деснт-и уравнений, а при ислользованин

ЭВМ решаются системы уравнений более высоких порядков.

Для оценки устойч иоости применяют J1инеаризацию систем диф·

фсренциальных уравнений н нониженне их оорядка с целью п0J1у­

чення простых универсальных методон и алгоритмов расчета. В ли­ нейных системах уравнений н системах с несущественной нелиней­

ностью устой чивость анализируется методом малых колебан ий. Дт1 больших возмущений при а11ализе устойчивости используется вто­ рой метод Ляпунова или численное интегрирование.

Понижение порядка систем уравнений, описыnающих исследуе­ мые процессы, может быть достигнуто их упрощением:

.

разделением процессов на быстрые и медленные с обособлеииым

где Е.,, Eq1 -модули э. д. с. синхронных машин: Уи - модуль собственной эквивалентной проводимости; У<; - модуль взаимной sквивалентной проводимости между источниками; аи = n/2 -

- arctg (xulr 11) и а11 = n/2 -arctg (xl/lrlf) - углы, характеризую­ щие соотношения между составляющими полных С твенных и взаим ных сопро11шле11ий электрической сети.

Системы электроснабжения предприятий обычно подключаются к шинам центров питания, находящимся оод напряжением U. Урав­

Нения внутренни1' активной и реактив 11оi'1 мощностей сипхропиоrо

Генератора в этом сд учае имеют вид

Р = E ysina +Epy sin(б-a); (12.3)

Q = Е усоsа-Ерусо,(б-а), (12.4)

где у -модуль проводимости сети между источником и шинами

ээс.

Эти же мощности на шинах ЭЭС описываются выражениими

их рассмотрением;

заменой групп источников или двигателей одним эквивалентным;

предеrавJJением нагрузки обобщенными характеристиками;

выделением существенных факторов в протекающих процессах '

Р' =-U•ysina + Epysin(б +а);

(( = -U•ycosa + Epycos(f> +а).

 

02.5)

(12.6)

и пренебрежением второстепенными факторами и малыми парамет­ рами;

линеаризацией характеристик ЭJJементов СЭС;

разделением сложной системы на простые оодсистемы, которые

можно рассматривать независимо.

Трудоемкост ь решения задачи устойчивости зависит также от уровня аналитиче ского описания математических моделей основных элементов СЭС. Для решения задач устойчиво сти применительно к СЭС промышленных предприятий приемлемы упрощенные матема-

Синхронный генератор при частоте вращею1я, отличноii от

синхронной, можно приближенно рассматривать состоящим из двух машш1 - синхронной н асинхронной. Это лозБОJJяет рассматрнват-ь при анализе наложение ИJ1; синхронного и асинхрон нv rо мvмевтов

Урасненне вращающего момента турбины можно составить на основании стати ческих ха.рактернстнк Мт = 'Р (ro, µ), где µ - •е· лень открытия регулирующего кла11ана энергоносителя турбины.

Нелинейно спадающие характеристики Мт зависят от угловой ско­

рости турбины и степени открытия регулирующего клапана. При

 

 

медленных изменениях yrJювой скорости "11 открытия клапана при­ ближенно их предстамяют семей­

 

v

где критическое скольжение

Sкр = Sном (mmax + т;.., -1),

 

 

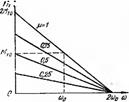
(12.14t

ством прямых(рис. 12. 1):

Мт = µ[M"-t],. (ro -ro0)), (12.7)

где Мт0, 000 - параметры, соответ­ ствующие ооминальному режиму; Чт - коэффнциеm саморегулиро­ вани<1 турбины.

Уравнение движения синхрон­

а mma.x. = Mm:u: /Мно." - кратность максимального момента.

В приближенных расчетах устойчивости электромагют1ые пе­

реходные процессы в асинхронном двигателе можно не учитывать,

/·

чго позволяет состаw1яющие e1u мощности описывать уравнениями"

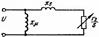
действительными для установившегося режима. Последние приме·

11итель110 к упрощенной схеме зимещення двигате.r1я (рис. 12.2, а}

имеют вид

 

Рис. 12.1. Идеализированные ха­

ного двигателя при Е' = const

Q = U r,si(r; +x;s); 1

(12.15i

2 2

Рактернстнки вращающего момента

Турбины

совпадает по составляющим с урав­

нением (11.4)

T,d2б/dt2 + М., = М, (12.8)

Q = Px,sir, + U2 (1 - а+ aU')lxµ.

v, z z l2

где Ммх - момент сопротивления рабочего механизма, и можеr нс­

пользооаться в расчетах кратковременных (до одного цикла кача­ 2

о

ний) переходных процессов. Допущение Е' = coпst приемлемо для

синхронных двигателей, которые электрически удалены от места а

возмущения, сохраняют устойчивость и слабо влпяют на режим других маши н. Расчетная э. д. с. Е' включена за переходным сопро­ тполением двигателя х и определяется выражением [271

Е' = Jf U• - 2U'Qx + (Р' +([') x '!U, (12.9)

где активная и реактивна< мощности двигателя ра эны:

Р = E'U sinб/x; Q = (U2 -E'U соsб)/х. (12.JO)

При расчете переходных нроцессов большой длительности сле­ дует иметь в виду, что переходные режимы генераторов характе­ ризуются ма11ыми скольжениями, тогда как скольжение синхронных двигателей может изменяться от ну.i1я до единицы. В этом случае нужно использовать уравне11ие движения сш1хронноrо двигателя

T,d2бidt2 + p,,dб/dt = М - М "" (12.11)

где p,jlб/dt - JJJt11еаризованный асинхронный момещ; Ра - коЭ<j,­

:рициент демпфирования, определяемый по линейной части асин­ хронной характеристнки синхронной машины как pd = dM!ds, а s = (ro0 - ro)/ro0 = dб/(ro.,dl) -скольжение двигателя.

Электромеханический переходный процесс дл я асинхронного