
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Совместно с численным решениемСодержание книги
Поиск на нашем сайте
EftD OL-L---'--'---- T,qn ft f2 Рис. 12.19. Характер из 1 1-1ения з. д. с. rенератора nри форси1ювке его возбуждения Аиалнз "устойч и системы с автоматическим регулятором пропорционалыюго типа показывает, чrо действие АРБ генератора позволяет расширить область статической устойчивости системы за предел б = rt/2, причем граница устойчивости находится в пре· целах, соответствующих s" =о и s =о. Q "• Оценка динамической устойчивости. Динамическую устойчи· вость простейшей электрической системы с автоматическим регу лятором пропорционального типа, в которой генератор работает на nmны неизменного напряжения, необходимо рассматривать с учетом нелинейности характеристик ее элементов. Смену режимов работы такой системы достаточно полно можно проанализировать на основе метода последовательных интервалов с линеари занией уравне11ий 11ереход11ых npouecco n 11а каждом ш1- rервале. Оценку устойчивости в этом случае выполняют по харак rеру изменения угла перемещения ротора ге11ератора во времени. Устройство форсировки возбуждения в самом простом варианте реализует закорачивание сопротивления в uепи ОВВ генератора nри снижении 11аnряже11ия на его зажимах J1IJ значения О,85Uг. t:Jpи Э'f()М ток в цепи ОВВ и nропорuиональноеему напряжение воз йуднтсля с учетом времени за11аздываиия t"0 01 срабатывания устройств АРВ (порядка О.05 с) возрастают до наиболЫ11его значе ния EtJt rns), оо экспоненциальному закону с постоя1111ой еремени возбудителя Т, (рис. 12.19). Так как э. д. с. в установившемся режиме генератора Е." уравнений его относmельноrо движения (12.106) в различных ре жимах. Приращение nродольной переходной з. д. с. за расчетный интервал времени определяется выражение м
где EtJt nрш1Иf\1ается средним за рассчитываемый п-й интервал времени. Определив приращение э. д. с. ЛЕ1n1, в п-м интервале можно nычислить полное значение продольной переходной э. д. с. в кон це рассчитываемого интервала
В момент возникновения аварийного L"ОСтояпия (КЗ) продоль ная переходная з. д. с. не изменяется, т. е. Е, = E;,OJ. Это ус ловие и является исходным при определении изменения по интер валам з. д. с. Е. В нормальном режиме Е = E.-I4 (x.-x). (12.138,а) где продо.льная сосrавляющая тока генератора вычис..1яется через внутреннюю реактивную Nощность генератора н значение син· хрооной э. д. с. Е.: 14 = Е,,у 11 cosa11 -Uy12 cos(б-a"). Пос. е подстановки н преобразовання (12.138,а) получим Е = Е.[1- (ха- х:)у" cosa"] + пропорциональн а, а в относительных едн1шuах равна иаnряжецню
+ Uy12 (xd -х:) cos (б- а 12). (12.138. б) Если емкостной проводимостью и активным сопротивлением элементов сети пренебречь, то с учетом тождеств х• - х == х. - - х и Ун== У12 <= их. выражение (12.138,б) приводится к упро- • щенному виду (12.111,б). Выражение (12.138,б) можоо использо·
Для каждого из последующих интервалов времени расчет по вторяют по последним пяти пунктам. Если при этом в n·м интервале времени угловая характеристика мощности генератора не меня ется, то приращение угла ному значе1шю переходной з. д. с. Е;: Е. = [E -Uy11 (X•-X)cos(б- по извест
А если меняется, то Лб<nJ = Лб,,,_ 11 +kЛР,,,_11,
Пор ок расчета динамической устойчивости простейшей злект· рическои системы с автоматическим регулятором пропорциональ ного типа с использованием зависимости 6 (/) следующий: 1. Составля1от хемы замещения сети для нормального, аварнй- 1юго и nослеаварииного режимов и определяют собственные, а так же взаимные проводимости и сопротиВJiеliия. 2. На основании расчета нормального режима устанавлив ают значения Р0, 60, Е.., Е.... 3. По заданныы характеристикам регулятора и возбудителя етроят кривую изменения э. д. с. Eqo (/) для установившегося режн>rа при форсировке возбуждения генератора. 4. Испо.оьзуя (12.139), вычисляют зиачеиие э. д. с. Е.м для первого момента после возникновения аварийного состояния (1<3). Расчетная формула при этом имеет вид E•tDJ = [Е... - Uy" (х. - х) cos (60 - -a12)]/[l -y11 (Xd-X)cos aн]. 5. Используя (12.136), находят приращение переходной э. д. с. в 1-ечеиие первого интервала времени: ЛЕ 111 = Лt (Е0,,.. - E«OJ)IT.0, где Е•® -среднее значение Е" за перБЫЙ интервал времени. 6. llo формуле (12.137) рассчитывают значение переходной э. д. с. в конце первого (начале второго) интервала времени: Е т = Е".о + ЛЕ щ- 7. Определяюг активную МощlЮСТь, отдаваемую генератором
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 (12.136)
(12.136) (12.137)
(12.137)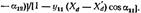 (12.139)
(12.139)


