
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графические способы описания систем: структурные схемы, графы, статические характеристики. Переход от одной формы к другой.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В теории управления широко применяется несколько графических способов описания системы управления: структурная схема, граф системы, статическая характеристика. Структурной схемой системы управления называют графическое представление ее математической модели в виде соединений звеньев с указанием входных и выходных сигналов. Основными элементами структурной схемы являются: звено, узел, сумматор и элемент сравнения.
Рисунок – Элементы структурных схем Графом называется совокупность множества V точек, называемых вершинами, и множества R простых (т.е. самонепересекающихся) кривых, называемых ребрами.
Рисунок – Граф системы управления
Статическая характеристика звена системы управления – зависимость выходного сигнала звена от входного сигнала в статическом режиме, представленная в графической форме. Режим работы САУ, в котором управляемая величина и все промежуточные величины не изменяются во времени, называется установившимся, или статическим режимом.
Рисунок – Виды статических характеристик звеньев
Переход от одной математической формы описания к другой Рассмотрим пример перехода от одной формы представления к другой. Дифференциальное уравнение объекта имеет вид:
Необходимо описать рассматриваемый объект с помощью известных форм. Запишем дифференциальное уравнение объекта в следующем виде:
Тогда, используя оператор дифференцирования
По формуле (1.7) передаточная функция в операторном виде для заданного объекта:
Заменив оператор дифференцирования
Задание №1.1 для объекта, заданного одной из форм описания линейной динамической системы, привести другие формы описания (за исключением формы пространства состояний).
В теории управления пространство состояний - один из основных методов описания поведения динамической системы.
Иногда возникает необходимость прямого и обратного перехода от записи системы в виде передаточной функции к форме описания с помощью пространства состояний. Прямой переход в такой задаче неоднозначен, т.е. существует бесконечное множество троек матриц, в то время как обратный переход однозначен. Существует три стандартных схемы перехода от передаточной функции к пространству состояний: последовательная схема, параллельная и нормальная.
Рассмотрим методику перехода по каждой схеме. Последовательная схема Задано дифференциальное уравнение, описывающее состояние системы:
Тогда передаточная функция для такой системы будет иметь вид:
Приведем передаточную функцию системы к виду последовательно соединенных звеньев первого порядка, т.е.
Структурная схема для такого вида передаточной функции имеет вид:
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:
Учитывая, что p – это оператор дифференцирования, т.е.
Тогда, принимая во внимание, что типовая форма записи метода пространства состояний имеет вид:
запишем матрицы A,B и C:
На основании полученных уравнений получим структурную схему для физической системы. Структурная схема физической системы это структурная схема специфической конфигурации, состоящая из интеграторов, коэффициентов усиления и сумматоров. Данная структурная схема представляет собой заготовку для исследования системы с использованием компьютера.
Параллельная схема Передаточная функция системы имеет вид:
Приведем передаточную функцию системы к виду параллельно соединенных звеньев первого порядка, т.е.:
Тогда запишем следующее:
Структурная схема для такого вида передаточной функции имеет вид:
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:
Учитывая, что p – это оператор дифференцирования, т.е.
Запишем матрицы A,B и C:
На основании полученных уравнений получим структурную схему для физической системы.
Нормальная схема Передаточная функция системы имеет вид:
Структурная схема для такого вида передаточной функции имеет вид:
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:
Учитывая, что p – это оператор дифференцирования, т.е.
Учитывая то, что при использовании метода пространства состояний матричная форма записи системы дифференциальных уравнений составляется относительно ДУ первого порядка, понизим уравнение второго порядка относительно сигнала
Запишем матрицы A,B и C:
На основании полученных уравнений получим структурную схему для физической системы.
Таким образом, используя три основных схемы перехода можно перейти от формы представления системы в виде передаточной функции к форме пространства состояний. Как уже было отмечено, существует и обратный путь перехода, т.е. от формы описания с помощью пространства состояния к операторной передаточной функции.
здесь Тогда относительно выходного сигнала можно записать:
а выражение для передаточной функции имеет вид:
здесь Таким образом, зная матрицы A, B и C, можно найти выражение для операторной передаточной функции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.96.41 (0.01 с.) |


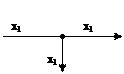



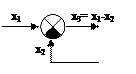



 .
. .
. , запишем уравнение объекта в операторном виде:
, запишем уравнение объекта в операторном виде: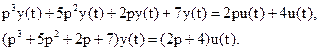 .
. .
. на оператор Лапласа
на оператор Лапласа  запишем передаточную функцию объекта в изображения Лапласа:
запишем передаточную функцию объекта в изображения Лапласа: .
.











 .
. .
. .
.

 , запишем
, запишем















 , введя промежуточный сигнал
, введя промежуточный сигнал  так, что
так, что
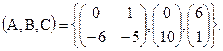


 - единичная матрица.
- единичная матрица. ,
, ,
, - обратная матрица для матрицы
- обратная матрица для матрицы  *.
*.


