
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые звенья и их характеристики: временные и частотныеСодержание книги
Поиск на нашем сайте
Для расчета и анализа система автоматического управления разбивается на динамические звенья. Динамическое звено – устройство любого физического вида и конструктивного оформления, описываемое дифференциальным уравнением. В соответствии с этим классификация звеньев производиться именно по виду дифференциальных уравнений.
Рисунок – Динамическое звено системы управления
В звеньях позиционного, статического типа входной и выходной сигналы в установившемся режиме связаны линейной зависимостью В звеньях интегрирующего типа линейной зависимостью В звеньях дифференцирующего типа линейной зависимостью В таблице 1 приведены передаточные функции основных типовых звеньев. Под типовым звеном понимается такое звено, которое описывается дифференциальным уравнением не выше второго порядка.
Таблица – Типовые звенья
Рассмотрим следующие типовые звенья: безынерционное (усилительное), апериодическое 1-го порядка, колебательное, консервативное, идеальное интегрирующее, идеальное дифференцирующее, форсирующее и звено с запаздыванием. Другие звенья подробно рассматривать не будем лишь потому, что все они получаются путем комбинации этих, элементарных звеньев.
5.1 Безынерционное (усилительное) звено Это звено мгновенно, без искажений воспроизводит входную величину на выходе. Примером может быть клапан с линеаризованной характеристикой в системах регулирования, различные усилители, рычажные передачи, редукторы и т.д. Уравнение движения усилительного звена имеет вид:
Передаточная функция такого звена тогда запишется как:
Подстановка
тогда выражения для ВЧХ и МЧХ будут записываться как:
тогда частотные характеристики АЧХ и ФЧХ:
Логарифмическая АЧХ звена в соответствии с выражениями:
Выражение для переходной функции и импульсной переходной функции звена:
Графики динамических характеристик приведены на рисунке.
Рисунок - Динамические характеристики безынерционного звена 5.2 Апериодическое звено 1-го порядка Апериодическое звено 1го порядка также называют инерционным. Примером таких звеньев может служить любая электрическая цепь, включающая сопротивление и емкость, различные тепловые объекты. Апериодическое звено первого порядка– это звено, выходной сигнал которого связан с входным сигналом следующим дифференциальным уравнением: где k, T – коэффициент усиления и постоянная времени звена соответственно. Тогда передаточная функция для данного звена будет иметь вид:
Подстановка
тогда выражения для ВЧХ и МЧХ можно найти как:
Выражения для АЧХ и ФЧХ рассматриваемого звена запишутся как:
График АФХ звена:
Логарифмическая амплитудно-частотная характеристика звена Построим асимптотическую характеристику L(ω) в низкочастотном диапазоне до частоты сопряжения На графике ЛАЧХ этому выражению соответствует прямая линия, параллельная оси частот. На частотах, много больших частоты сопряжения
Так как частота по оси абсцисс откладывается в логарифмическом масштабе, то этому выражению соответствует прямая линия с наклоном -20 дБ/дек. Переходная функция и функция веса звена имеют вид: h(t) =
5.3 Колебательное звено Колебательное звено - это звено, зависимость между выходным и входным сигналами которого описывается следующим дифференциальным уравнением где k, T – соответственно коэффициент усиления и постоянная времени звена; Передаточная функция звена:
Примерами реализации инерционного звена второго порядка являются RLC-контур, состоящий из катушки индуктивности, резистора и конденсатора, или физический маятник. Подстановка
Найдем выражения для ВЧХ и МЧХ:
Тогда выражения для АЧХ и ФЧХ могут быть получены как:
График АФХ приведен на рисунке:
В зависимости от значения коэффициента демпфирования Полюса передаточной функции колебательного звена – комплексно-сопряженные числа. Логарифмическая амплитудно-частотная характеристика звена примет вид:
Кусочно-асимптотическая ЛАЧХ звена состоит из двух участков. На низкочастотном участке до частоты сопряжения
а в диапазоне частот много больше частоты сопряжения уравнение высокочастотной асимптоты:
Последнее уравнение – это уравнение прямой с наклоном -40 дБ/дек. В окрестности частоты сопряжения график ЛАЧХ колебательного звена при Выражения переходной функции и функции веса колебательного звена:
Логарифмические характеристики для различных значений коэффициента
Временные характеристики для различных значений коэффициента
5.4 Идеальное интегрирующее звено Интегрирующее звено– это звено, выходной сигнал которого пропорционален интегралу по времени от входного сигнала: Передаточная функция звена:
Подстановка
Тогда выражения для АЧХ и ФЧХ могут быть записаны как:
Логарифмическая АЧХ звена с учетом (2.41) и (2.42) описывается выражением:
Графики логарифмической амплитудно- и фазочастотной характеристик приведены на рисунке:
Здесь же на рисунке приведены временные характеристики, выражения которых для интегрирующего звена имеют вид:
Примеры технической реализации интегрирующего звена: усилитель постоянного тока с большим коэффициентом усиления, в цепь обратной связи которого включен конденсатор. 5.5 Идеальное дифференцирующее звено Идеальное дифференцирующее звено – это звено, выходной сигнал которого пропорционален производной по времени от входного сигнала:
Передаточная функция звена:
Подстановка
Тогда выражения для АЧХ и ФЧХ могут быть записаны как:
Логарифмическая АЧХ звена описывается выражением:
Частотные характеристики звена приведены на рисунке:
Выражение для переходной характеристики звена:
Необходимо заметить, что в природе идеально дифференцирующего звена не существует.
5.6. Форсирующее звено Форсирующим звеном называется звено, описываемое уравнением:
Передаточная функция звена:
Подстановка
Тогда выражения для АЧХ и ФЧХ могут быть записаны как:
Частотные характеристики звена представлены на рисунке: (а) АЧХ, (б) ФЧХ, (в) АФХ
Временные характеристики звена получаются вида:
Графически изобразить можно только переходную характеристику:
5.7. Звено с запаздыванием Звено чистого запаздывания – это звено, выходной сигнал которого полностью совпадает по форме с входным сигналом, но отстает от него на время
На основании теоремы запаздывания* операторное дифференциальное уравнение имеет вид:
Следовательно, передаточная функция звена:
где Подстановка
Частотные характеристики звена представлены на рисунке: (а) АЧХ, (б) ФЧХ, (в) АФХ
Временные характеристики получаются по следующим уравнениям:
Графики временных характеристик представлены на том же рисунке, что и частотные, слева: сверху – входные сигналы, снизу – сигналы реакции.
5.8. Неминимально-фазовые звенья. Неминимально-фазовым называется звено, у которого хотя бы один нуль или полюс передаточной функции имеет положительную вещественную часть (является правым). Все рассмотренные ранее звенья относились к группе минимально-фазовых звеньев. Если же звено описывается типовым дифференциальным уравнением, но с отрицательным знаком перед одним из слагаемых, тогда мы можем говорить о неминимально-фазовых звеньях. Особенностью неминимально-фазовых звеньев в сравнении с минимально-фазовыми является то, что АЧХ этих звеньев совпадают, а отставание по фазе у неминимально-фазовых больше. Рассмотрим пример.
Подстановка
тогда выражения для ВЧХ и МЧХ можно найти как:
Выражения для АЧХ и ФЧХ рассматриваемого звена запишутся как:
Фазовая частотная характеристика при этом в общем виде записывается как:
здесь В нашем случае имеем один полюс, т.е. один положительный корень знаменателя передаточной функции, тогда ФЧХ:
Таким образом, для рассматриваемого звена фаза будет меняться от
Задание №5
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1720; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.27.41 (0.007 с.) |


 . Коэффициент пропорциональности
. Коэффициент пропорциональности  между входным и выходным сигналами представляет собой коэффициент передачи звена (в случае, если физическая природа сигналов различная, иначе – коэффициент усиления).
между входным и выходным сигналами представляет собой коэффициент передачи звена (в случае, если физическая природа сигналов различная, иначе – коэффициент усиления). связаны производная выходного сигнала и входной сигнал в установившемся режиме.
связаны производная выходного сигнала и входной сигнал в установившемся режиме. в установившемся режиме связаны выходной сигнал и производная входного.
в установившемся режиме связаны выходной сигнал и производная входного.












 .
. .
. дает выражение АФХ:
дает выражение АФХ: ,
,
 ,
, ,
, .
. .
.
 .
.
 ,
, .
. ,
,
 ,
, .
.
 .
. , пренебрегая в выражении для ЛАЧХ слагаемым, зависящим от частоты, так как оно много меньше единицы. В результате, получим:
, пренебрегая в выражении для ЛАЧХ слагаемым, зависящим от частоты, так как оно много меньше единицы. В результате, получим: .
. .
.
 w(t) =
w(t) =  .
.
 - коэффициент демпфирования.
- коэффициент демпфирования. .
. ,
,
 ,
, .
.
 ), колебательное (
), колебательное ( ) или апериодическое звено второго порядка (
) или апериодическое звено второго порядка ( ),.
),. .
.
 имеет амплитудный всплеск («горб»), величина которого тем больше, чем меньше коэффициент демпфирования
имеет амплитудный всплеск («горб»), величина которого тем больше, чем меньше коэффициент демпфирования  амплитудный всплеск вырождается в разрыв непрерывности.
амплитудный всплеск вырождается в разрыв непрерывности.
 ;
; =
=  ; где
; где  .
.
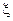 приведены на рисунке (а), на рисунке (б) представлены ЛЧХ для случая
приведены на рисунке (а), на рисунке (б) представлены ЛЧХ для случая 
 .
. .
. .
. ,
,  .
.
 .
.
 ,
,  .
. .
. .
. .
. ,
,  .
. .
.
 .
. .
. .
. .
. ,
,  .
.

 ,
,  .
.
 , т.е.
, т.е. .
.
 .
. ,
, .
.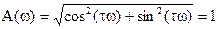 ,
, .
.

 ,
,  .
. - передаточная функция звена.
- передаточная функция звена. ,
,
 ,
, ,
, - количество корней с положительной вещественной частью, а знак зависит от того, корень числителя это или знаменателя.
- количество корней с положительной вещественной частью, а знак зависит от того, корень числителя это или знаменателя. .
. до
до  .
.


