
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Временные характеристики: способ получения, связь, показатели качества.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Говоря о математическом представлении системы помимо ранее рассмотренных способов используют также временные и частотные характеристики. Временная характеристика представляет собой функцию времени, описывающую выходной сигнал звена (или системы) при подаче на вход звена определенного тестирующего сигнала. Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе.
Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию на типовые входные воздействия, которые наиболее полно отражают особенности реальных возмущений. Во-первых, это позволяет сравнивать отдельные элементы между собой с точки зрения их динамических свойств. Во-вторых, зная реакцию системы на типовые воздействия, можно судить о том, как она будет вести себя при сложных изменениях входной величины.
Наиболее распространенными типовыми воздействиями являются: ступенчатое, импульсное и гармоническое воздействия. Указанные характеристики могут быть сняты экспериментально или построены по уравнению звена. К числу основных временных характеристик звена или системы относятся переходная функция и функция веса. Переходная функция звена представляет собой сигнал на выходе звена (реакцию звена), вызванный подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная ступенчатая функция, функция Хевисайда) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным. Единичное ступенчатое воздействие обозначается
Рисунок – Функция Хевисайда
Переходная функция обычно обозначается Наряду с переходной функцией при описании звеньев и систем применяется функция веса, общепринятое обозначение которой
Рисунок – Функция Дирака При этом согласно определению дельта-функции
Таким образом, Поскольку дельта-функция равна производной по времени от единичного ступенчатого воздействия, то и между переходной функцией, и функцией веса линейных звеньев существует аналогичная связь:
Временные характеристики могут быть выражены непосредственно через передаточную функцию звена с помощью преобразований Лапласа.
Рисунок– Динамическое звено системы управления Для звена, приведенного на рисунке, справедливо следующее соотношение:
Из определения переходной функции следует, что при подаче на вход звена сигнала
Таким образом, по заданной передаточной функции звена с помощью обратного преобразования Лапласа можно найти выражение для переходной функции:
Аналогичный вывод справедлив и для импульсной переходной функции с той лишь разницей, что
Приведем основные сведения о преобразовании Лапласа, которые будут использованы при рассмотрении систем, описываемых линейными дифференциальными уравнениями. Преобразованием Лапласа называют интегральное преобразование: определяющее соответствие между функцией а где Соотношение определяющее по известному изображению его оригинал (в точках непрерывности последнего), называют обратным преобразованием Лапласа. В нем интеграл берется вдоль прямой Re p = где Основные свойства (теоремы) преобразования Лапласа 1. Линейность преобразования. Для любых постоянных 2. Дифференцирование оригинала. Если производная где Если начальные условия нулевые, т.е.
В таблице приведены выражения изображения Лапласа для некоторых типовых сигналов. Изображения по Лапласу типовых сигналов
Прямые показатели качества
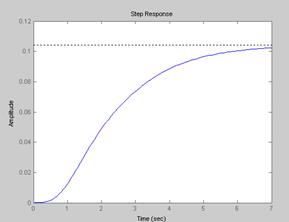
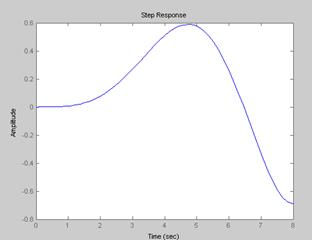
Если реакция системы на входное воздействие имеет установившийся характер (график сходящийся), то можно делать вывод о том, что система устойчива. Для оценки качества устойчивой системы полезно определить ряд показателей, которые кратко описывают некоторые характерные свойства динамики системы. Основные показатели качества системы: - hуст - установившееся значение – конечное значение переходной характеристики; - tн - время нарастания – время до момента, когда переходная характеристика впервые достигает значения hуст; - перерегулирование - - время регулирования tр – время, за которое переходный процесс заканчивается (с заданной точностью - число колебаний n – число колебаний переходной характеристики за время tр. Первый выброс не учитывается; - частота колебаний -
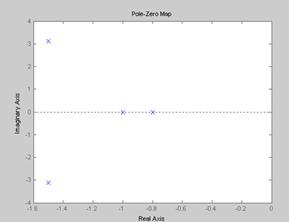
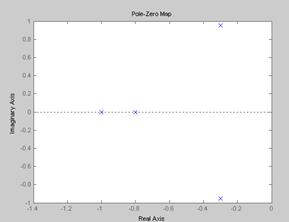
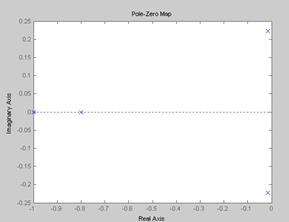
Связь расположения корней на комплексной плоскости и вида переходной характеристики.
По расположению корней характеристического уравнения системы на комплексной плоскости можно судить о виде переходной характеристики. Если все корни уравнения лежат слева от мнимой оси (а это свидетельствует об устойчивости системы), то переходная характеристика будет иметь установившийся характер, т.е. будет сходится к конечному значению; иначе переходная характеристики будет иметь расходящийся вид, амплитуда будет стремиться к бесконечности.
При этом на вид переходной характеристики влияет так же и вид корней: реальные или комплексные. Если среди корней характеристического уравнения будут комплексно сопряженная пара корней, то переходная характеристика будет иметь колебательный вид; если все корни будут вещественными, то переходная характеристика будет монотонной.
Задание №3*: Дано: дифференциальное уравнение системы
предполагается a 2 = 1, таблица с остальными коэффициентами дифференциального уравнения приведена ниже.
Требуется: 1) определить передаточную функцию W (s) системы; 2) найти переходную h (t) и импульсную переходную w (t) функции; 3) построить графики функций h (t) и w (t) на миллиметровке. Варианты задания
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.50.170 (0.007 с.) |

 и может быть описано следующим выражением:
и может быть описано следующим выражением:

 . Следовательно,
. Следовательно, 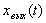 при
при  =
=  . Эта временная характеристика представляет собой реакцию звена на дельта-функцию (единичную импульсную функцию, иглу Дирака). Дельта-функция, которая обозначается
. Эта временная характеристика представляет собой реакцию звена на дельта-функцию (единичную импульсную функцию, иглу Дирака). Дельта-функция, которая обозначается  , – это математическая идеализация предельно короткого импульсного сигнала бесконечно большой амплитуды. Математически дельта-функцию можно описать следующим образом:
, – это математическая идеализация предельно короткого импульсного сигнала бесконечно большой амплитуды. Математически дельта-функцию можно описать следующим образом:

 .
. при
при 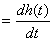 . И наоборот
. И наоборот .
.
 .
. , на выходе его будет сигнал
, на выходе его будет сигнал  . Так как при этом
. Так как при этом  и
и  , то из уравнения получим:
, то из уравнения получим: .
. .
. ,
, 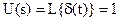 , тогда
, тогда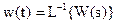 .
. , (2.6)
, (2.6) вещественного переменного и функцией
вещественного переменного и функцией 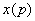 комплексного переменного
комплексного переменного 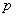 . При этом
. При этом  ,
, – оператор преобразования Лапласа.
– оператор преобразования Лапласа.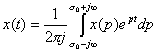 , (2.7)
, (2.7) . Символически обратное преобразование Лапласа можно записать так:
. Символически обратное преобразование Лапласа можно записать так: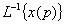 ,
, – символ обратного преобразования Лапласа.
– символ обратного преобразования Лапласа. и
и 
 . (2.8)
. (2.8) , где
, где  . И вообще, если n- я производная
. И вообще, если n- я производная  является функцией-оригиналом, то
является функцией-оригиналом, то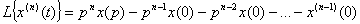 ,
, , k =0,1,… n -1.
, k =0,1,… n -1. , то последняя формула принимает вид:
, то последняя формула принимает вид: . (2.9)
. (2.9)


 )
) 

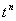





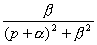

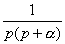



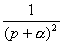


 ;
; ).
).  ;
; .
.













 ,
,


