
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы представления систем управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
План дополнительных занятий, I-ый семестр Курс – 20 часов, т.е. 8 занятий по 2 часа астрономических.
1 Способы представления систем управления. 1.1 Математические способы описания систем: дифференциальные уравнения, передаточные функции, пространство состояния. 1.2 Графические способы описания систем: структурные схемы, графы, статические характеристики. 1.3 Переход от одной математической формы описания к другой. 1.4 Переход от одной графической формы описания к другой. 2 Переход от одной формы описания системы к другой. 2.1 Правила эквивалентных преобразований структурных схем: последовательное, параллельное соединение и обратная связь. 2.2 Нахождение передаточной функции системы по структурной схеме для случая одноконтурных и многоконтурных систем, в том числе систем с перекрестными связями. 3 Временные характеристики: способ получения, связь, показатели качества. 4 Частотные характеристики: способ получения, связь, показатели качества. 5 Типовые звенья и их характеристики: временные и частотные. 5.1 Неустойчивые звенья. 6 Определение устойчивости системы. Теоремы Лапласа, критерии устойчивости. 6.1 Алгебраические критерии устойчивости. 6.2 Частотные критерии устойчивости. Определение устойчивости системы по ЛЧХ. 7 Построение областей устойчивости. D-разбиение. 8 MATLAB как средство анализа систем.
Теория автоматического управления (ТАУ) появилась во второй половине 19 века сначала как теория регулирования. Широкое применение паровых машин вызвало потребность в регуляторах, то есть в специальных устройствах, поддерживающих устойчивый режим работы паровой машины. Это дало начало научным исследованиям в области управления техническими объектами. Оказалось, что результаты и выводы данной теории могут быть применимы к управлению объектами различной природы с различными принципами действия. В настоящее время сфера ее влияния расширилась на анализ динамики таких систем, как экономические, социальные и т.п. Поэтому прежнее название “Теория автоматического регулирования” заменено на более широкое - “Теория автоматического управления”. Управление каким-либо объектом (объект управления будем обозначать ОУ) есть воздействие на него в целях достижения требуемых состояний или процессов. В качестве ОУ может служить самолет, станок, электродвигатель и т.п. Управление объектом с помощью технических средств без участия человека называется автоматическим управлением. Совокупность ОУ и средств автоматического управления называется системой автоматического управления (САУ).
Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин, характеризующих процессы, протекающие в ОУ, без непосредственного участия человека. Эти величины называются управляемыми величинами. Если в качестве ОУ рассматривается хлебопекарная печь, то управляемой величиной будет температура, которая должна изменяться по заданной программе в соответствии с требованиями технологического процесса.
Способы представления систем управления
Для исследования любой системы управления используется ее модель. Модель — это объект или явление, в достаточной степени повторяющие свойства моделируемого объекта или явления (прототипа), существенные для целей конкретного моделирования, и опускающие несущественные свойства, в которых они могут отличаться от прототипа. Виды моделей: 1 на естественном языке 2 на специальном языке 2.1 научные 2.1.1 математические формулы 2.1.2 алгоритмы 3 технические 3.1 техкарты 3.2 программы 4 Смешанные 4.1 таблицы 4.2 графы 4.2.1 деревья 4.2.2 сети 4.2.3 блок - схемы 4.3 схемы 4.4 карты 5 Наглядные (выраженные на языке представления) 5.1 рисунки 5.2 чертежи 5.3 графики 5.4 фотографии
В теории управления для исследования систем используются математические и смешанные (графические) способы описания систем.
Задание №1.1 для объекта, заданного одной из форм описания линейной динамической системы, привести другие формы описания (за исключением формы пространства состояний).
В теории управления пространство состояний - один из основных методов описания поведения динамической системы. Иногда возникает необходимость прямого и обратного перехода от записи системы в виде передаточной функции к форме описания с помощью пространства состояний. Прямой переход в такой задаче неоднозначен, т.е. существует бесконечное множество троек матриц, в то время как обратный переход однозначен. Существует три стандартных схемы перехода от передаточной функции к пространству состояний: последовательная схема, параллельная и нормальная.
Рассмотрим методику перехода по каждой схеме. Последовательная схема Задано дифференциальное уравнение, описывающее состояние системы:
Тогда передаточная функция для такой системы будет иметь вид:
Приведем передаточную функцию системы к виду последовательно соединенных звеньев первого порядка, т.е.
Структурная схема для такого вида передаточной функции имеет вид:
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:
Учитывая, что p – это оператор дифференцирования, т.е.
Тогда, принимая во внимание, что типовая форма записи метода пространства состояний имеет вид:
запишем матрицы A,B и C:
На основании полученных уравнений получим структурную схему для физической системы. Структурная схема физической системы это структурная схема специфической конфигурации, состоящая из интеграторов, коэффициентов усиления и сумматоров. Данная структурная схема представляет собой заготовку для исследования системы с использованием компьютера.
Параллельная схема Передаточная функция системы имеет вид:
Приведем передаточную функцию системы к виду параллельно соединенных звеньев первого порядка, т.е.:
Тогда запишем следующее:
Структурная схема для такого вида передаточной функции имеет вид:
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:
Учитывая, что p – это оператор дифференцирования, т.е.
Запишем матрицы A,B и C:
На основании полученных уравнений получим структурную схему для физической системы.
Нормальная схема Передаточная функция системы имеет вид:
Структурная схема для такого вида передаточной функции имеет вид:
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:
Учитывая, что p – это оператор дифференцирования, т.е.
Учитывая то, что при использовании метода пространства состояний матричная форма записи системы дифференциальных уравнений составляется относительно ДУ первого порядка, понизим уравнение второго порядка относительно сигнала
Запишем матрицы A,B и C:
На основании полученных уравнений получим структурную схему для физической системы.
Таким образом, используя три основных схемы перехода можно перейти от формы представления системы в виде передаточной функции к форме пространства состояний. Как уже было отмечено, существует и обратный путь перехода, т.е. от формы описания с помощью пространства состояния к операторной передаточной функции.
здесь Тогда относительно выходного сигнала можно записать:
а выражение для передаточной функции имеет вид:
здесь Таким образом, зная матрицы A, B и C, можно найти выражение для операторной передаточной функции.
Задание №4
Задание №5
Показатели качества системы
Для сравнительного анализа различных систем управления необходимо иметь некоторые числовые характеристики этих систем, позволяющие оценивать какая из них будет более эффективной. Эти числовые характеристики и называются критериями качества. Система управления характеризуется различными показателями, к которым в первую очередь можно отнести: точность, устойчивость, быстродействие надежность, стоимость, оптимальность и др. Учитывая большое разнообразие систем и объектов управления, в настоящее время разработано большое число различных критериев так или иначе включающих в себя вышеприведенные показатели. Между этими показателями (критериями качества) существует тесная взаимосвязь, поэтому стремление улучшить какой-либо показатель системы управления приводит к ухудшению другого. Так, например, стремление уменьшить ошибку регулирования приводит к уменьшению запаса устойчивости и быстродействия и наоборот, или повышение надежности системы неизбежно приводит к увеличению ее стоимости. Учитывая взаимосвязь между различными показателями систем управления задачу выбора или проектирования оптимальной системы можно рассматривать как задачу на условный экстремум. Найти экстремум (минимум и максимум) какого-либо показателя, например стоимости, при условии, что остальные показатели не превышают заранее заданной величины. Такой постановке отвечают интегральные критерии качества, представляющие собой определенные интегралы от некоторых функций переменных системы. Классификация показателей качества.
Наиболее полной характеристикой качества системы управления является ошибка e(t) =g(t)-y(t). Ошибка e(t), являясь функцией от времени, не очень удобна для оценки качества систем управления. Поэтому на практике при оценке качества чаще используют числовые показатели, которые прямо или косвенно характеризуют точность воспроизведения заданного движения. Ошибка e(t) зависит как от свойства системы управления (т. е. от уравнения), так и от внешнего воздействия. По этой причине показатели качества как характеристики свойства системы определяют при определенных внешних воздействиях, называемых типовыми. При оценке качества в переходном режиме в качестве типового воздействия используют ступенчатую функцию, а при оценке качества в установившемся режиме — полиномы времени t: At, At2,...
Прямыми показателями качества называются показатели, которые получаются непосредственно по переходной характеристике. Из прямых показателей качества наиболее часто используют время регулирования и перерегулирование.
Основные прямые показатели качества системы: - hуст - установившееся значение – конечное значение переходной характеристики; - tн - время нарастания – время до момента, когда переходная характеристика впервые достигает значения hуст; - перерегулирование - - время регулирования tр – время, за которое переходный процесс заканчивается (с заданной точностью - число колебаний n – число колебаний переходной характеристики за время tр. Первый выброс не учитывается; - частота колебаний -
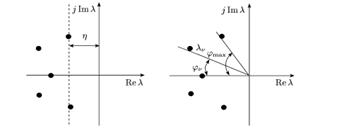
Корневые показатели качества. В качестве корневых показателей используют степень устойчивости и колебательность (степень колебательности). Степенью устойчивости системы управления (или характеристического полинома) называют расстояние от мнимой оси до ближайшего корня ее характеристического уравнения.
Степень колебательности, называемая также колебательностью, косвенно характеризует колебательность системы. Если степень колебательности равна нулю, то переходный процесс будет апериодическим. В общем случае можно ожидать, что при одинаковой степени устойчивости число колебаний за время регулирования будет больше у той системы, у которой больше степень колебательности.
По корневым показателям качества системы можно оценить значения основных прямых показателей качества:
Таким образом, степень устойчивости системы является косвенной мерой быстродействия системы. Степень колебательности, в свою очередь, является косвенной мерой устойчивости системы, причем чем величина степень колебательности меньше, тем больше запас устойчивости системы.
Частотные показатели качества. В качестве частотных показателей качества используют резонансный пик, полосу пропускания, запас устойчивости по фазе и запас устойчивости по амплитуде.
- M – частотный показатель колебательности, определяется по формуле:
- - - Показатель колебательности М характеризует запас устойчивости системы, чем выше показатель колебательности, тем меньше запас устойчивости. Допустимое значение М выбирается из условия М < 1,1-1,5. Величина частоты среза косвенной характеризует быстродействие системы:
при Помимо перечисленных частотных показателей качества, особое место занимают запасы устойчивости системы, которые определяются по АФХ разомкнутой системы или по ЛЧХ разомкнутой системы.
Запас устойчивости по амплитуде:
Запас устойчивости по фазе:
По логарифмическим характеристикам запас по фазе определяется по такому же соотношению, что и для определения запаса по АФХ, а для определения запаса по амплитуде используется следующая зависимость:
План дополнительных занятий, I-ый семестр Курс – 20 часов, т.е. 8 занятий по 2 часа астрономических.
1 Способы представления систем управления. 1.1 Математические способы описания систем: дифференциальные уравнения, передаточные функции, пространство состояния. 1.2 Графические способы описания систем: структурные схемы, графы, статические характеристики. 1.3 Переход от одной математической формы описания к другой. 1.4 Переход от одной графической формы описания к другой. 2 Переход от одной формы описания системы к другой. 2.1 Правила эквивалентных преобразований структурных схем: последовательное, параллельное соединение и обратная связь. 2.2 Нахождение передаточной функции системы по структурной схеме для случая одноконтурных и многоконтурных систем, в том числе систем с перекрестными связями. 3 Временные характеристики: способ получения, связь, показатели качества. 4 Частотные характеристики: способ получения, связь, показатели качества. 5 Типовые звенья и их характеристики: временные и частотные. 5.1 Неустойчивые звенья. 6 Определение устойчивости системы. Теоремы Лапласа, критерии устойчивости. 6.1 Алгебраические критерии устойчивости. 6.2 Частотные критерии устойчивости. Определение устойчивости системы по ЛЧХ. 7 Построение областей устойчивости. D-разбиение. 8 MATLAB как средство анализа систем.
Теория автоматического управления (ТАУ) появилась во второй половине 19 века сначала как теория регулирования. Широкое применение паровых машин вызвало потребность в регуляторах, то есть в специальных устройствах, поддерживающих устойчивый режим работы паровой машины. Это дало начало научным исследованиям в области управления техническими объектами. Оказалось, что результаты и выводы данной теории могут быть применимы к управлению объектами различной природы с различными принципами действия. В настоящее время сфера ее влияния расширилась на анализ динамики таких систем, как экономические, социальные и т.п. Поэтому прежнее название “Теория автоматического регулирования” заменено на более широкое - “Теория автоматического управления”. Управление каким-либо объектом (объект управления будем обозначать ОУ) есть воздействие на него в целях достижения требуемых состояний или процессов. В качестве ОУ может служить самолет, станок, электродвигатель и т.п. Управление объектом с помощью технических средств без участия человека называется автоматическим управлением. Совокупность ОУ и средств автоматического управления называется системой автоматического управления (САУ). Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин, характеризующих процессы, протекающие в ОУ, без непосредственного участия человека. Эти величины называются управляемыми величинами. Если в качестве ОУ рассматривается хлебопекарная печь, то управляемой величиной будет температура, которая должна изменяться по заданной программе в соответствии с требованиями технологического процесса.
Способы представления систем управления
Для исследования любой системы управления используется ее модель. Модель — это объект или явление, в достаточной степени повторяющие свойства моделируемого объекта или явления (прототипа), существенные для целей конкретного моделирования, и опускающие несущественные свойства, в которых они могут отличаться от прототипа. Виды моделей: 1 на естественном языке 2 на специальном языке 2.1 научные 2.1.1 математические формулы 2.1.2 алгоритмы 3 технические 3.1 техкарты 3.2 программы 4 Смешанные 4.1 таблицы 4.2 графы 4.2.1 деревья 4.2.2 сети 4.2.3 блок - схемы 4.3 схемы 4.4 карты 5 Наглядные (выраженные на языке представления) 5.1 рисунки 5.2 чертежи 5.3 графики 5.4 фотографии
В теории управления для исследования систем используются математические и смешанные (графические) способы описания систем.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.105.176 (0.016 с.) |













 .
. .
. .
.

 , запишем
, запишем















 , введя промежуточный сигнал
, введя промежуточный сигнал  так, что
так, что
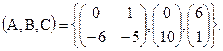


 - единичная матрица.
- единичная матрица. ,
, ,
, - обратная матрица для матрицы
- обратная матрица для матрицы  *.
*.

 ;
; ).
).  ;
; .
.
 .
. .
.



 ;
; - резонансная частота, частота, при которой АЧХ достигает максимальное значение;
- резонансная частота, частота, при которой АЧХ достигает максимальное значение; - граничная частота полосы пропускания системы;
- граничная частота полосы пропускания системы;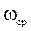 - частота среза, частота при которой
- частота среза, частота при которой  и затем АЧХ только убывает.
и затем АЧХ только убывает. ,
,


 , где а – расстояние от начала координат до точки пересечения АФХ отрицательной вещественной полуоси, т.е.
, где а – расстояние от начала координат до точки пересечения АФХ отрицательной вещественной полуоси, т.е.  .
. .
. .
.



