
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные критерии устойчивости: критерии Михайлова; следствие из критерия Михайлова.
Частотные критерии устойчивости: P=j a0(j Критерия Михайлова. Автоматическая система управления описываемая уравнением n-го порядка устойчива, если при изменение характеристический вектор повернется против часовой стрелки на угол Необращая при этом в 0. Следствие Михайлова: Автоматическая система устойчива, если действительные и мнимые части характеристической функции F(j P(
Вопрос14. Частотный критерий устойчивости Найквиста Этот критерий, разработанный в 1932 году американским ученым Г. Найквистом, дает правила, согласно которым по виду частотной характеристики разомкнутой цепи (Wгл(jw)) можно судить об устойчивости замкнутой системы. Рассмотрим структурную схему САУ в виде:
Рис. 4.14 Передаточная функция замкнутой САУ выражается через Передаточная функция замкнутой САУ выражается через W(s): Ф Пусть
Многочлен D(s) является характеристическим многочленом замкнутой системы, а Q(s) – характеристическим многочленом разомкнутой цепи этой системы. Степени этих многочленов равны. Частотный критерий Найквиста в этом случае формулируется следующим образом: Если разомкнутая цепь САУ неустойчива и ее характеристический многочлен Q(s) имеет m корней с положительной вещественной частью, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы АФЧХ разомкнутой системы W(jw) при изменении частоты w от 0 до ¥ охватывала точку (-1,j0) в положительном направлении m/2 раз. Например, если передаточная функция разомкнутой цепи имеет m=1 (один положительный полюс), то для устойчивости замкнутой системы АФЧХ разомкнутой цепи должна иметь вид, примерно как показано на рисунке 4.18,а, а в случае m=3 – как на рисунке 4.18,б. При этом начальная точка характеристики на оси абсцисс левее точки (-1,j0) считается как половина перехода.
Вопрос-15
Критерий Найквиста; логарифмический критерий Найквиста. Критерия Найквиста: Автоматическая система управления устойчива, если амплитудно фазное характеристика W(jω) разомкнутого контура не охватывает точку с координатой (-1; j0) Неустойчивая, если охватывает т. (-1; j0) Гранична, если проходит ч/з т. (1; j0) CАУ будет устойчива если при достижение фазы частотной характеристики 180 Данный критерий применяется при анализе устойчивости замкнутых систем, структурная схема которых показана на рисунке 12 Рисунок 12 Замкнутая САУ
Здесь W(p) – передаточная функция разомкнутой САУ. Предположим, что разомкнутая система устойчива. Тогда для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики W(jw) разомкнутой системы (указанная характеристика получается из W(p) заменой p=jw) не охватывал точку с координатами (-1, j0). Частота, на которой |W(jw)| = 1, называется частотой среза (wср). Для того, чтобы оценить, насколько далеко от границы устойчивости находится система, вводятся понятие запасов устойчивости. Запас устойчивости по амплитуде (модулю) указывает во сколько раз необходимо изменить длину радиуса-вектора годографа АФХ, чтобы, не меняя фазового сдвига, вывести систему на границу устойчивости. В свою очередь, запас устойчивости по фазе указывает, на сколько необходимо увеличить по абсолютной величине аргумент АФХ, чтобы, не меняя величину модуля, вывести систему на границу устойчивости. Для абсолютно устойчивых систем запас устойчивости по модулю DH вычисляется по формуле:
где частота w° определяется из соотношения arg W(jw°) = - 1800. Величина
Вопрос-16
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.135.186 (0.009 с.) |

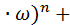 a1
a1 

 ,
, обращяется в 0 (ноль) по очереди т.е. корни уравнений P(
обращяется в 0 (ноль) по очереди т.е. корни уравнений P( 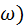 . jQ(
. jQ(  jQ(
jQ( 

 , где M(s) и Q(s) многочлены от S, причем степень многочлена M(s) - m меньше степени многочлена Q(s) - n. Тогда
, где M(s) и Q(s) многочлены от S, причем степень многочлена M(s) - m меньше степени многочлена Q(s) - n. Тогда

 а) Если в системе имеются местные обратные связи, то необходимо убедится в том, что по цепи местной обратной связи не нарушается устойчивость при разомкнутой главной обратной связи. Проверка устойчивости по цепи местной обратной связи может быть выполнена посредствам использования любых критериев устойчивости. Хотя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай надо избегать, стремясь использовать только устойчивыеместные обратные связи. В некоторых режимах работы при имеющихся в САУ нелинейностях в этом случае могут появиться автоколебания или произойдет потеряустойчивости
а) Если в системе имеются местные обратные связи, то необходимо убедится в том, что по цепи местной обратной связи не нарушается устойчивость при разомкнутой главной обратной связи. Проверка устойчивости по цепи местной обратной связи может быть выполнена посредствам использования любых критериев устойчивости. Хотя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай надо избегать, стремясь использовать только устойчивыеместные обратные связи. В некоторых режимах работы при имеющихся в САУ нелинейностях в этом случае могут появиться автоколебания или произойдет потеряустойчивости
 , амплитудная должна быть отрицательной.
, амплитудная должна быть отрицательной.

 = 180° + arg W(jwср) определяет запас устойчивости по фазе. Из критерия Найквиста следует, что устойчивая в разомкнутом состоянии система будет устойчивой и в замкнутом состоянии, если сдвиг по фазе на частоте среза не достигает – 1800. Выполнение этого условия можно проверить, построив логарифмические частотные характеристики разомкнутой САУ. При этом достаточно просто определяются также запасы устойчивости DН и
= 180° + arg W(jwср) определяет запас устойчивости по фазе. Из критерия Найквиста следует, что устойчивая в разомкнутом состоянии система будет устойчивой и в замкнутом состоянии, если сдвиг по фазе на частоте среза не достигает – 1800. Выполнение этого условия можно проверить, построив логарифмические частотные характеристики разомкнутой САУ. При этом достаточно просто определяются также запасы устойчивости DН и  , как показано на рисунке 13.
, как показано на рисунке 13.



