
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
J (w) - фазовая частотная характеристика (ФЧХ).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Графики частотных характеристик для любого типового звена можно определить расчетным путем через передаточную функцию звена W(p), заменяя комплексную переменную р на jw. Преобразованная функция называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой (АФЧХ): W(jw) = A(w) · ejj(w), где А(w) = | W(jw)|; j = arg W(jw). Для исследования частотных свойств используется нормированный входной синусоидальный сигнал, когда а = 1. В этом случае частотные характеристики выходного сигнала запишутся в следующем виде: W(jw) = k(w) · ejj(w); k(w) = | W(jw)|. В инженерных расчетах более удобно пользоваться частотными характеристиками, построенными в логарифмическом масштабе. При этом АЧХ, построенная в логарифмическом масштабе, будет называться логарифмической амплитудно-частотной характеристикой (ЛАЧХ) и запишется следующим образом L(w) = 20·lgA(w). В случае нормированного входного сигнала L(w) опишется выражением L(w) = 20 · lgk(w) [дБ]. За единицу измерения L(w) принят децибел (дБ). За единицу измерения частоты принимается декада, т.е. интервал частот, на котором частота изменяется в 10 раз: lgw [дек]. Билет-9 Логарифмические частотные характеристики.
Преобразованная функция называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой (АФЧХ): W(jw) = A(w) · ejj(w), где А(w) = | W(jw)|; j = arg W(jw). Для исследования частотных свойств используется нормированный входной синусоидальный сигнал, когда а = 1. В этом случае частотные характеристики выходного сигнала запишутся в следующем виде: W(jw) = k(w) · ejj(w); k(w) = | W(jw)|. В инженерных расчетах более удобно пользоваться частотными характеристиками, построенными в логарифмическом масштабе. При этом АЧХ, построенная в логарифмическом масштабе, будет называться логарифмической амплитудно-частотной характеристикой (ЛАЧХ) и запишется следующим образом L(w) = 20·lgA(w). В случае нормированного входного сигнала L(w) опишется выражением L(w) = 20 · lgk(w) [дБ]. Вопрос-10 Свойство объектов управления; математические модели простых объектов управления. Дифф. уравнение гидравлического объекта
Тепловой объект
Пневмадинамический объект.
Механический объект
Свойства; Самовыравнивание; Емкость; Запаздывание; Свойство объекта выведению из положения равновесия возвращяется к прежнему или переходит к новому равновесному состоянию без воздействия из вне называется самовыравниванием. Способность объекта накапливать энергию или вещества наз-ся аккумулирующей способностью, а величина характеризующая аккумулирующую способность объекта называется емкостью.Запаздывание проявляется в сдвиге по времени начало переходного процесса относительно входного воздействия. Вопрос- 11. Понятие устойчивости линейных непрерывных САУ Под устойчивость САУ понимается ее способность переходить из одного установившегося состояния (режима работы) в другое установившееся состояние под воздействием какого либовнешнего сигнала и оставаться в этом новом состоянии или возвращаться в исходное состояние при снятии этого воздействия.
Понятие «устойчивость» наглядно иллюстрируется на рис. (шар и опорная поверхность)На рис а,б шар находится в равновесии. При отклонении от этого положения в любую сторону в первом случае (а) шар не может вернуться в исходное положение (неустойчивое равновесие), во втором случае (б) – возвращается (устойчивое равновесие). Если опорная поверхность представляет собой горизонтальную плоскость, то шар движется по ней до тех пор, пока действует движущая сила Fд и после ее исчезновения останавливается в любой точке на плоскости. Такая система называется нейтральной (в). Систем устойчива в малом, если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом ее границы. Если границы устойчивости определены, т.е границы области начальных отклонений, при которых сис-ма возвращается в состояние равновесия,(г) и выяснено, что реальные начальные отклонения принадлежат этой области, то сист-ма устойчива в большом. Когда сис-ма возвращается в состояние равновесия при любых начальных отклонениях, ее называют устойчивой в целом, т.е и в малом и большом.Устойчивость САУ является необходимым условием ее работоспособности. Основоположником теории устойчивости является ученый математик А.М.Ляпунов, который в 1892 году опубликовал ряд теорем об устойчивости движения Устойчивость является одним из необходимых условий, обеспечивающих нормальное функционирование автоматических систем. Поэтому чрезвычайно важно выяснить те условия, которые обеспечивают принципиальную работоспособность системы, ее устойчивость. Признаком устойчивости САУ является существование установившегося состояния. Если отклонение выходной координаты от заданного значения (т. е. ошибка управления) не стремится к постоянной величине или к нулю, а возрастает или испытывает колебания, то САУ неустойчива. Причинами неустойчивости могут быть инерционность элементов и большой коэффициент передачи разомкнутой системы, так как многократно усиленное рассогласование, возвращающееся по цепи обратной связи на вход системы, не успевает из-за запаздывания в инерционных элементах отрабатываться.Не останавливаясь на теоремах, доказанных Ляпуновым, рассмотрим, как можно оценить устойчивость линейных систем, описываемых дифференциальным уравнением вида
Понятие устойчивости Устойчивость является одним из основных требований, предъявляемых к системам автоматического управления (САУ). Неустойчивые САУ неработоспособны, поэтому важно уметь определять и соответствующий выбор структуры и параметры системы, обеспечить её устойчивость. В системе управления требуется поддерживать некоторое заданное движение, которое называется невозмущенным движением.Вследствие различных возмущающих воздействий фактическое движение отличается от невозмущенного движения. В нормально функционирующей системе отклонение фактического движения от невозмущенного движения должно быть небольшим, а это возможно лишь в устойчивых системах. Устойчивость по входу Звено называется устойчивым по входу (осуществляющим устойчивое преобразование вход-выход), если при любом ограниченном входном воздействии x(t) и нулевых начальных условиях, выходная реакция y(t) является ограниченной при любом конечном и при и называется неустойчивым на входе в противном случае.Об устойчивости по входу можно судить по свойствам весовой функции Теорема 4.1 Для того, чтобы звено, описываемое операторным уравнением, было устойчиво по входу, необходимо и достаточно выполнение условия.Доказательство: известно, что вход и выход звена осуществляются по формуле.Пусть x(t) – произвольно правильная функция, т.е. такая, чтоГде С0 – некоторая константа. Тогда Характеристическое уравнение Устойчивость линейной системы зависит от её характеристического уравнения. Где дифференциальный параметр собственный P рассматривается, как переменная. Левая часть характеристического уравнения называется характеристическим полиномом.Характеристический полином системы совпадает с её собственным оператором или знаменателем передаточной функции. Необходимое и достаточное условие устойчивости Для того чтобы линейная непрерывная система была устойчива, необходимо и достаточно, чтобы все корни её характеристического уравнения Или другая формулировка.Для того чтобы линейная непрерывная система была устойчивой, необходимо и достаточно, чтобы все корни её характеристического уравнения были левыми, т.е. располагались в левой полуплоскости.
вопрос12. Критерий устойчивости Гурвица — один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицом. Наряду с критерием Рауса является представителем семейства алгебраических критериев устойчивости, в отличие от частотных критериев, таких, как критерий устойчивости Найквиста. Достоинством метода является принципиальная простота, недостатком - необходимость выполнения операции вычисления определителя, которая связана с определенными вычислительными тонкостями (например, для больших матриц может оказаться значительной вычислительная ошибка). Метод работает с коэффициентами характеристического уравнения системы. Пусть
Из коэффициентов характеристического уравнения строится определитель Гурвица 1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от 2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз; 3) на место коэффициентов с индексами меньше нуля или больше Тогда согласно критерию Гурвица: Для того, чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все Анализируя условие критерия Гурвица, можно заметить его избыточность. Число неравенств можно уменьшить в два раза, используя теорему Льенара-Шипара. Впрочем, в вычислительном отношении сложность критерия уменьшается не существенно, так как при вычислении минора высокого порядка чаще всего необходимо вычисление миноров низших порядков. Гурвица критерий, позволяющий узнать, когда все корни многочлена р (z) = a0zn + a1zn-1 +... + an-1z + an имеют отрицательные действительные части. Например, для многочленов с действительными коэффициентами a0 > 0, a 1,..., a nГ. к. гласит: чтобы все корни многочлена p (z) имели отрицательные действительные части, необходимо и достаточно, чтобы при всех k = 1, 2,..., n соблюдались неравенства:
Этот критерий был найден нем. математиком А. Гурвицем (A. Hurwitz) в 1895. Г. к. применяется главным образом для определения устойчивости решений системы линейных дифференциальных уравнений с постоянными коэффициентами (см. Устойчивость системы автоматического управления).
Вопрос-13
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.112 (0.013 с.) |








 Решение этого уравнения содержит две составляющие, одна из которых,
Решение этого уравнения содержит две составляющие, одна из которых,  (свободная или переходная составляющая), определяется решением однородного дифференциального уравнения:
(свободная или переходная составляющая), определяется решением однородного дифференциального уравнения:
 — передаточная функция системы, а
— передаточная функция системы, а  — характеристическое уравнение системы. Представим характеристический полином
— характеристическое уравнение системы. Представим характеристический полином  в виде
в виде
 по алгоритму:
по алгоритму: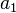 до
до  ;
; ставятся нули.
ставятся нули.



