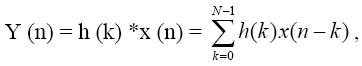Фильтры с конечной импульсной характеристикой (КИХ)

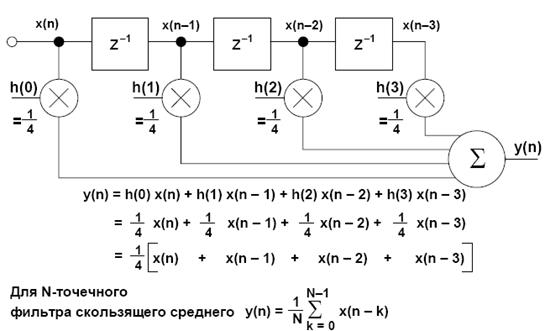
Существует два основных типа цифровых фильтров: фильтры с конечной импульсной характеристикой (КИХ) и фильтры с бесконечной импульсной характеристикой (БИХ). Как следует из терминологии, эта классификация относится к импульсным характеристикам фильтров. Изменяя веса коэффициентов и число звеньев КИХ фильтра, можно реализовать практически любую частотную характеристику. КИХ фильтры могут иметь такие свойства, которые невозможно достичь методами аналоговой фильтрации (в частности, совершенную линейную фазовую характеристику). Но высокоэффективные КИХ фильтры строятся с большим числом операций умножения с накоплением и поэтому требуют использования быстрых и эффективных процессоров DSP. С другой стороны, БИХ фильтры имеют тенденцию имитировать принцип действия традиционных аналоговых фильтров с обратной связь. Поэтому их импульсная характеристика имеет бесконечную длительность. Благодаря использованию обратной связи, БИХ фильтры могут быть реализованы с меньшим количеством коэффициентов, чем КИХ фильтры. Другим способом реализации КИХ или БИХ фильтрации являются решетчатые фильтры, которые часто используются в задачах обработки речи. Цифровые фильтры применяются в приложениях адаптивной фильтрации, благодаря своему быстродействию и простоте изменения характеристик воздействием на его коэффициенты.

Типы цифровых фильтров:

1) Фильтр скользящего среднего

2) Фильтр с конечной импульсной характеристикой (КИХ)

a) Линейная фаза

b) Легкость проектирования

c) Значительные вычислительные затраты

3) Фильтр с бесконечной импульсной характеристикой

a) Основаны на классических аналоговых фильтрах

b) Высокая вычислительная эффективность

4) Решетчатые фильтры (могут быть КИХ или БИХ)

5) Адаптивные фильтры

Элементарной формой КИХ фильтра является фильтр скользящего среднего (moving average), показанный на рисунке 1.3. Фильтры скользящего среднего популярны для сглаживания данных, например, для анализа стоимости акций и т.д. Входные отсчеты x(n) пропускаются через ряд регистров памяти (помеченных z^–1 в соответствии с представлением элемента задержки при z-преобразовании). В приведенном примере имеется четыре каскада, соответствующих 4-точечному фильтру скользящего среднего. Каждый отсчет умножается на 0,25, и результаты умножения суммируются для получения значения скользящего среднего, которое подается на выход y(n). На рисунке также представлено общее уравнение фильтра скользящего среднего на N точек. N относится к числу точек при вычислении фильтра, а не к разрешающей способности АЦП или ЦАП.

4-ТОЧЕЧНЫЙ ФИЛЬТР СКОЛЬЗЯЩЕГО СРЕДНЕГО

Рисунок 1.3 – 4-х точечный фильтр скользящего среднего.

 

С учетом равенства коэффициентов, наиболее простой путь исполнения фильтра скользящего среднего представлен на рисунке 1.4. Обратите внимание, что первым шагом является запоминание первых четырех отсчетов x(0), x(1), x(2), x(3) в регистрах. Эти величины суммируются и затем умножаются на 0,25 для получения первого выхода y(3). Обратите внимание, что начальные значения выходов y(0), y(1) и y(2) некорректны, потому что, пока отсчет x(3) не получен, не все регистры заполнены.

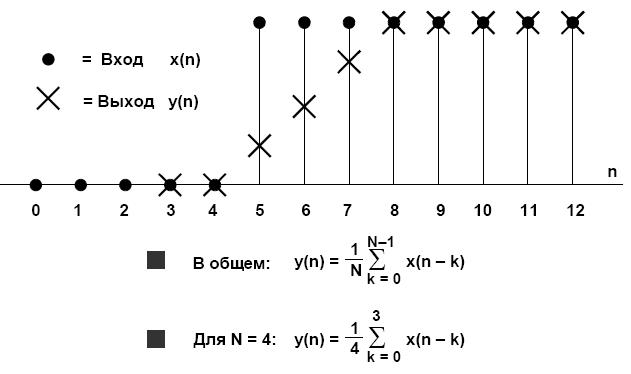
Рисунок 1.4 – Вычисление выходного сигнала фильтра скользящего среднего.

Когда получен отсчет x(4), он суммируется с результатом, а отсчет x(0) вычитается из результата. Затем новый результат должен быть умножен на 0,25. Поэтому вычисления, требуемые для получения нового значения на выходе, состоят из одного суммирования, одного вычитания и одного умножения, независимо от длины фильтра скользящего среднего.

Реакция 4-точечного фильтра скользящего среднего на ступенчатое воздействие представлена на рисунке 1.5. Скользящего среднего не имеет выброса по фронту входного сигнала. Это делает его полезным в приложениях обработки сигналов, где требуется фильтрация случайного белого шума при сохранении характера входного импульса. Из всех возможных линейных фильтров, фильтр скользящего среднего дает самый низкий уровень шума при заданной крутизне фронта импульса. Это показано на рисунке 1.6, где уровень шума понижается по мере увеличения числа точек. Существенно, что время реакции фильтра на ступенчатое воздействие от 0 % до 100 % равно произведению общего количества точек фильтра на период дискретизации.

Рисунок 1.5 – Реакция фильтра скользящего среднего на ступенчатое воздействие.

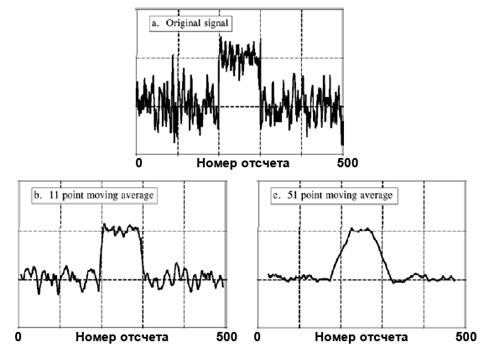
Рисунок 1.5 – Реакция фильтра скользящего среднего на воздействие в виде смеси шума и ступенчатого сигнала.

Частотная характеристика простого фильтра скользящего среднего выражается функцией sin(x)/x. Она представлена в линейном масштабе на рисунке 1.6. Увеличение числа точек при реализации фильтра сужает основной лепесток, но существенно не уменьшает амплитуду боковых лепестков частотной характеристики, которая равна приблизительно -14 дБ для фильтра с 11 и с 31 отводами (длиной буфера). Естественно, эти фильтры не подходят в том случае, где требуется большое ослабление в полосе задержания.

Рисунок 1.6 – АЧХ фильтра скользящего среднего.

Можно существенно улучшить эффективность простого КИХ фильтра скользящего среднего, выбирая разные веса или значения коэффициентов вместо равных значений. Крутизна спада может быть увеличена добавлением большего количества звеньев в фильтр, а характеристики полосы затухания улучшаются выбором надлежащих коэффициентов фильтра. Обратите внимание, что, в отличие от фильтра скользящего среднего, для реализации каждой ступени обобщенного КИХ фильтра требуется цикл умножения с накоплением. Сущность проектирования КИХ фильтра сводится к выбору соответствующих коэффициентов и необходимого числа звеньев при формировании желаемой частотной характеристики фильтра H(f). Для включения необходимой частотной характеристики H(f) в набор КИХ коэффициентов имеются различные алгоритмы и программные пакеты. Большинство этого программного обеспечения разработано для персональных компьютеров и доступно на рынке. Ключевой теоремой проектирования КИХ фильтра является утверждение, что коэффициенты h(n) КИХ фильтра являются просто квантованными значениями импульсной характеристики этого фильтра. Соответственно, импульсная характеристика является дискретным преобразованием Фурье от H(f).

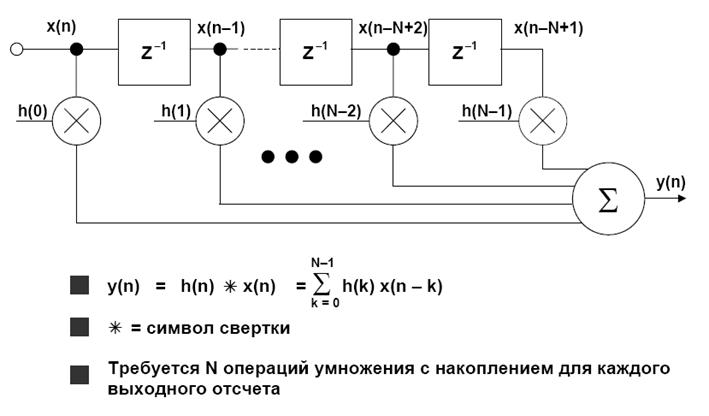
Рисунок 1.7 – Фильтр с конечной импульсной характеристикой порядка N.

 

Обобщенная форма КИХ фильтра с числом звеньев N представлена на рисунке 1.7. Как было сказано, КИХ фильтр должен работать в соответствии с уравнением, задающим свертку:

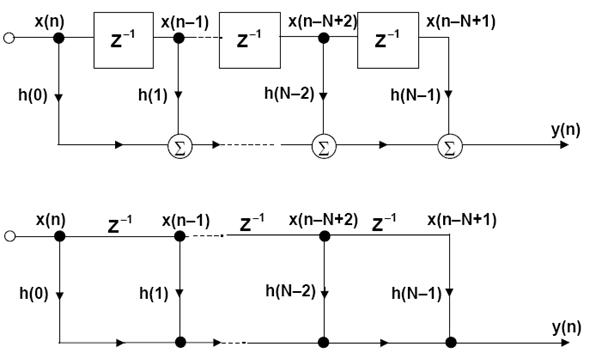
где h(k) – массив коэффициентов фильтра и x(n-k) – входной массив данных фильтра. Число N в уравнении представляет собой число звеньев и определяет эффективность фильтра, как было сказано выше. КИХ фильтр с числом звеньев N требует N циклов (операций) умножения с накоплением.

Согласно рисунке 1.8, диаграммы КИХ-фильтров часто изображаются в упрощенном виде. Операции суммирования представляются стрелками, указывающими в точки, а операции умножения обозначают, помещая коэффициенты h(k) рядом со стрелками на линиях. Элемент задержки z^-1 показывают, помещая его обозначение выше или рядом с соответствующей линией.

Рисунок 1.8 – Упрощенная схема фильтра.