
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статическая характеристика- это зависимость выходной переменной от входной в установившемся режиме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
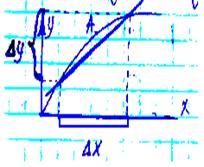
Методы линеаризации уравнений статики: 1 Метод малых отклонений. Основан на разложении аналитической функции у=f(х) в ряд Тейлора и отбрасывании малозначащих членов. Ду=/1(*о)+/1'( хо)Лхо +-А\х0)Ах2 +... 2) Метод касательной основан на замене участка кривой прямой линией, касательной к этой кривой в точке А (х0,у0), называемой рабочей точкой и находящегося в середине рабочего диапазона изменения ^х. y(x)=y(x0)+y’(x0)(x-x0) Δy=k Δx y-y0=y’(x0)(x-x0) k-передаточный коэффициент k=y’(x0) Δy=y’(x) Δx Метод по секущей основан на замене уравнения урав нелинейной характеристики урав секущей, параметры которого определяют методом наименьших квадратов.
модели динамики. Они имеют вид уравнений, описывающих изменение во времени выходных величин систем (элементов) в зависимости от изменения входных. Такой режим (процесс) функционирования системы называют переходным и описывают дифференциальными уравнениями. Частный случай переходного режима — установившийся, характеризуемый независимостью входных и выходных координат от времени. Этот режим описывается дифференциальными уравнениями нулевого порядка, т. е. алгебраическими уравнениями, получаемыми из уравнений динамики приравниванием к нулю всех производных по времени. Вопрос 5 Понятие о передаточной функции
Передаточная функция – это отношение лапласового изображения выходной величины к лапласовому изображеню входной величины при нулевых начальных условиях.
Корни характеристического уравнения называется полюсами. Вопрос-6 Временные характеристики САУ: переходная и импульсная функции. Временные характеристики определяют вид изменения выходного сигнала при подаче на вход звена типового управляющего воздействия. Это позволяет сравнивать свойства звеньев в динамических режимах работы. Временные свойства звена определяются, его переходной и импульсной переходной характеристиками. Переходная функция h(t)- это изменение выходной величины y(t) во времени возникающее после подачи на вход в единичного ступенчатого воздействия при нулевых начальных условиях.
Импульсная функция – это реакция элемента на импульсное воздействие,которое описывается дельта-функцией Дирака
Вопрос 7 Типовые динамические звенья САУ: классификация, передаточные функции. Типовыми динамическими звеньями называются звенья, описываемые дифференциальными уравнениями не выше второго порядка. Для моделирования структурных схем систем автоматического управления (САУ) используются три группы типовых звеньев:1. позиционные;2.интегрирующие; Дифференцирующие. Позиционные звенья описываются линейными дифференциальными уравнениями не выше второго порядка. Основное свойство устойчивых позиционных звеньев: при постоянном входном сигнале входная величина с течением времени стремится к постоянному значению. Интегрирующие звенья. В этих звеньях выходная величина X в установившемся режиме пропорциональна интегралу по времени от входной величины U. Дифференцирующие звенья. В этих звеньях выходная величина X в установившемся режиме пропорциональна производной по времени от входной величины U. 1)Позиционные: Безинерционное (пропорциональное) W(p) = k, где k = k*1(t) Апериодическое 1-го порядка Апериодическое 2-го порядка Колебательное Консервативное Интегрирующие Идеальное интегрирующее W(p)= Интегрирующее с запаздыванием (инерционные) Дифференцирующее Идеальное дифференцирующее W(p)=kp Дифференцирующее с запаздыванием (инерционные) W(p)= Вопрос-8 Если на вход любого динамического звена подать синусоидальные колебания y = a·sin w1t с амплитудой а и частотой w, то на выходе звена установятся "вынужденные" синусоидальные колебания x = A·sin(w1 + j) с амплитудой A = k × a, частотой w1 сдвинутые по фазе на угол j. Коэффициент усиления звена k = А/а. При изменении частоты w коэффициент усиления звена и сдвиг фазы будут изменяться. Эти зависимости представляются в виде частотных характеристик:
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 637; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


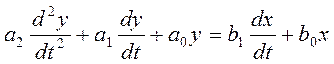 неоднородное дифференциальное уравнение 2 порядка
неоднородное дифференциальное уравнение 2 порядка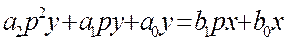 уравнение системы в оперативной форме
уравнение системы в оперативной форме 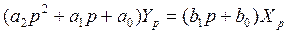 оперативная форма
оперативная форма - изображения
- изображения 



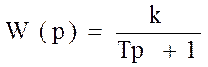
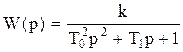 или
или 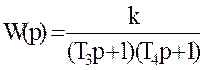
 где
где 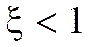
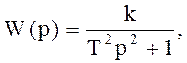
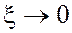

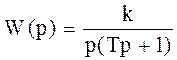
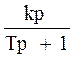
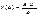 k (w) - амплитудная частотная характеристика (АЧХ);
k (w) - амплитудная частотная характеристика (АЧХ);


