Теорема об изменении кинетической энергии системы.

Опр. Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости: [Дж = Н*м]

Опр. Кинетической энергией системы называют сумму кинетических энергий всех точек системы

Теорема(1). Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему: .

Теорема(2). Изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек системы при том же перемещении системы: .

Теорема(3). Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке: .

Теорема Кенига. Кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы при ее движении относительно центра масс:

При плоско-параллельном движении тела кинетическая энергия состоит из суммы двух слагаемых: кинетическая энергия в поступательном движении вместе с центром масс и кинетическая энергия тела при вращении вокруг центра масс.

1. Кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для одной точки, у которой масса равна массе этого тела.

, - скорость любой точки твердого тела

2. Кинетическая энергия твердого тела при вращательном движении вокруг неподвижной оси равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.

, - угловая скорость вращения твердого тела.

3. Кинетическая энергия твердого тела при плоском движении складывается из кинетической энергии тела вместе с центром масс и кинетической энергии тела от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.

, - скорость центра масс твердого тела, - угловая скорость вращения твердого тела.

Вычисление работы сил

Опр. Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.

, где j - угол между и .

Полная работа силы вычисляется через интеграл или

Работа силы в некоторых случаях

1. Сила постоянна по величине. Точка или тело движется прямолинейно: ,

2. Работа силы тяжести: ,

3. Работа силы при вращательном движении тела вокруг неподвижной оси: , .

Если М=const, то , где j - угол поворота.

4. Работа силы упругости пружины.

Если x₀ = 0, то , l - удлинение пружины.

Единицей измерения работы в СИ является – 1 Н·м = 1 Дж

Опр. Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы: [Дж/с = Вт]

Мощность равна скалярному произведению силы на скорость:

В технике за единицу силы принимается 1 л.с. = 736 Вт = 75 кг·м²/с³.

Принцип Даламбера для материальной точки

Уравнение движения материальной точки относительно инерциальной системы отсчета под действием приложенных активных сил и сил реакции связей имеет вид: , где - равнодействующая активных сил, - равнодействующая сил реакции связей.

Силой инерции материальной точки называют произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е. .

Принцип Даламбера. При движении материальной точки активные силы и силы реакции связей вместе с силой инерции точки образуют равновесную систему сил:

Принцип Даламбера называют еще методом кинетостатики. Задачи динамики с помощью этого метода сводятся к задачам статики.

Аналитическая механика. Основные понятия.

Связи - ограничения, накладываемые на координаты и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах. (Конструктивно связи могут быть реализованы с помощью шарниров, стержней, нитей, поверхностей и т.д.)

Аналитически связи выражаются уравнениями или неравенствами:

, , где - число точек системы, - количество связей.

Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции связи или реакцией связи.

Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу.

Силы, не являющиеся реакциями связи (например, сила тяжести), называются активными силами.

Активные силы не зависят (модуль и направление) непосредственно от других действующих на тело сил. Сила реакции связи отличается от действующих на тело активных сил тем, что её численная величина всегда зависит от этих сил и неизвестна заранее. Если нет никаких активных сил, то реакции связей равны нулю.

Опр. Голономная система — механическая система, все механические связи которой можно свести к геометрическим (то есть, к голономным). Такие связи сводятся к ограничениям только на положения тел системы. Связи, не сводящиеся к геометрическим, называются неголономными.

Опр. Возможные перемещения системы – любая совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент всеми наложенными на систему связями.

При стационарных связях действительное перемещение совпадает с одним из возможных.

Число степеней свободы

Рассмотрим систему из N материальных точек, на которую наложено l голономных связей , ; .

Здесь - число независимых координат (обобщенных координат), которые полностью определяют положение системы в любой момент времени. Это и есть число степеней свободы.

Принцип возможных перемещений (определение равновесия системы)

Для равновесия механической системы, подчиненной идеальным, стационарным и неосвобождающим связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, приложенных к точкам системы, была равна нулю на любом возможном перемещении системы, если скорости точек системы в рассматриваемый момент времени равны нулю, т. е. , k – точки приложения сил и их возможные перемещения, - это любое возможное перемещение.

Общее уравнение динамики (принцип Даламбера-Лагранжа)

Теорема. Сумма элементарных работ всех активных и сил инерции равна нулю на любом возможном перемещении системы. или .

Замечание: Вычисление работ сил инерции:

1. Поступательное движение:

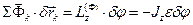2. Вращение вокруг неподвижной оси твердого тела: (здесь направлено по ε).

3. При плоском движении: , здесь - главный момент сил инерции относительно оси z проходит через центр масс, - вариация перемещения центра масс.