
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Т. М. 9. Сложное движение точки. Абсолютная скорость и абсолютное ускорение точки в сложном движении.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В ряде случаев движение точки можно рассматривать по отношению к двум системам отсчета, из которых одну можно считать условно неподвижной. Например, движение человека по движущейся лодке по отношению к берегу является сложным, состоящим из движения относительно лодки (подвижная система отсчета) и движение вместе с лодкой по отношению к берегу (неподвижная система отсчета). Движение точки относительно неподвижной системы отсчета называется абсолютным движением. Движение точки относительно подвижной системы отсчета называется относительным. Движение точки вместе с подвижной системой отсчета относительно неподвижной системы отсчета является для точки переносным. При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей. Если переносным движением является вращательное движение, переносной скоростью
Численное значение скорости Модуль абсолютной скорости определяется по правилу параллелограмма
Абсолютное ускорение точки равно геометрической сумме трех ускорений: - относительного - переносного - ускорения Кориолиса
Т.М. 10. Ускорение Кориолиса. Его модуль и направление.
Относительное и переносное ускорение определяется из закона соответствующего движения. Ускорение Кориолиса вычисляется по формуле Ускорение Кориолиса равно нулю, если а) б) векторы Чтобы определить направление векторы ускорения Кориолиса по правилу Жуковского необходимо: 1) перенести в точку М вектор угловой скорости переносного вращательного движения; 2) спроецировать вектор относительной скорости 3) повернуть проекцию
Если переносное движение поступательное, то
При решении задач на сложное движение точки рекомендуется придерживаться следующего порядка: 1. выяснить, какое движение точки является абсолютным, какое относительным и какое переносным. 2. используя закон относительного движения, определить положение точки в заданный момент времени. 3. вычислить относительную и переносную скорость точки, показать векторы переносной и относительной скорости. Вычислить абсолютную скорость точки по правилу параллелограмма или по проекциям на координатные оси. 4. вычислить составляющие относительного и переносного ускорений и показать на схеме их векторы. 5. в случае переносного вращательного движения определить модуль и направление ускорения Кориолиса. 6. вычислить модуль абсолютного ускорения точки по проекциям на координатные оси.
Т.М. 11. 4 закона динамики. Первый закон динамики (закон инерции): Материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока действие каких-либо сил не выведет ее из этого состояния. Равномерное и прямолинейное движение точки называют движением инерции. Покой является частным случаем движения по инерции, когда скорость точки равна нулю. Всякая материальная точка обладает инертностью, т.е. стремиться сохранить состояние покоя или равномерного прямолинейного движения. Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной, а движение, наблюдаемое по отношению к этой системе, называется абсолютным. Любая система отсчета, совершающая относительно инерциальной системы поступательное прямолинейное и равномерное движение, будет также инерциальной системой.
Второй закон (основной закон динамики): Ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и совпадает с силой по направлению: Из основного закона динамики следует, что при силе Третий закон (закон действия и противодействия): Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены вдоль одной прямой в противоположны е стороны. Силы, именуемые действием и противодействием, приложены к разным телам и поэтому уравновешенной системы сил не образуют. Четвертый закон динамики (закон зависимости действия сил): При одновременном действия нескольких сил ускорение материальной точки равно геометрической сумме ускорений, которые имела бы точка при действии каждой силы в отдельности:
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.103.119 (0.011 с.) |

 , где
, где 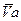 - абсолютная скорость точки в движении относительно неподвижной системы отсчета;
- абсолютная скорость точки в движении относительно неподвижной системы отсчета;  - относительная скорость точки, скорость движения относительно подвижной системы отсчета;
- относительная скорость точки, скорость движения относительно подвижной системы отсчета;  - переносная скорость точки, скорость той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
- переносная скорость точки, скорость той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
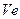 зависит от угловой скорости вращающегося тела и расстояния
зависит от угловой скорости вращающегося тела и расстояния 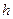 точки оси вращения. Расстояние
точки оси вращения. Расстояние 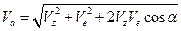 . Если векторы
. Если векторы  лежат в одной плоскости, то модуль абсолютной скорости удобно определить по проекциям на координатные оси
лежат в одной плоскости, то модуль абсолютной скорости удобно определить по проекциям на координатные оси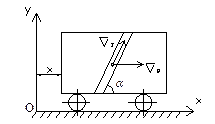
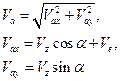
 , характеризующего изменение относительной скорости точки в относительном движении;
, характеризующего изменение относительной скорости точки в относительном движении;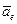 , характеризующего изменение переносной скорости точки в переносном движении;
, характеризующего изменение переносной скорости точки в переносном движении;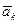 , характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении
, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении  .
.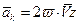 , где
, где 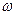 - угловая скорость переносного вращательного движения. Модуль ускорения Кориолиса зависит от угла между векторами
- угловая скорость переносного вращательного движения. Модуль ускорения Кориолиса зависит от угла между векторами 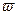 и
и 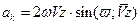 .
. , т.е. переносное движение не является вращательным;
, т.е. переносное движение не является вращательным; .
. на 900 в сторону вращения.
на 900 в сторону вращения.
 , поэтому абсолютное ускорение будет равно геометрической сумме относительного и переносного ускорений.
, поэтому абсолютное ускорение будет равно геометрической сумме относительного и переносного ускорений.

 .
. ускорение
ускорение 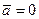 . Масса точки характеризует степень сопротивляемости точки изменению ее скорости, т.е. является мерой инертности материальной точки.
. Масса точки характеризует степень сопротивляемости точки изменению ее скорости, т.е. является мерой инертности материальной точки. .
.


