
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угловая скорость при вращении тела вокруг неподвижной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.
Рассмотрим бесконечно малый промежуток времени Δt → 0, за который твердое тело совершает поворот на бесконечно малый угол Δα вокруг мгновенной оси Ω (рисунок 3.2).
Рис. 3.2
Предел, к которому стремится отношение Δα / Δt, называется угловой скоростью твердого тела в рассматриваемый момент времени
Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки. Угловое ускорение при вращении тела Угловым ускорением называют степень изменения угловой скорости.
За вектор углового ускорения ε при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости ω в данный момент как по числовой величине, так и по направлению. Такой характеристикой является производная по времени от вектора угловой скорости ω. Таким образом, угловое ускорение определяется так:
Рис. 3.3
В общем случае угловое ускорение не направлено по мгновенной оси, а, как производная по времени от вектора ω, параллельно касательной к годографу этого вектора. Условимся угловое ускорение ε изображать в любой точке прямой, параллельной этой касательной годографа угловой скорости u, но проходящей через неподвижную точку тела (рисунок 3.3). Прямая, по которой направлен вектор углового ускорения, называется осью углового ускорения и обозначается E.
Кинематика твердого тела В кинематике твердого тела определяются: закон движения и кинематические характеристики тела, а также кинематические характеристики точек тела.
В данном методическом пособии рассмотрены следующие виды движения твердого тела: - поступательное; - вращательное; - плоскопараллельное. Поступательное движение Поступательное движение – это движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе.
На рисунках 2.1,а и 2.1,б приведены примеры поступательного движения: движение прямоугольника в плоскости чертежа, движение каждой кабины колеса обозрения.
а б Рисунок 2.1
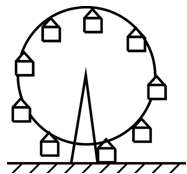
Рисунок 2.2 Исходя из определения поступательного движения, движение твердого тела может быть задано в векторном виде формулой (рисунок 2.2): rM=rA ⊕ AM.
В этой формуле AM - вектор постоянный по величине и направлению, поэтому производная от него равна нулю. Для скорости и ускорения произвольной точки M получим:
То есть скорости и ускорения точек твердого тела при поступательном движении равны и одинаково направлены, а траектории при наложении совпадают.
Для определения кинематических характеристик точек тела достаточно знать закон движения одной из них.
Движение твердого тела, при котором две его точки О и О ' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО ' называют осью вращения.
Рис. 2.12 Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение d r.
Угловой скоростью называется вектор
Если ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси. Пусть v – линейная скорость точки М. За промежуток времени dt точка М проходит путь dr = vdt. В то же время dr = Rd φ (dφ - центральный угол). Тогда, можно получить связь линейной скорости и угловой:
В векторной форме Наряду с угловой скоростью вращения используют понятия периода и частоты вращения.
Введем вектор углового ускорения
Вектор
Рис. 2.13 Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:
Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота), направлены вдоль оси вращения. равномерное вращение ε = 0; ω = const; φ = φ0 ± ω t, равнопеременное вращение
Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11).
При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M1M2) совершают одинаковые движения.
Рисунок 2.11
Рисунок 2.12
Отрезок M1M2 движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.
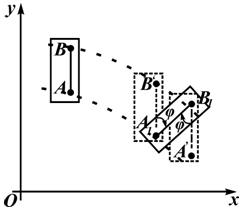
На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A с последующим поворотом на угол φ вокруг точки A1. Это же перемещение можно выполнить иначе.
Например, перемещая пластинку поступательно с траекторией точки B, с последующим поворотом вокруг B1 на угол φ. Траектории точек A и B различны, а угол поворота в обоих случаях одинаков.
Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде: xA=xA(t), yA=yA(t), φ=φ(t). Точка A в этом случае называется полюсом. Если принять за полюс точку B, то получим уравнения: x B=xB(t), yB=yB(t), φ=φ(t)
За полюс выбирается точка, закон движения которой известен.
ИНЕРЦИАЛЬНАЯ система ОТСЧЕТА - система отсчета, в которой справедлив закон инерции: материальная точка, на которую не действуют никакие силы, находится в состоянии покоя или равномерного прямолинейного движения. Любая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета. Все инерциальные системы отсчета равноправны, т. е. во всех таких системах законы физики одинаковы. Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v0.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система K будет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x',y',z' системы K' так что оси x и x' совпадали, а оси y и y', z и z', были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x',y',z' той же точки в системе K'. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x'+v0, кроме того, очевидно, что y=y', z=z'. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t'. Получим совокупность четырёх уравнений: x=x'+v0t;y=y';z=z';t=t', названных преобразованиями Галилея Инвариантами преобразования Галилея являются длина тел и промежуток времени между событиями. Именно поэтому понятия длины и промежутка времени играют такую большую роль в классической физике. [ 4 ] Дифференциал dr являетсяинвариантом преобразований Лоренца, т.е. интервалом времени, не зависящим от ситуации - подвижной или неподвижной является исходная система отсчета. Ньютона о существовании некоего универсального, абсолютного времени. [ 13 ] скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно движущейся системы и скорости самой движущейся системы относительно неподвижной
В классической механике справедлив механический принцип относительности: законы динамики одинаковы во всех инерциальных системах отсчета. Рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), условно будем считать неподвижной, и систему К' (с координатами x', y', z'), движущуюся относительно К равномерно и прямолинейно со скоростью υ0 (υ0=const)
Координата точки А по отношению к системе К: х = х' + 00', за промежуток времени t от начала отсчета будет:
Уравнения (3.19) носят название преобразования координат и времени Галилея. Отсчет времени начат с момента, когда начало координат обеих систем совпадают. Продифференцировав по времени t, получим выражение правила сложения скоростей в классической механике: υ=υ'+υ0 (3.20) Ускорения в обеих системах отсчета одинаковы, а это означает, что поведение тел в обеих системах одинаково: a=a' (3.21), т.е. из соотношения (3.21) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными по отношению к преобразованиям Галилея. Механический принцип относительности можно сформулировать еще следующим образом: никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.
11. Закон ньютона Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета. 12.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1061; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |


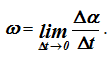











 , ни вторая производная
, ни вторая производная  не могут служить характеристикой движения всего твердого тела.
не могут служить характеристикой движения всего твердого тела.  , проведенный из точки 0 ' в точку М, повернется на угол d φ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться).
, проведенный из точки 0 ' в точку М, повернется на угол d φ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться). 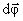 – вектор элементарного поворота тела, численно равный d φ и направленный вдоль оси вращения ОО ' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора
– вектор элементарного поворота тела, численно равный d φ и направленный вдоль оси вращения ОО ' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора 
 , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении
, численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении  .
.
 .
.
 .
.  ортогонален к векторам
ортогонален к векторам  .
. ,
,  ,
,  .
. для характеристики неравномерного вращения тела:
для характеристики неравномерного вращения тела: .
.
 направлен в ту же сторону, что и
направлен в ту же сторону, что и  , а
, а  направлен в противоположную сторону при замедленном вращении
направлен в противоположную сторону при замедленном вращении 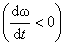 (рис. 2.13).
(рис. 2.13).


 .
.


 (3.19)
(3.19)


