
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика твердого тела. Углы Эйлера, угловая скорость.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Координаты любой точки твердого тела можно задать как относительно неподвижной системы координат с помощью радиуса-вектора Дифференцируя равенство (6.1) по времени, получим следующее выражение для скорости некоторой точки твердого тела: Здесь
Угловая скоростъ твердого тела не зависит от положения подвижиого начала координа. Перенесем начало подвижной системы координат из точки о в точку о ' вдоль вектора
Здесь
где векторы
Тензор инерции Запишем момент импульса
Здесь Будем рассматривать только момент импульса и кинетическую энергию, обусловленные вращением тела, и отбросим индекс «вращ». Раскрывая в формуле (6.13) двойное векторное произведение, найдем для момента импульса:
Спроектируем равенство (6.14) на оси координат. Для проектирования следует выбрать подвижные оси координат, которые жестко связаны с твердым телом. Проекция на ось ох имеет вид и может быть записана в форме с коэффициентами
Аналогичным образом получаются проекции на оси оу и ог. Все три проекции можно записать в виде Здесь индексы i, j задают номер координатной оси. Величины
Если твердое тело является сплошным, а не состоит из отдельных материальных точек, то суммы в (6.19) заменяются интегралами но объему твердого тела. Например, компонента -
Выразим теперь через тензор инерции кинетическую энергию вращения твердого тела. В системе отсчета центра инерции имеем
Подставляя в формулу (6.21) выражения для проекций момента импульса из (6.18), получим для кинетической энергии твердого тела следующую формулу:
Тензор инерции определяется распределением масс в твердом теле и является характеристикой твердого тела, не зависящей от характера движения твердого тела. Диагональные компоненты тензора инерции равны моментам инерции при вращении твердого тела вокруг осей, совпадающих с координатными осями подвижной системы координат. Недиагональные компоненты тензора инерции называются центробежными моментами инерции. Так как тензор инерции является симметричным тензором второго ранга, то преобразованием координат его можно привести к диагональной форме, когда недиагональные компоненты будут равны нулю. Оси декартовой системы координат, в которой тензор инерции имеет диагональную форму, называются главными осями инерции. Диагональные компоненты тензора инерции в главных осях инерции называются главными моментами инерции а обычно записываются с одним индексом: I 1, I 2, I 3. В главных осях инерции момент импульса и кинетическая энергия твердого тела записываются в особенно простой форме:
Если твердое тело обладает некоторой симметрией, то направления главных осей инерции совпадают с осями симметрии твердого тела. Поэтому при вычислении тензора инерции для таких твердых тел оси координат направляют по осям симметрии твердого тела.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.14.104 (0.006 с.) |

 Твердое тело в классической механике определяется как система материальных точек, расстояние между которыми не изменяется. Это может быть система из отдельных материальных точек, соединенных жесткими стержнями, или сплошное тело. Положение твердого тела относительно некоторой системы координат XYZ можно задать следующим образом (рис. 6.1). С твердым телом жестко связывается декартова система координат xyz, которую в дальнейшем будем называть подвижной системой координат. Координаты начала подвижной системы координат задаются вектором
Твердое тело в классической механике определяется как система материальных точек, расстояние между которыми не изменяется. Это может быть система из отдельных материальных точек, соединенных жесткими стержнями, или сплошное тело. Положение твердого тела относительно некоторой системы координат XYZ можно задать следующим образом (рис. 6.1). С твердым телом жестко связывается декартова система координат xyz, которую в дальнейшем будем называть подвижной системой координат. Координаты начала подвижной системы координат задаются вектором  . Ориентацию подвижной системы координат относительно неподвижной системы координат обычно задают с помощью углов Эйлера. Для определения углов Эйлера совместим начала подвижной и неподвижной систем координат (рис. 6.2).
. Ориентацию подвижной системы координат относительно неподвижной системы координат обычно задают с помощью углов Эйлера. Для определения углов Эйлера совместим начала подвижной и неподвижной систем координат (рис. 6.2).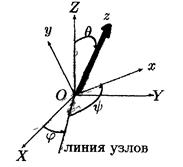 Один из углов Эйлера — это угол Θ между осями OZ и oz, отсчитываемый от оси OZ. Линия пересечения плоскостей 'XOY и хоу называется линией узлов. Второй угол Эйлера φ — это угол между осью ОХ и линией узлов. Третий угол Эйлера φ отсчитывается в плоскости хоу от линии узлов до оси ох. Три угла Эйлера полностью определяют ориентацию подвижной системы координат относительно неподвижной. Задание трех координат подвижного начала координат и трех углов Эйлера полностью определяет положение твердого тела. Поэтому твердое тело имеет шесть степеней свободы.
Один из углов Эйлера — это угол Θ между осями OZ и oz, отсчитываемый от оси OZ. Линия пересечения плоскостей 'XOY и хоу называется линией узлов. Второй угол Эйлера φ — это угол между осью ОХ и линией узлов. Третий угол Эйлера φ отсчитывается в плоскости хоу от линии узлов до оси ох. Три угла Эйлера полностью определяют ориентацию подвижной системы координат относительно неподвижной. Задание трех координат подвижного начала координат и трех углов Эйлера полностью определяет положение твердого тела. Поэтому твердое тело имеет шесть степеней свободы.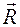 , так и с помощью радиуса-вектора
, так и с помощью радиуса-вектора  , относительно подвижной системы координат (рис. 6.1). Из рис. 6.1 видно, что
, относительно подвижной системы координат (рис. 6.1). Из рис. 6.1 видно, что  . (6.1)
. (6.1) . (6.2)
. (6.2) — скорость подвижного начала координат. Так как вектор
— скорость подвижного начала координат. Так как вектор 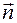 , а угол поворота при вращении вокруг нее обозначим через Ф. Тогда, используя формулу для уравнения Лагранжа, используя определение обобщенного импульса
, а угол поворота при вращении вокруг нее обозначим через Ф. Тогда, используя формулу для уравнения Лагранжа, используя определение обобщенного импульса 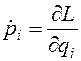 , производную от
, производную от 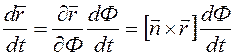 (6.3) Введем вектор мгновенной угловой скорости
(6.3) Введем вектор мгновенной угловой скорости 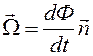 (6.4) Вектор угловой скорости направлен по оси вращения и связан с направлением вращения правилом правого буравчика, С учетом сделанных определений скорость произвольной точки твердого тела можно представить в виде суммы скорости подвижного начала координат и скорости, обусловленной вращением тела:
(6.4) Вектор угловой скорости направлен по оси вращения и связан с направлением вращения правилом правого буравчика, С учетом сделанных определений скорость произвольной точки твердого тела можно представить в виде суммы скорости подвижного начала координат и скорости, обусловленной вращением тела: 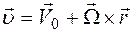 (6.5)
(6.5) , как показано на рис. 6.3. Из рисунка и формулы (6.5) получим новое выражение для скорости:
, как показано на рис. 6.3. Из рисунка и формулы (6.5) получим новое выражение для скорости: ,
,  . (6.6)
. (6.6)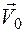 — скорость нового начала подвижной с-мы координат,
— скорость нового начала подвижной с-мы координат,  — координата точки тв. тела относительно новой подвижной с-мы координат. Последнее равенство в (6.6) аналогично равенству в формуле (6.5) с той же самой угловой скоростью
— координата точки тв. тела относительно новой подвижной с-мы координат. Последнее равенство в (6.6) аналогично равенству в формуле (6.5) с той же самой угловой скоростью  , что доказывает утверждение о независимости угловой скорости от выбора начала подвижной с-мы координат. Поэтому можно говорить об угловой скорости вращения тв. тела без указания где выбрано начало подвижной с-мы коорд.
, что доказывает утверждение о независимости угловой скорости от выбора начала подвижной с-мы координат. Поэтому можно говорить об угловой скорости вращения тв. тела без указания где выбрано начало подвижной с-мы коорд. Рис. 6.З Как и другие векторы, векторы угловой скорости можно складывать. Запишем сумму трех угловых скоростей, каждая из которых получается при изменении только одного из углов Эйлера. В результате получим
Рис. 6.З Как и другие векторы, векторы угловой скорости можно складывать. Запишем сумму трех угловых скоростей, каждая из которых получается при изменении только одного из углов Эйлера. В результате получим  , (6.7)
, (6.7) и
и 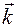 — это единичные векторы, направленные соответственно вдоль осей OZ и oz, вокруг которых происходит вращение при изменении углов φ и ψ. Единичный вектор
— это единичные векторы, направленные соответственно вдоль осей OZ и oz, вокруг которых происходит вращение при изменении углов φ и ψ. Единичный вектор  направлен вдоль линии узлов, которая является осью вращения при изменении угла
направлен вдоль линии узлов, которая является осью вращения при изменении угла 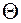 . Формула (6.7) дает разложение вектора угловой скорости по трем направлениям, которые не совпадают с направлениями координатных осей. Спроектируем векторы
. Формула (6.7) дает разложение вектора угловой скорости по трем направлениям, которые не совпадают с направлениями координатных осей. Спроектируем векторы 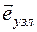 на подвижные оси, что дает
на подвижные оси, что дает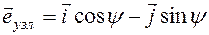 , (6.8)
, (6.8)  . (6.9) Подставляя разложения (6.8) и (6.9) в формулу (6.7) и собирая коэффициенты при одинаковых базисных векторах, получим проекции вектора угловойскорости наподвижные оси:
. (6.9) Подставляя разложения (6.8) и (6.9) в формулу (6.7) и собирая коэффициенты при одинаковых базисных векторах, получим проекции вектора угловойскорости наподвижные оси:  ,
,  ,
, . (6.10) - кинематическими формулами Эйлера. Они позволяют найти вектор угловой скорости, если задан закон изменения углов Эйлера как функция времени. Аналогичным образом после проектирования векторов
. (6.10) - кинематическими формулами Эйлера. Они позволяют найти вектор угловой скорости, если задан закон изменения углов Эйлера как функция времени. Аналогичным образом после проектирования векторов 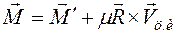 и кинетическую энергию
и кинетическую энергию 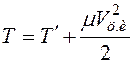 твердого тела. Их можно представить в виде
твердого тела. Их можно представить в виде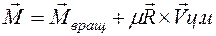 , (6.11)
, (6.11)  . (6.12)
. (6.12) и
и  — момент импульса и кинетическая энергия твердого тела в системе отсчета центра инерции твердого тела. В системе отсчета центра инерции твердое тело может только вращаться. Поэтому момент импульса и кинетическая энергия связаны только с вращением и должны выражаться через угловую скорость твердого тела. Начало подвижной системы координат поместим в центр инерции твердого тела и перейдем в систему отсчета центра инерции. Подставляя скорость
— момент импульса и кинетическая энергия твердого тела в системе отсчета центра инерции твердого тела. В системе отсчета центра инерции твердое тело может только вращаться. Поэтому момент импульса и кинетическая энергия связаны только с вращением и должны выражаться через угловую скорость твердого тела. Начало подвижной системы координат поместим в центр инерции твердого тела и перейдем в систему отсчета центра инерции. Подставляя скорость  . (6.13)
. (6.13) . (6.14)
. (6.14) (6.15)
(6.15)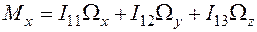 (6.16)
(6.16)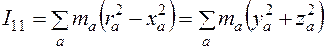 ,
, ,
,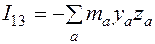 .
.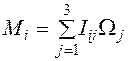 . (6.18)
. (6.18) являются компонентами симметричного тензора второго ранга, называемого тензором инерции. Компоненты тензора инерции записываются в виде следующей симметричной матрицы:
являются компонентами симметричного тензора второго ранга, называемого тензором инерции. Компоненты тензора инерции записываются в виде следующей симметричной матрицы: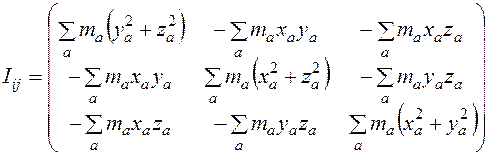 (6.19)
(6.19)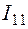 тензора инерции вычисляется по формуле
тензора инерции вычисляется по формуле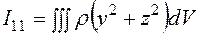 . (6.20)
. (6.20) . (6.21)
. (6.21)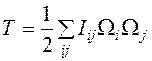 . (6.22)
. (6.22)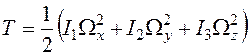 , (6.23)
, (6.23)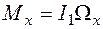 ,
,  ,
,  . (6.24)
. (6.24)


