
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Импульс, з-н изменения импульса с-мы материальных точек.Содержание книги
Поиск на нашем сайте
Импульс, з-н изменения импульса с-мы материальных точек. Закон 2 Ньютона. Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. Второй закон Ньютона связывает ускорение тела с действующей на него силой:
Так как масса — величина постоянная, то уравнение (1.1) можно записать в форме Величина Изменение импульса материальной точки вызывается действием на нее силы. В уравнении (1.7) введено общепринятое в классической механике обозначение, когда полная производная по времени обозначается точкой над буквой. Несколько тел, каждое из которых можно рассматривать как материальную точку, составляют систему материальных точек. Для каждой материальной точки можно записать уравнение второго закона Ньютона
В уравнении (1.13) индексы Из уравнений (1.13) вытекают несколько важных законов. Если просуммируем их по всем материальным точкам системы, то получим
Величина называется импульсом системы материальных точек. Импульс системы материальных точек равен сумме импульсов отдельных материальных точек. В уравнении (1.14) двойная сумма для внутренних сил обращается в нуль. Для каждой пары материальных точек в нее входят силы, которые по третьему закону Ньютона (Закон 3. Действию всегда есть равное и противоположное противодействие; иначе — взаимодействия двух тел друг с другом равны и направлены в противоположные стороны.) равны и противоположно направлены. Для каждой пары векторная сумма этих сил обращается в нуль. Поэтому равна нулю и сумма для всех сил. В результате получим
Уравнение (1.16) выражает закон изменения импульса системы материальных точек. Изменение импульса системы материальных точек вызывается только внешними силами. Если на систему не действуют внешние силы, то импульс системы материальных точек сохраняется. Систему материальных точек, на которую не действуют внешние силы, называют изолированной, или замкнутой, системой материальных точек.
Принцип Гамильтона Использование принципа Даламбера позволяет не учитывать силы реакции связей и дает возможность применять произвольные обобщенные координаты. Однако, получение уравнений в обобщенных координатах может представлять трудности из-за наличия в принципе Даламбера Рассмотрим случай, когда силы имеют потенциал. Тогда виртуальная работа сил запишется в форме В общем случае потенциальная энергия может зависеть от времени. Поскольку вариация вычисляется при фиксированном
По аналогии с выражениями (1.12) частные производные от потенциальной энергии по обобщенным координатам называют обобщенными силами:
Для того чтобы преобразовать слагаемые с ускорениями к вариации от скалярной функции, предварительно проинтегрируем уравнение В сумме, содержащей ускорения, рассмотрим одно слагаемое, например
Будем считать, что начальное в момент времени
Такие же преобразования можно произвести для всех координат всех материальных точек. Учтем еще выражение (2.14) виртуальной работы через потенциальную функцию. В результате для интеграла (2.17) получим
Время может и не входить в функцию Лагранжа. Интеграл из (2.20) обозначается буквой После введения этих обозначений условие (2.20) принимает вид Вариация действия равна нулю. Это означает, что действие имеет экстремум, принимает наибольшее или наименьшее значение, если в интеграл (2.22) в качестве зависимости Теперь можно сформулировать интегральный принцип, называемый принципом Гамильтона: Движение механической системы за конечный промежуток времени от Для консервативных систем принцип Гамильтона эквивалентен законам Ньютона. Поэтому он может считаться основным принципом механики, из которого выводятся все уравнения механики.. Это — вариационный принцип, так как зависимость обобщенных координат от времени
8. Получение уравнений Лагранжа из принципа Гамильтона. Из принципа Гамильтона обычным методом вариационного исчисления можно получить дифференциальные уравнения. Наряду с зависимостью
Это уже было отмечено ранее, что дифференцирование по времени и варьирование можно переставлять. Вариации координат рассматриваются такими, что в моменты времени Действие для пробных функций Интеграл от одного из слагаемых первой суммы в (3.5) вычислим по частям:
Согласно условию (3.4), на пределах интегрирования
Поскольку вариации координат Несмотря на то, что функция Лагранжа равна разности кинетической и потенциальной энергии, в выборе функции Лагранжа имеется некоторый произвол. Две функции Лагранжа, отличающиеся на полную производную по времени от произвольной функции координат и времени, дают одни и те же уравнения движения. Покажем это. Пусть Тогда для разности действий, отвечающих этим функциям Лагранжа, получим:
Вследствие того, что вариация координат на пределах интегрирования Ур-ия Лагранжа обобщаются на механические системы, в которых действуют непотенциальные силы. Выражение для; обо6щенной непотенциалыюй силы нужно добавить в правую часть уравнений Лагранжа. Они тогда принимают вид В частном случае, когда непотенциальные силы являются силами трения, пропорциональными первой степени скорости, они могyт быть получены из диссипативной функции Рэлея:
Циклические координаты. Для одной материальной точки производные от функции Лагранжа по
В обобщенных координатах вводится понятие обобщенного импуль са. Обобщенный импульс, сопряженный координате Если координаты не декартовы, то обобщенные импульсы больше не равны проекциям импульса. Их можно выразить через импульсы отдельных материальных точек, составляющих систему материальных точек. Рассмотрим функцию Лагранжа как сложную функцию обобщенных координат и обобщенных скоростей:
Вычислим производные по обобщенным координатам как производные от сложной функции:
Для частных производных от векторов скорости из формулы (2.4) находим, что
В рез-те имеем следующую связь обобщенного импульса с импульсами отдельных материальных точек механической системы: Обобщенный импульс, сопряженный декартовой координате, равен проекции импульса на декартову oсь. Обобщенный импульс, сопряженный угловой координате, равен проекции момента импульса на ось вращения. Чтобы убедиться в этом, выразим радиус-вектор материальной точки через сферические координаты:
Используя представление (3.32), легко проверить,
Подставляя выражение (3.33) в формулу (3.31), найдем для одной материальной точки то есть обобщенный импульс Используя определение обобщенного импульса, уравнения Лагранжа можно записать в форме Возможны случаи, когда некоторые координаты не входят в функцию Лагранжа, но в ней присутствуют их производные по времени — обобщенные скорости. Такие координаты называются циклическими координатами. Например, если в функции Лагранжа материальной точки (массой
Так как обобщенный импульс, сопряженный циклической координате, остается постоянным при движении механической системы, то говорят, что он сохраняется. Каждой циклической координате отвечает свой закон сохранения. Наличие законов сохранения упрощает решение задач механики. Уравнения Лагранжа — это дифференциальные уравнения второго порядка относительно неизвестных координат Обобщенная энергия Найдем полную производную от функции Лагранжа по времени. Так как функция Лагранжа зависит от обобщенных координат и обобщенных скоростей, которые сами являются функциями времени, то получим выражение
Воспользуемся формулой Лейбница для дифференцирования произведения двух функций и получим из нее следующее равенство:
С помощью этого равенств преобразуем выражение (3.37) и запишем его в форме
Сумма в правой части выражения (3.38) равна нулю вследствие выполнения уравнений Лагранжа
Равенство (3.38) дает полную производную от обобщенной энергии по времени
Если функция Лагранжа не зависит явно oт времени, то правая часть в формуле (3.40) равна нулю и обобщенная энергия сохраняется при движении механической системы. Для обычных механических систем при условии, что формулы преобразования к обобщенным координатам не содержат времени, функция Лагранжа дается формулой (3.26). Найдем в этом случае обобщенную энергию. Для обобщенных импульсов получим
Подставляя этот результат в формулу (3.39), найдем
то есть определение обобщенной энергии в этом случае совпадает с обычным определением механической энергии. Если на механическую систему действую силы, не имеющие потенциала, то в правой части уравнений Лагранжа стоит уже не нуль. Поэтому сумма в правой части формулы (3.38) не равна нулю, и механическая энергия не будет сохраняться даже при отсутствии явной зависимости от времени в функции Лагранжа. В частности, если непотенциальные силы являются силами трения, описываемыми диссипативной функцией Рэлея, то уменьшение механической энергии дается формулой Формула (3.43) получается из соотношения (3.38) при подстановке в него уравнения (3.12). Для механических систем, в которых силы трения могут быть описаны диссипативной функцией Рэлея, уравнения Лагранжа имеют вид
Движение в центральном поле Вследствие сферической симметрии поля сохраняется вектор момента импульса
Координата
Согласно формуле (3.34) обобщенный импульс для одной материальной точки
Этот обобщенный импульс равен проекции момента импульса материальной точки на ось OZ. Будем считать, что постоянная М положительна, что соответствует выбору положительного направления оси OZ по положительному направлению вектора момента импульса. В этом случае всегда
Из формул (4.9) и (4.10) находим скорость изменения площади с течением времени. Эта величина называется секторной скоростью и в центральном поле
За равные промежутки времени радиус-вектор материальной точки заметает одинаковые площади. Это утверждение, известное как закон площадей, является другой формулировкой закона сохранения момента импульса. Закон площадей выполняется для любого центрального поля. Так как функция Лагранжа материальной точки в центральном поле не зависит явно от времени, то сохраняется энергия материальной точки. В полярных координатах выражение для энергии записывается в форме
Из выражения (4.9) найдем производную
где введено понятие эффективной потенциальной энергии
Формула (4.13) для энергии совпадает с формулой для энергии материальной точки, движущейся по радиусу и находящейся в потенциальном поле с эффективной потенциальной энергией
Разделяя в выражении (4.15) переменные и интегрируя его, получим неявную зависимость
Выражение (4.15) и интеграл (4.16) имеют смысл только тогда, когда подкоренное выражение не отрицательно, то есть когда выполняется неравенство Найдем теперь уравнение траектории. Так как производные
Интегрируя выражение (4.17), находим уравнение траектории в полярных координатах:
Интеграл можно вычислить только после задания потенциальной энергии
Рис. 4.3 Рис. 4.4 Примеры возможных траекторий приведены на рис. 4.3 и рис. 4.4. Угол
Если при сложении нескольких
где Задача Кеплера Рассмотрим важный случай центрального поля, когда потенциальная энергия равна Ур-ие траектории получим, вычисляя интеграл (4.18). Запишем его для поля притяжения, выбирая знак минус в (4.21). Положим также постоянную
где введены две новые постоянные: параметр
Материальная точка, движущаяся по гиперболе, может уйти на бесконечность и будет иметь там ненулевую скорость. При
Размер большой полуоси эллипса не зависит от момента импульса материальной точки и определяется только ее энергией. Период обращения материальной точки вокруг центра найдем путем интегрирования соотношения (4.11) закона площадей. За период обращения вокруг центра площадь, заметаемая радиусом-вектором материальной точки, равна площади эллипса. Используя значения для
Для планет Солнечной системы отношение Закон 1. Планета движется по эллипсу, в одном из фокусов которого находится Солнце. Закон 2. Площади, заметаемые радиусом-вектором планеты за одинаковые промежутки времени, равны. Закон 3. Квадраты периодов обращения планет относятся как кубы их больших полуосей. Уравнение траектории для поля отталкивания, когда | ||
|
| Поделиться: |

 (1.1)
(1.1) (1.6)
(1.6) называется импульсом, или количеством движения материальной точки. Используя определение импульса, второй закон Ньютона записываем в форме
называется импульсом, или количеством движения материальной точки. Используя определение импульса, второй закон Ньютона записываем в форме  (1.7)
(1.7) (1.13)
(1.13) дают номер материальной точки. Действующие на материальную точку силы разделены на внешние
дают номер материальной точки. Действующие на материальную точку силы разделены на внешние  и внутренние
и внутренние  . Внешние силы — это силы, действующие со стороны тел, не входящих в систему материальных точек. Внутренние силы — это силы, действующие на материальную точку со стороны других тел, составляющих систему материальных точек. Здесь
. Внешние силы — это силы, действующие со стороны тел, не входящих в систему материальных точек. Внутренние силы — это силы, действующие на материальную точку со стороны других тел, составляющих систему материальных точек. Здесь  — сила, действующая на материальную точку, индекс которой
— сила, действующая на материальную точку, индекс которой  , со стороны материальной точки с номером
, со стороны материальной точки с номером  .
. (1.14)
(1.14) (1.15)
(1.15) (1.16)
(1.16) (2.13) скалярных произведений. С помощью преобразований координат уравнения (2.13) можно преобразовать к виду, содержащему только скалярные функции обобщенных координат. Мы укажем другой путь, когда вначале от принципа Даламбера переходят к интегральному вариационному принципу. Получение уравнений механики из вариационного принципа позволило получить много важных результатов. В дальнейшем вариационные принципы стали использовать и в других областях теоретической физики.
(2.13) скалярных произведений. С помощью преобразований координат уравнения (2.13) можно преобразовать к виду, содержащему только скалярные функции обобщенных координат. Мы укажем другой путь, когда вначале от принципа Даламбера переходят к интегральному вариационному принципу. Получение уравнений механики из вариационного принципа позволило получить много важных результатов. В дальнейшем вариационные принципы стали использовать и в других областях теоретической физики. (2.14)
(2.14) , это никак не сказывается на выводах. При использовании обобщенных координат потенциальная энергия в конечном счете является функцией обобщенных координат. Тогда вариация потенциальной энергии будет иметь вид
, это никак не сказывается на выводах. При использовании обобщенных координат потенциальная энергия в конечном счете является функцией обобщенных координат. Тогда вариация потенциальной энергии будет иметь вид (2.15)
(2.15) (2.16)
(2.16) (2.9) по времени:
(2.9) по времени:  . (2.17)
. (2.17) . Индекс
. Индекс  (2.18)
(2.18) и конечное в момент времени
и конечное в момент времени  положения системы материальных точек заданы. Поэтому
положения системы материальных точек заданы. Поэтому  для этих моментов времени равно нулю, и первое слагаемое в (2.18) обращается в нуль. Так как вариации координат рассматриваются для фиксированных моментов времени, то производную по времени и варьирование можно переставить местами. Второе слагаемое в (2.18) преобразуется к виду
для этих моментов времени равно нулю, и первое слагаемое в (2.18) обращается в нуль. Так как вариации координат рассматриваются для фиксированных моментов времени, то производную по времени и варьирование можно переставить местами. Второе слагаемое в (2.18) преобразуется к виду (2.19)
(2.19) . (2.20) Разность кинетической и потенциальной энергии, которая входит в последний из интегралов в формуле (2.20), называется функцией Лагранжа и обозначается буквой
. (2.20) Разность кинетической и потенциальной энергии, которая входит в последний из интегралов в формуле (2.20), называется функцией Лагранжа и обозначается буквой  . Функция Лагранжа зависит от координат и скоростей материальных точек. При переходе к обобщенным координатам она выражается через обобщенные координаты и обобщенные скорости:
. Функция Лагранжа зависит от координат и скоростей материальных точек. При переходе к обобщенным координатам она выражается через обобщенные координаты и обобщенные скорости: (2.21)
(2.21) и называется действием;
и называется действием;  (2.22)
(2.22) . (2.23)
. (2.23) подставить функции, описывающие движение механической системы. Поэтому условие экстремума действия можно использовать для отыскания закона движения системы материальных точек.
подставить функции, описывающие движение механической системы. Поэтому условие экстремума действия можно использовать для отыскания закона движения системы материальных точек. , отличающиеся от
, отличающиеся от  (3.1) Дифференцируя равенство (3.1) по времени, найдем
(3.1) Дифференцируя равенство (3.1) по времени, найдем  (3.2) Откуда следует, что вариация скорости равна производной от вариации координаты:
(3.2) Откуда следует, что вариация скорости равна производной от вариации координаты:  . (3.3).
. (3.3). (3.4)
(3.4) разложим в ряд в линейном приближении по
разложим в ряд в линейном приближении по  , и
, и  :
:  (3.5)
(3.5) (3.6)
(3.6) . Поэтому первое слагаемое в последнем равенстве обращается в нуль. Подставляя теперь результат из (3.6) в (3.5) и записывая вариацию действия, получим
. Поэтому первое слагаемое в последнем равенстве обращается в нуль. Подставляя теперь результат из (3.6) в (3.5) и записывая вариацию действия, получим (3.7)
(3.7) . В результате получается система дифференциальных уравнений, которые в механике называются уравнениями Лагранжа:
. В результате получается система дифференциальных уравнений, которые в механике называются уравнениями Лагранжа: 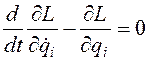 (3.8) Уравнения Лагранжа - это система дифференциальных уравнений относительно неизвестных обобщенных координат
(3.8) Уравнения Лагранжа - это система дифференциальных уравнений относительно неизвестных обобщенных координат  отличаются на полную производную по времени от некоторой функции
отличаются на полную производную по времени от некоторой функции  ;
; 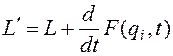 (3.9)
(3.9)
 равны. Поэтому онибудут обращаться в нуль одними и теми же зависимостями
равны. Поэтому онибудут обращаться в нуль одними и теми же зависимостями 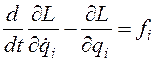 , где
, где  (3,10)
(3,10) ;
;  (3.11) Коэффициенты
(3.11) Коэффициенты  могут зависеть от координат и характеризуют силы трения в механической системе. Для механических систем, в которых силы трения могут быть описаны диссипативной функцией Рэлея, уравнения Лагранжа имеют вид
могут зависеть от координат и характеризуют силы трения в механической системе. Для механических систем, в которых силы трения могут быть описаны диссипативной функцией Рэлея, уравнения Лагранжа имеют вид  (3.12) Ур-ия (3.10) и (3.12) не могут быть получены на основе вариационного принципа. Они выводятся непосредственно из принципа Даламбера. В лагранжевом формализме можно включать в уравнения движения силы немеханической природы. Например, ур-ия движения заряда
(3.12) Ур-ия (3.10) и (3.12) не могут быть получены на основе вариационного принципа. Они выводятся непосредственно из принципа Даламбера. В лагранжевом формализме можно включать в уравнения движения силы немеханической природы. Например, ур-ия движения заряда  в электромагнитном поле получаются из фунции Лагранжа, которая содержит слагаемые, описывающие взаимодействие заряда с полем:
в электромагнитном поле получаются из фунции Лагранжа, которая содержит слагаемые, описывающие взаимодействие заряда с полем:  (3.13) где
(3.13) где  и
и  — скалярный и векторный потенциалы электромагнитного поля,
— скалярный и векторный потенциалы электромагнитного поля,  — скорость света в вакууме. Электромагнитные величины записаны в гауссовой системе единиц. При замене функции Лагранжа классической механики на функцию Лагранжа специальной теории относительности ур-ия Лагранжа дают ур-ия движения механики спец. теории относительности.
— скорость света в вакууме. Электромагнитные величины записаны в гауссовой системе единиц. При замене функции Лагранжа классической механики на функцию Лагранжа специальной теории относительности ур-ия Лагранжа дают ур-ия движения механики спец. теории относительности. равны проекциям импульса на декартовы оси
равны проекциям импульса на декартовы оси ;
;  ;
;  (3.27)
(3.27) определяется по формуле, аналогичной формулам (3.27):
определяется по формуле, аналогичной формулам (3.27):  (3.28)
(3.28)
 (3.29)
(3.29)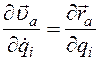 (3.30)
(3.30) (3.31)
(3.31) (3.32)
(3.32) (3.33)
(3.33)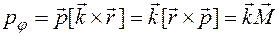 , (3.34)
, (3.34) , сопряженный угловой координате
, сопряженный угловой координате 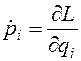 (3.35)
(3.35) , находящейся в потенциальном поле
, находящейся в потенциальном поле  :
:  (3.14) потенциальная энергия не будет зависеть от координат х и у, то координаты х и у будут циклическими. Для циклической координаты правая часть уравнения (3.35) равна нулю и, следовательно, интеграл этого уравнения имеет вид
(3.14) потенциальная энергия не будет зависеть от координат х и у, то координаты х и у будут циклическими. Для циклической координаты правая часть уравнения (3.35) равна нулю и, следовательно, интеграл этого уравнения имеет вид . (3.36)
. (3.36) (3.37)
(3.37)

 (3.38)
(3.38) :
: (3.39).
(3.39). (3.40)
(3.40) (3.41)
(3.41) (3.42)
(3.42) (3.43)
(3.43) , определенный относительно центра поля. Так как
, определенный относительно центра поля. Так как  , то векторы
, то векторы  и
и  перпендикулярны постоянному вектору
перпендикулярны постоянному вектору  (4.8)
(4.8) (4.9)
(4.9)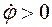 и, следовательно, материальная точка в центральном поле движется так, что угол
и, следовательно, материальная точка в центральном поле движется так, что угол  Закон сохранения (4.9) часто формулируется как закон площадей. Рассмотрим два положения материальной точки на траектории в два бесконечно близких момента времени, как показано на рис. 4.1. Из рисунка видно, что площадь бесконечно малого сектора, ограниченного двумя положениями радиуса-вектора и участком траектории, равна
Закон сохранения (4.9) часто формулируется как закон площадей. Рассмотрим два положения материальной точки на траектории в два бесконечно близких момента времени, как показано на рис. 4.1. Из рисунка видно, что площадь бесконечно малого сектора, ограниченного двумя положениями радиуса-вектора и участком траектории, равна . (4.10)
. (4.10) (4.11)
(4.11) (4.12)
(4.12) и подставим ее в формулу (4.12). В результате получим
и подставим ее в формулу (4.12). В результате получим (4.13)
(4.13) , равной
, равной (4.14)
(4.14) . Из соотношения (4.13) находим, что
. Из соотношения (4.13) находим, что (4.15)
(4.15) :
:
 (4.16)
(4.16) ). Исследование этого неравенства позволяет, не вычисляя интеграла, определить области пространства, в которых возможно движение материальной точки при заданных энергии
). Исследование этого неравенства позволяет, не вычисляя интеграла, определить области пространства, в которых возможно движение материальной точки при заданных энергии  . Качественно такое исследование можно провести графическим путем, если построить график зависимости
. Качественно такое исследование можно провести графическим путем, если построить график зависимости  . Пример такого построения приведен на рис.. На этом графике условия неравенства
. Пример такого построения приведен на рис.. На этом графике условия неравенства  . Следовательно, при обращении вокруг центра поля материальная точка будет то приближаться к центру на расстояние
. Следовательно, при обращении вокруг центра поля материальная точка будет то приближаться к центру на расстояние  , то удаляться от него на расстояние
, то удаляться от него на расстояние  .
. и
и  (4.17)
(4.17) (4.18)
(4.18) . Если положить
. Если положить  , то изменение знака
, то изменение знака  и где, следовательно, материальная точка находится на минимальном или максимальном удалении от центра поля. Точки минимального или максимального удаления материальной точки от центра поля называются точками поворота. Таким образом при
и где, следовательно, материальная точка находится на минимальном или максимальном удалении от центра поля. Точки минимального или максимального удаления материальной точки от центра поля называются точками поворота. Таким образом при  начало отсчета угла
начало отсчета угла  , лежащим по разные стороны от точки поворота, отвечают одинаковые абсолютные значения угла
, лежащим по разные стороны от точки поворота, отвечают одинаковые абсолютные значения угла  и
и  .
.

 между положениями
между положениями  (4.19)
(4.19) , то материальная точка возвратится на уже пройденный участок траектории и сама траектория будет замкнутой кривой. Условие замкнутости траектории записывается в форме
, то материальная точка возвратится на уже пройденный участок траектории и сама траектория будет замкнутой кривой. Условие замкнутости траектории записывается в форме (4.20)
(4.20) — целые числа. Если это условие не выполняется, то траектория будет незамкнутой кривой, расположенной в кольце между окружностями с радиусами
— целые числа. Если это условие не выполняется, то траектория будет незамкнутой кривой, расположенной в кольце между окружностями с радиусами  (4.21) Силу, действующую на материальную точку, найдем по формуле
(4.21) Силу, действующую на материальную точку, найдем по формуле 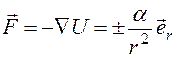 (4,22), где
(4,22), где  — единичный вектор, направленный по радиусу. Знак плюс относится к полю отталкивания, когда сила направлена от центра. Знак минус - полю притяжения. Для рассматриваемого потенциального поля сила обратно пропорциональна квадрату радиуса. Такую зависимость силы от расстояния имеют поле тяготения сферически симметричной массы и электрическое поле точечн. или сферически симметричн. заряда.
— единичный вектор, направленный по радиусу. Знак плюс относится к полю отталкивания, когда сила направлена от центра. Знак минус - полю притяжения. Для рассматриваемого потенциального поля сила обратно пропорциональна квадрату радиуса. Такую зависимость силы от расстояния имеют поле тяготения сферически симметричной массы и электрическое поле точечн. или сферически симметричн. заряда. =0 и выберем знак плюс перед интегралом. Такой выбор постоянной и знака перед интегралом соответствует выбору оси ОХ в направлении на положение минимального удаления материальной точки от центра. Тогда интеграл имеет вид
=0 и выберем знак плюс перед интегралом. Такой выбор постоянной и знака перед интегралом соответствует выбору оси ОХ в направлении на положение минимального удаления материальной точки от центра. Тогда интеграл имеет вид (4.23) Интеграл (4.23) приводится к табличному интегралу путем замены
(4.23) Интеграл (4.23) приводится к табличному интегралу путем замены  и выделением полного квадрата под знаком корня. Результат интегрирования можно записать в форме
и выделением полного квадрата под знаком корня. Результат интегрирования можно записать в форме  (4.24)
(4.24) и эксцентриситет
и эксцентриситет  ;
;  (4.25) Уравнение (4.24) задает в полярных координатах одно из конических сечений: гиперболу, параболу или эллипс. Начало полярной системы координат совпадает с одним из фокусов гиперболы или эллипса или с фокусом параболы. Вид конического сечения зависит от величины эксцентриситета
(4.25) Уравнение (4.24) задает в полярных координатах одно из конических сечений: гиперболу, параболу или эллипс. Начало полярной системы координат совпадает с одним из фокусов гиперболы или эллипса или с фокусом параболы. Вид конического сечения зависит от величины эксцентриситета  уравнение задает гиперболу. В этом случае положительна энергия материальной точки:
уравнение задает гиперболу. В этом случае положительна энергия материальной точки:  (4.26)
(4.26) второе слагаемое в (4.26) обращается в 0 и энергия материальной точки равна ее кинетической энергии
второе слагаемое в (4.26) обращается в 0 и энергия материальной точки равна ее кинетической энергии  . Если
. Если  , то эксцентриситет
, то эксцентриситет  и уравнение (4.24) задает параболу. Материальная точка по-прежнему может уйти на бесконечность, но скорость ее на бесконечности =0. И наконец, при отрицательной энергии
и уравнение (4.24) задает параболу. Материальная точка по-прежнему может уйти на бесконечность, но скорость ее на бесконечности =0. И наконец, при отрицательной энергии  . Тогда уравнение (4.24) описывает эллипс. Движение материальной точки ограничено областью вблизи центра поля.
. Тогда уравнение (4.24) описывает эллипс. Движение материальной точки ограничено областью вблизи центра поля. Если пренебречь взаимодействием планет между собой, то полученные для поля притяжения с
Если пренебречь взаимодействием планет между собой, то полученные для поля притяжения с  результаты можно применить к описанию движения планет Солнечной системы. Так как масса Солнца
результаты можно применить к описанию движения планет Солнечной системы. Так как масса Солнца  >> массы планет Солнечной системы, то центр поля можно считать совпадающим с центром Солнца, а приведенную массу считать = массе планеты. Из з-на всемирного тяготения имеем
>> массы планет Солнечной системы, то центр поля можно считать совпадающим с центром Солнца, а приведенную массу считать = массе планеты. Из з-на всемирного тяготения имеем  . Выразим измеряемые астрономами величины — большую полуось орбиты и период обращения планеты — через энергию и момент импульса планеты. Из рис. 4.5 траектории планеты видно, что
. Выразим измеряемые астрономами величины — большую полуось орбиты и период обращения планеты — через энергию и момент импульса планеты. Из рис. 4.5 траектории планеты видно, что ;
;  (4.27)
(4.27) для площади эллипса и закон площадей (4.11), получим
для площади эллипса и закон площадей (4.11), получим (4.28) Подставляя в (4.28) значения
(4.28) Подставляя в (4.28) значения 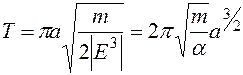 (4.29)
(4.29)

 . Lля них период обращения зависит только от величины большой полуоси орбиты. Эти рез-ты для движения материальной точки по эллипсу в центральном поле в приложении к движению планет Солнечной системы открыты Кеплером. Законы Кеплера
. Lля них период обращения зависит только от величины большой полуоси орбиты. Эти рез-ты для движения материальной точки по эллипсу в центральном поле в приложении к движению планет Солнечной системы открыты Кеплером. Законы Кеплера .:
.:  (4.30)
(4.30) 


