
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутренние поверхностные силы, тензор напряжений.Содержание книги
Поиск на нашем сайте Для выделенного подвижного объема сплошной среды, как для любой с-ы материальных точек, должен выполняться закон изменения импульса. На выделенный объем действуют два вида сил. Это — силы, действующие на все частицы объема, или массовые сил. и силы, действующие на поверхность объема со стороны соседних слоев сплошной среды, или поверхностные силы. Массовые силы задают при помощи плотности силы, отнесенной к единице массы. Поверхностные силы задают при помощи плотности, отнесенной к единице поверхности. Плотность массовых и плотность поверхностных сил определяются соотношениями: Подставим выражение плотности поверхностной силы через тензор напряжений (8.34) в поверхностный интеграл в формуле (8.33) и преобразуем его в объемный. Для этого воспользуемся теоремой Остроградского— Гаусса. Запишем ее вначале в индексной форме для произвольного вектора
Записывая теперь ур-ие (8.33) в проекциях на оси декартовой системы координат и преобразуя с помощью (8.36) поверхностный интеграл в объемный, получим соотношение
Запишем это ур-ие в проекциях на декартовы оси и подставим в левую часть производную от вектора Если поверхностный интеграл в правой части равенства (8.40) с помощью теоремы Остроградского — Гаусса (8.35) преобразовать к объемному, то после сокращений получится равенство Откуда следует, что В качестве дополнительных соотношений, замыкающих систему уравнений движения сплошной среды, привлекают уравнения, которые связывают напряжения в сплошной среде с ее деформацией или скоростью деформации. Выбор этих соотношений определяет модель сплошной среды, которую будут описывать уравнения. Для таких сред, как газы, жидкости, упругие тела, соответствующие модели получаются из простых предположений о связи напряжений с характеристиками сплошной среды.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 759; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 ,
,  . (8.32) Сумма сил, действующих на объем, определится суммой интегралов по объему и по поверхности от этих плотностей. Используем выражение
. (8.32) Сумма сил, действующих на объем, определится суммой интегралов по объему и по поверхности от этих плотностей. Используем выражение  для производной от импульса и запишем закон изменения импульса некоторого подвижного объема сплошной среды в виде
для производной от импульса и запишем закон изменения импульса некоторого подвижного объема сплошной среды в виде  . (8.33) Поверхностная сила
. (8.33) Поверхностная сила  , действующая на элементарную площадку
, действующая на элементарную площадку  поверхности, ограничивающей выделенный объем, в общем случае зависит от ориентации этой площадки. Ориентацию площадки задают нормалью к ней
поверхности, ограничивающей выделенный объем, в общем случае зависит от ориентации этой площадки. Ориентацию площадки задают нормалью к ней 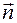 . Зависимость плотности поверхностной силы
. Зависимость плотности поверхностной силы  от ориентации площадки может быть представлена в тензорной форме:
от ориентации площадки может быть представлена в тензорной форме:  . (8.34) Здесь индексы означают номер проекции на оси декартовой системы координат. Величина
. (8.34) Здесь индексы означают номер проекции на оси декартовой системы координат. Величина  является тензором второго ранга и называется тензором напряжений. С его помощью рассчитываются поверхностные силы, действующие в любой точке сплошной среды.
является тензором второго ранга и называется тензором напряжений. С его помощью рассчитываются поверхностные силы, действующие в любой точке сплошной среды. :
: ,
,  . (8.35) По аналогии с правой частью формулы (8.35) проекции поверхностной силы преобразовываются к объемным интегралам сл. обр.:
. (8.35) По аналогии с правой частью формулы (8.35) проекции поверхностной силы преобразовываются к объемным интегралам сл. обр.:  . (8.36)
. (8.36) . (8.37) - должно выполняться для любого подвижного объема, то отсюда следует, что выражение в скобках равно нулю. Это приводит к ур-нию
. (8.37) - должно выполняться для любого подвижного объема, то отсюда следует, что выражение в скобках равно нулю. Это приводит к ур-нию  . (8.38) -выражает закон изменения импульса, записанный для каждой точки сплошной среды. Ур-ние (8.38) - уравнением движения сплошной среды. Оно связывает ускорение сплошной среды с действующими на среду силами и с напряжениями, возникающими в сплошной среде. Запишем закон изменения момента импульса для подвижного объема сплошной среды. В сумму моментов сил входят моменты массовых и поверхностных сил, которые соответственно будут задаваться объемным и поверхностным интегралами. В результате уравнение закона изменения момента импульса принимает вид
. (8.38) -выражает закон изменения импульса, записанный для каждой точки сплошной среды. Ур-ние (8.38) - уравнением движения сплошной среды. Оно связывает ускорение сплошной среды с действующими на среду силами и с напряжениями, возникающими в сплошной среде. Запишем закон изменения момента импульса для подвижного объема сплошной среды. В сумму моментов сил входят моменты массовых и поверхностных сил, которые соответственно будут задаваться объемным и поверхностным интегралами. В результате уравнение закона изменения момента импульса принимает вид  . (8.39)
. (8.39) из уравнения (8.38). Тогда интегралы, содержащие массовые силы в левых и правых частях уравнений, взаимно уничтожатся. Останутся только члены, содержащие тензор напряжений. Например, проекция ур-ия (8.39) на ось ох примет вид
из уравнения (8.38). Тогда интегралы, содержащие массовые силы в левых и правых частях уравнений, взаимно уничтожатся. Останутся только члены, содержащие тензор напряжений. Например, проекция ур-ия (8.39) на ось ох примет вид  . (8.40)
. (8.40) . (8.41)
. (8.41) . Проекции на другие оси дадут условия:
. Проекции на другие оси дадут условия:  ,
,  . Из з-на изменения момента импульса вытекает, что тензор напряжений является симметричным тензором. Вследствие симметрии он имеет только 6 независимых компонент. Так как тензор напряжений не задан и определяется в процессе решения задачи о движении сплошной среды, то число неизвестных в уравнениях (8.38) больше числа уравнений. Поэтому уравнения (8.38) должны быть дополнены. Одним из таких дополнительных уравнений является уравнение неразрывности
. Из з-на изменения момента импульса вытекает, что тензор напряжений является симметричным тензором. Вследствие симметрии он имеет только 6 независимых компонент. Так как тензор напряжений не задан и определяется в процессе решения задачи о движении сплошной среды, то число неизвестных в уравнениях (8.38) больше числа уравнений. Поэтому уравнения (8.38) должны быть дополнены. Одним из таких дополнительных уравнений является уравнение неразрывности 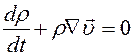 которое выполняется для любой сплошной среды.
которое выполняется для любой сплошной среды.


