
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип виртуальных перемещений и принцип ДаламбераСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В динамике связи можно учесть с помощью введения сил реакции связей. Силы реакции связей Силы реакции связей заранее неизвестны и определяются во время интегрирования уравнений движения. Поэтому при наличии связей решение задач механики с помощью уравнений второго закона Ньютона усложняется тем, что необходимо интегрировать больше уравнений, чем число степеней свободы, и тем, что приходится определять силы реакции связей. Вначале рассмотрим случай, когда материальные точки покоятся. Это возможно, если сумма сил, действующих на каждую материальную точку, равна нулю:
Введем понятие виртуального перемещения. Виртуальное перемещение — это мысленное бесконечно малое перемещение, которое в данный момент времени материальная точка может совершить, не нарушая связей. Чтобы отличать виртуальные перемещения от реальных перемещений материальных точек, будем обозначать их греческой буквой Домножая равенства (2.6) на Первое слагаемое в (2.7) представляет работу активных сил на виртуальных перемещениях. Это — работа, которую совершили бы активные силы, если бы эти перемещения произошли. Ее называют виртуальной работой активных сил. Соответственно второе слагаемое в (2.7) дает виртуальную работу сил реакции связей. Существует большое количество связей, для которых виртуальная работа сил реакции связей равна нулю. Такие связи называются идеальными связями. Идеальными являются связи, осуществляемые нерастяжимыми нитями и в пренебрежении сил трения связи, обеспечиваемые твердыми телами. Для идеальных связей второе слагаемое в равенстве (2.7) равно нулю. В результате получаем уравнение В отличие от равенства (2.7), которое вследствие выполнения условий равновесия (2.6) представляет собой тождество, выражение (2.8) является уравнением. Так как при наличии связей не все Принцип виртуальных перемещений является основным принципом, применяемым в решении задач статики в механике. Проведенные для статики рассуждения обобщаются и на случай динамики. Для этого необходимо в уравнении (2.5) перенести Если формально ввести силы инерции
Уравнение (2.10) формулируется как принцип Даламбера: Работа активных сил вместе с силами инерции на виртуальных перемещениях равна нулю. Принцип Даламбера является основным принципом динамики систем материальных точек со связями. В отсутствие связей все Виртуальные перемещения
Подставляя выражения для Поскольку вариации обобщенных координат
В системе уравнений (2.13) нет сил реакции связей, и число уравнений равно числу степеней свободы. В дальнейшем во все уравнения будут входить только активные силы, и мы специально не будем отмечать это.
Принцип Гамильтона Использование принципа Даламбера позволяет не учитывать силы реакции связей и дает возможность применять произвольные обобщенные координаты. Однако, получение уравнений в обобщенных координатах может представлять трудности из-за наличия в принципе Даламбера Рассмотрим случай, когда силы имеют потенциал. Тогда виртуальная работа сил запишется в форме В общем случае потенциальная энергия может зависеть от времени. Поскольку вариация вычисляется при фиксированном
По аналогии с выражениями (1.12) частные производные от потенциальной энергии по обобщенным координатам называют обобщенными силами:
Для того чтобы преобразовать слагаемые с ускорениями к вариации от скалярной функции, предварительно проинтегрируем уравнение В сумме, содержащей ускорения, рассмотрим одно слагаемое, например
Будем считать, что начальное в момент времени
Такие же преобразования можно произвести для всех координат всех материальных точек. Учтем еще выражение (2.14) виртуальной работы через потенциальную функцию. В результате для интеграла (2.17) получим
Время может и не входить в функцию Лагранжа. Интеграл из (2.20) обозначается буквой После введения этих обозначений условие (2.20) принимает вид Вариация действия равна нулю. Это означает, что действие имеет экстремум, принимает наибольшее или наименьшее значение, если в интеграл (2.22) в качестве зависимости Теперь можно сформулировать интегральный принцип, называемый принципом Гамильтона: Движение механической системы за конечный промежуток времени от Для консервативных систем принцип Гамильтона эквивалентен законам Ньютона. Поэтому он может считаться основным принципом механики, из которого выводятся все уравнения механики.. Это — вариационный принцип, так как зависимость обобщенных координат от времени
8. Получение уравнений Лагранжа из принципа Гамильтона. Из принципа Гамильтона обычным методом вариационного исчисления можно получить дифференциальные уравнения. Наряду с зависимостью
Это уже было отмечено ранее, что дифференцирование по времени и варьирование можно переставлять. Вариации координат рассматриваются такими, что в моменты времени Действие для пробных функций Интеграл от одного из слагаемых первой суммы в (3.5) вычислим по частям:
Согласно условию (3.4), на пределах интегрирования
Поскольку вариации координат Несмотря на то, что функция Лагранжа равна разности кинетической и потенциальной энергии, в выборе функции Лагранжа имеется некоторый произвол. Две функции Лагранжа, отличающиеся на полную производную по времени от произвольной функции координат и времени, дают одни и те же уравнения движения. Покажем это. Пусть Тогда для разности действий, отвечающих этим функциям Лагранжа, получим:
Вследствие того, что вариация координат на пределах интегрирования Ур-ия Лагранжа обобщаются на механические системы, в которых действуют непотенциальные силы. Выражение для; обо6щенной непотенциалыюй силы нужно добавить в правую часть уравнений Лагранжа. Они тогда принимают вид В частном случае, когда непотенциальные силы являются силами трения, пропорциональными первой степени скорости, они могyт быть получены из диссипативной функции Рэлея:
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 868; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.013 с.) |

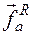 наряду с действующими, или активными силами
наряду с действующими, или активными силами  записывают в правую часть уравнений второго закона Ньютона:
записывают в правую часть уравнений второго закона Ньютона: 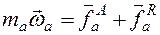 (2.5)
(2.5) (2.6)
(2.6) , то есть виртуальное перемещение материальной точки с индексом
, то есть виртуальное перемещение материальной точки с индексом  обозначим
обозначим  , а реальное бесконечно малое ее перемещение по-прежнему будет обозначаться как
, а реальное бесконечно малое ее перемещение по-прежнему будет обозначаться как 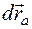 .
. и суммируя по всем материальным точкам системы, получим
и суммируя по всем материальным точкам системы, получим  (2.7)
(2.7)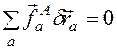 (2.8)
(2.8) . Эти условия по-прежнему выполняются в отсутствие связей, когда
. Эти условия по-прежнему выполняются в отсутствие связей, когда  направо и проделать те же операции, что и в статике. В результате получается уравнение:
направо и проделать те же операции, что и в статике. В результате получается уравнение:  (2.9)
(2.9) , то его можно записать в таком же виде, как уравнение принципа виртуальных перемещений:
, то его можно записать в таком же виде, как уравнение принципа виртуальных перемещений: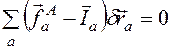 . (2.10)
. (2.10) . Эти бесконечно малые изменения обобщенных координат рассматриваются для фиксированного момента времени и называются вариациями обобщенных координат. Посчитаем дифференциал от выражений (2.2 Преобразование от декартовых координат к обобщенным координатам в векторной форме:
. Эти бесконечно малые изменения обобщенных координат рассматриваются для фиксированного момента времени и называются вариациями обобщенных координат. Посчитаем дифференциал от выражений (2.2 Преобразование от декартовых координат к обобщенным координатам в векторной форме:  ) при фиксированном
) при фиксированном  . Так как время фиксировано и любое изменение обобщенных координат приводит к изменению
. Так как время фиксировано и любое изменение обобщенных координат приводит к изменению  , совместимых со связями, то полученные бесконечно малые изменения
, совместимых со связями, то полученные бесконечно малые изменения  (2.11)
(2.11) . (2.12)
. (2.12) (2.13)
(2.13) (2.14)
(2.14) (2.15)
(2.15) (2.16)
(2.16) . (2.17)
. (2.17) . Индекс
. Индекс  (2.18)
(2.18) и конечное в момент времени
и конечное в момент времени  положения системы материальных точек заданы. Поэтому
положения системы материальных точек заданы. Поэтому  для этих моментов времени равно нулю, и первое слагаемое в (2.18) обращается в нуль. Так как вариации координат рассматриваются для фиксированных моментов времени, то производную по времени и варьирование можно переставить местами. Второе слагаемое в (2.18) преобразуется к виду
для этих моментов времени равно нулю, и первое слагаемое в (2.18) обращается в нуль. Так как вариации координат рассматриваются для фиксированных моментов времени, то производную по времени и варьирование можно переставить местами. Второе слагаемое в (2.18) преобразуется к виду (2.19)
(2.19) . (2.20) Разность кинетической и потенциальной энергии, которая входит в последний из интегралов в формуле (2.20), называется функцией Лагранжа и обозначается буквой
. (2.20) Разность кинетической и потенциальной энергии, которая входит в последний из интегралов в формуле (2.20), называется функцией Лагранжа и обозначается буквой  . Функция Лагранжа зависит от координат и скоростей материальных точек. При переходе к обобщенным координатам она выражается через обобщенные координаты и обобщенные скорости:
. Функция Лагранжа зависит от координат и скоростей материальных точек. При переходе к обобщенным координатам она выражается через обобщенные координаты и обобщенные скорости: (2.21)
(2.21) и называется действием;
и называется действием;  (2.22)
(2.22) . (2.23)
. (2.23) подставить функции, описывающие движение механической системы. Поэтому условие экстремума действия можно использовать для отыскания закона движения системы материальных точек.
подставить функции, описывающие движение механической системы. Поэтому условие экстремума действия можно использовать для отыскания закона движения системы материальных точек. , отличающиеся от
, отличающиеся от  (3.1) Дифференцируя равенство (3.1) по времени, найдем
(3.1) Дифференцируя равенство (3.1) по времени, найдем  (3.2) Откуда следует, что вариация скорости равна производной от вариации координаты:
(3.2) Откуда следует, что вариация скорости равна производной от вариации координаты:  . (3.3).
. (3.3). (3.4)
(3.4) разложим в ряд в линейном приближении по
разложим в ряд в линейном приближении по  , и
, и  :
:  (3.5)
(3.5) (3.6)
(3.6) . Поэтому первое слагаемое в последнем равенстве обращается в нуль. Подставляя теперь результат из (3.6) в (3.5) и записывая вариацию действия, получим
. Поэтому первое слагаемое в последнем равенстве обращается в нуль. Подставляя теперь результат из (3.6) в (3.5) и записывая вариацию действия, получим (3.7)
(3.7) . В результате получается система дифференциальных уравнений, которые в механике называются уравнениями Лагранжа:
. В результате получается система дифференциальных уравнений, которые в механике называются уравнениями Лагранжа: 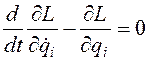 (3.8) Уравнения Лагранжа - это система дифференциальных уравнений относительно неизвестных обобщенных координат
(3.8) Уравнения Лагранжа - это система дифференциальных уравнений относительно неизвестных обобщенных координат  отличаются на полную производную по времени от некоторой функции
отличаются на полную производную по времени от некоторой функции  ;
; 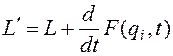 (3.9)
(3.9)
 равны. Поэтому онибудут обращаться в нуль одними и теми же зависимостями
равны. Поэтому онибудут обращаться в нуль одними и теми же зависимостями 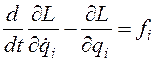 , где
, где  (3,10)
(3,10) ;
;  (3.11) Коэффициенты
(3.11) Коэффициенты  могут зависеть от координат и характеризуют силы трения в механической системе. Для механических систем, в которых силы трения могут быть описаны диссипативной функцией Рэлея, уравнения Лагранжа имеют вид
могут зависеть от координат и характеризуют силы трения в механической системе. Для механических систем, в которых силы трения могут быть описаны диссипативной функцией Рэлея, уравнения Лагранжа имеют вид  (3.12) Ур-ия (3.10) и (3.12) не могут быть получены на основе вариационного принципа. Они выводятся непосредственно из принципа Даламбера. В лагранжевом формализме можно включать в уравнения движения силы немеханической природы. Например, ур-ия движения заряда
(3.12) Ур-ия (3.10) и (3.12) не могут быть получены на основе вариационного принципа. Они выводятся непосредственно из принципа Даламбера. В лагранжевом формализме можно включать в уравнения движения силы немеханической природы. Например, ур-ия движения заряда  в электромагнитном поле получаются из фунции Лагранжа, которая содержит слагаемые, описывающие взаимодействие заряда с полем:
в электромагнитном поле получаются из фунции Лагранжа, которая содержит слагаемые, описывающие взаимодействие заряда с полем:  (3.13) где
(3.13) где  и
и  — скалярный и векторный потенциалы электромагнитного поля,
— скалярный и векторный потенциалы электромагнитного поля,  — скорость света в вакууме. Электромагнитные величины записаны в гауссовой системе единиц. При замене функции Лагранжа классической механики на функцию Лагранжа специальной теории относительности ур-ия Лагранжа дают ур-ия движения механики спец. теории относительности.
— скорость света в вакууме. Электромагнитные величины записаны в гауссовой системе единиц. При замене функции Лагранжа классической механики на функцию Лагранжа специальной теории относительности ур-ия Лагранжа дают ур-ия движения механики спец. теории относительности.


