
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виртуальные (возможные) перемещения голономных системСодержание книги
Поиск на нашем сайте
Связи и их классификация Свободная материальная точка Несвободная материальная точка Свободная материальная система Несвободная материальная система Связь – все то, что ограничивает перемещение системы в пространстве.
В зависимости от уравнения (1) существуют связи: 1. Удерживающая связь f=0 (описывается уравнением) Неудерживающая связь f<0(описывается неравенством)
2. Нестационарная, реономная связь (связь зависит от времени)
3. Кинематическая связь
Голономная связь:
1) Интегрированная (голономная) 2) Неинтегрированная (неголомная)
4. Силеронная (стационарная) Время не входит
Виртуальные (возможные) перемещения голономных систем Голономные системы – системы, в которых встречаются только голономные связи.
При некотором
С точностью до первого порядка малости, уравнение (1) говорит, что точка М будет находиться на поверхности связи. Виртуальным перемещением точки наз. такое малое перемещение мысленно осуществляемое из данного положения при фиксированном времени t, которое с точностью до членов первого порядка малости включительно не нарушат связи.
Идеальные связи Идеальные связи – связи, работа которых на виртуальном перемещении системы равна нулю.
Если силу трения перевести в активные силы, т.е.
Обобщенные координаты; число степеней свободы системы. Обобщенные координаты S = 3n – h (n-кол-во матер. точек, h-число голономн. связей) Число степеней свободы
У свободного тела шесть степеней свободы.
Действительное и возможное перемещения при стационарных и нестационарных связях
Если в уравнение связи время не входит явно, то такая связь называется стационарной (склерономной):
Если в уравнение связи время входит явно, то такая связь называется нестационарной (реономная):
При стационарных связях действительное перемещение совпадает с одним из возможных перемещений. При нестационарной связи действительное перемещение может не совпадать ни с одним из возможных перемещений. Виртуальные перемещения - возможные перемещения материальных точек системы, допускаемые мгновенно (в момент t) связями, из одной точки по разным траекториям в один и тот же момент времени.
Действительное перемещение материальных точек системы есть возможное перемещение, определяемое связями и уравнениями движения
а возможное перемещение только от связей.
Устойчивость состояний равновесия: теорема Лагранжа – Дирихле, принцип Торичелли, теорема Ляпунова По Ляпунову: Устойчивое состояние равновесия системы такое, когда при малом начальном отклонении системы все ее точки будут двигаться не уходя от положения равновесия далее наперед заданного расстояния. Теорема Лагранжа – Дирихле: При устойчивом равновесии системы ее потенциальная энергия принимает миним. значение Ограничения: 1) Силы потенциальны 2) Связи голономны, идеальны, стационарны Принцип Торичелли: При устойчивом равновесии системы ее центр тяжести занимает наинизшее положение. Ограничения: 1) Силы – силы тяжести 2) Связи идеальны, голономны, стационарны Теорема Ляпунова: Равновесие системы неустойчиво, если отсутствие минимума потенциальной энергии системы обнаруживается уже по членам второго порядка в разложении
Обобщенные силы К понятию обобщенные силы приводят преобразование элементарной работы сил и выражают через обобщенные координаты. Три способа вычисления обобщенных сил: 1. На основе (1):
2. Задается
Множитель Q при изменении обобщенной координаты В выражении для виртуальной работы активных сил системы наз. обобщенной силой, соответствующей начальной координате 3. Для потенциальных сил.
Обобщенная сила в консервативной системе равна частичной производной потенциальной энергии по соответствующей обобщенной координате, взятой с обратным знаком. Условия равновесия в обобщенных координатах. Согласно принципу возможных перемещений
Одно вариационное выражение (2) эквивалентно «S» алгебраическим уравнениям (3). Для равновесия голономных систем необходимо и достаточно, чтобы все вариационные системы были равны нулю. Частный случай: для потенциальных сил:
Общее уравнение динамики
Уравнение (1) запишем в виде:
При движении механической системы с идеальными связями работа всех активных сил и сил инерции на любом возможном перемещении системы равна нулю.
Уравнение Лагранжа II рода Из формулы
Связи идеальные:
Силы только потенциальны:
Обыкновенное однородное ДУ 2-го порядка (с нулевой правой частью):
Число уравнения равно числу степеней свободы.
Виртуальная работа Виртуальная работа – работа сил на виртуальных перемещениях системы Пусть система материальных точек занимает в некоторый момент времени t какое-то положение. Обозначим через Fk силы, приложенные к точкам системы. Из данного положения при фиксированном времени t, сообщим системе виртуальное перемещение δrk. Будем считать, что на этом перемещении силы Fk, приложенные к системе, не изменяются. Составим сумму работ этих сил на вирт. перемещении δrk
14. Интеграл движения: обобщенный интеграл движения f Интеграл системы уравнений
Системы уравнений (1) может иметь не более “2S” – первых интегралов. Первые интегралы уравнений Лагранжа II-го рода бывают 2-х видов: 1)Обобщенные интегралы энергии. 2)Циклический интеграл.
Допущение:
Консервативная система – система, которая обладает обычным интегралом энергии. Из (2) сумма отбрасывается: первый интеграл получается из (2):
Задача Циолковского
S- площадь сопла, p(x)- давление атмосферное, р- давление газа. Из (1): Ракета летит в пустоте:
Из (2):
Формула Циолковского Пренебрежем влиянием силы тяготения. Из
Пусть
Н. у. t=0,
Связи и их классификация Свободная материальная точка Несвободная материальная точка Свободная материальная система Несвободная материальная система Связь – все то, что ограничивает перемещение системы в пространстве.
В зависимости от уравнения (1) существуют связи: 1. Удерживающая связь f=0 (описывается уравнением) Неудерживающая связь f<0(описывается неравенством)
2. Нестационарная, реономная связь (связь зависит от времени)
3. Кинематическая связь
Голономная связь:
1) Интегрированная (голономная) 2) Неинтегрированная (неголомная)
4. Силеронная (стационарная) Время не входит
Виртуальные (возможные) перемещения голономных систем Голономные системы – системы, в которых встречаются только голономные связи.
При некотором
С точностью до первого порядка малости, уравнение (1) говорит, что точка М будет находиться на поверхности связи. Виртуальным перемещением точки наз. такое малое перемещение мысленно осуществляемое из данного положения при фиксированном времени t, которое с точностью до членов первого порядка малости включительно не нарушат связи.
Идеальные связи Идеальные связи – связи, работа которых на виртуальном перемещении системы равна нулю.
Если силу трения перевести в активные силы, т.е.
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.150 (0.009 с.) |

 (1)
(1)









 :
:


 (1)
(1) или
или  , при выполнении этих условий связь идеальна.Rk-равнодействующая реакции связей
, при выполнении этих условий связь идеальна.Rk-равнодействующая реакции связей , то и поверхность с трением будет идеальной связью.
, то и поверхность с трением будет идеальной связью. – это S независимых параметров любой размерности, однозначно определяющих положение системы в пространстве.
– это S независимых параметров любой размерности, однозначно определяющих положение системы в пространстве. - это число независимых вариаций координат
- это число независимых вариаций координат  , однозначно определяющих положение системы в пространстве.
, однозначно определяющих положение системы в пространстве. (m – число неголомных связей)
(m – число неголомных связей) - возможное (виртуальное) перемещение – малое, мысленное перемещение, допускаемое связями с точностью до величин первого порядка малости.
- возможное (виртуальное) перемещение – малое, мысленное перемещение, допускаемое связями с точностью до величин первого порядка малости.

 , u=1,2,…,n; i=1,2,…,n
, u=1,2,…,n; i=1,2,…,n зависит только от связей.
зависит только от связей.
 зависит от связей и от сил.
зависит от связей и от сил. в ряд Тейлора
в ряд Тейлора



 (1)
(1)


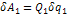





 .
. (2)
(2)
 ,
,  Т.к.
Т.к.  , то
, то 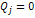 (3)
(3)


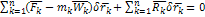
 (1) – общее уравнение динамики
(1) – общее уравнение динамики
 - общее уравнение динамики – принцип Доломбера - Лагранжа:
- общее уравнение динамики – принцип Доломбера - Лагранжа: :
:






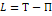 (кинетический потенциал, функция Лагранжа)
(кинетический потенциал, функция Лагранжа) 


 “2S”
“2S”


 (где С - константа)
(где С - константа) (1), или интегралом движения, или первым интегралом, если при подстановке вместо
(1), или интегралом движения, или первым интегралом, если при подстановке вместо  решений системы (1), функция f обращается в константу.
решений системы (1), функция f обращается в константу.






 L от времени не зависит
L от времени не зависит
 (2) - обобщенный интеграл энергии или интеграл Якоби
(2) - обобщенный интеграл энергии или интеграл Якоби


 - обычный интеграл
- обычный интеграл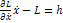







 (1)
(1) - реактивная сила
- реактивная сила -расчет тяги
-расчет тяги
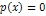
 (2)
(2)


 - эффективная скорость истечения
- эффективная скорость истечения

 - силы тяготения
- силы тяготения

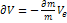

 – эффективная скорость истечения
– эффективная скорость истечения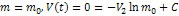


 - формула Циолковского
- формула Циолковского - число Циолковского
- число Циолковского - стартовый вес ракеты
- стартовый вес ракеты
 - формула Циолковского
- формула Циолковского


