
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия в обобщенных координатахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для нестационарных связей радиус – вектор
В общем случае кинетическую энергию материальной системы можно представить суммой квадратичной
Для стационарных связей:
Одна степень свободы:
Две степени свободы:
Уравнение Лагранжа II рода Из формулы
Связи идеальные:
Силы только потенциальны:
Обыкновенное однородное ДУ 2-го порядка (с нулевой правой частью):
Число уравнения равно числу степеней свободы.
Виртуальная работа Виртуальная работа – работа сил на виртуальных перемещениях системы Пусть система материальных точек занимает в некоторый момент времени t какое-то положение. Обозначим через Fk силы, приложенные к точкам системы. Из данного положения при фиксированном времени t, сообщим системе виртуальное перемещение δrk. Будем считать, что на этом перемещении силы Fk, приложенные к системе, не изменяются. Составим сумму работ этих сил на вирт. перемещении δrk
14. Интеграл движения: обобщенный интеграл движения f Интеграл системы уравнений
Системы уравнений (1) может иметь не более “2S” – первых интегралов. Первые интегралы уравнений Лагранжа II-го рода бывают 2-х видов: 1)Обобщенные интегралы энергии. 2)Циклический интеграл.
Допущение:
Консервативная система – система, которая обладает обычным интегралом энергии. Из (2) сумма отбрасывается: первый интеграл получается из (2):
Принцип возможных перемещений При равновесии механической системы с идеальными связями, виртуальная работа всех активных сил равна нулю.
В положении равновесия все обобщенные силы равны нулю Теорема: Для того чтобы система материальных точек, подчиненная идеальным стационарным, голономным и удерживающим связям, находилась в равновесии, необходимо и достаточно, чтобы работа всех активных сил на любом виртуальном перемещении системы и скорости всех точек в начальный момент времени равнялись нулю.
15. Интеграл движения: циклические интегралы f Интеграл системы уравнений
Системы уравнений (1) может иметь не более “2S” – первых интегралов. Первые интегралы уравнений Лагранжа II-го рода бывают 2-х видов: 1)Обобщенные интегралы энергии. 2)Циклический интеграл.
Позиционные координаты – обобщенные координаты, которые явно входят в функцию Лагранжа. Из (1) для циклической координаты:
Канонические переменные. Функция Гамильтона Если ввести “S” новых переменных
характеристическая функция механической системы, выраженная через канонические переменные: обобщенные координаты Можно показать, что
Для стационарных задач (допущение):
допущение (частный случай):
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.105.110 (0.005 с.) |

 зависит от всех обобщенных координат и времени t.
зависит от всех обобщенных координат и времени t. ;
;  ;
; 
 (1)
(1) i=1,2,…,s
i=1,2,…,s


 В пустых скобках выражение (1)
В пустых скобках выражение (1)




 , линейной
, линейной  и нулевой
и нулевой  форм относительно обобщенных скоростей.
форм относительно обобщенных скоростей.












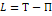 (кинетический потенциал, функция Лагранжа)
(кинетический потенциал, функция Лагранжа) 


 “2S”
“2S”


 (где С - константа)
(где С - константа) (1), или интегралом движения, или первым интегралом, если при подстановке вместо
(1), или интегралом движения, или первым интегралом, если при подстановке вместо  решений системы (1), функция f обращается в константу.
решений системы (1), функция f обращается в константу.





 L от времени не зависит
L от времени не зависит
 (2) - обобщенный интеграл энергии или интеграл Якоби
(2) - обобщенный интеграл энергии или интеграл Якоби


 - обычный интеграл
- обычный интеграл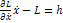







 - Система будет находиться в равновесии.
- Система будет находиться в равновесии.


 Циклическая координата – обобщенная координата, которая не входит в функцию Лагранжа, но входит явно в соответствующая ей обобщенная скорость
Циклическая координата – обобщенная координата, которая не входит в функцию Лагранжа, но входит явно в соответствующая ей обобщенная скорость
 - циклическая координата
- циклическая координата

 - циклическинтеграл
- циклическинтеграл и предположить, что эти зависимости могут быть разрешены относительно обобщенных скоростей
и предположить, что эти зависимости могут быть разрешены относительно обобщенных скоростей  , то система уравнений
, то система уравнений  - форма Лагранжа;
- форма Лагранжа;  - переменные Лагранжа.
- переменные Лагранжа.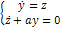 - форма Гамильтона; y, z – переменные Гамильтона
- форма Гамильтона; y, z – переменные Гамильтона - “2S” переменные Гамильтона
- “2S” переменные Гамильтона


 - функция Гамильтона -- это
- функция Гамильтона -- это и обобщенные импульсы
и обобщенные импульсы 
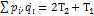 , тогда функция Гамильтона
, тогда функция Гамильтона 
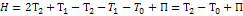
 ,
,  - Совпадает с обобщенным интегралом энергии.
- Совпадает с обобщенным интегралом энергии.


