
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция Лагранжа в обобщенных координатахСодержание книги
Поиск на нашем сайте Для того чтобы записать функцию Лагранжа в обобщенных координатах, необходимо пересчитать к ним потенциальную и кинетическую энергию механической системы. Если потенциальная энергия задана как функция декартовых координат, то, заменяя их на обобщенные с помощью преобразования [от декартовых координат к обобщенным координатам в векторной форме: (2.2), получим потенциальную энергию как функцию обобщенных координат
Введем матрицу коэффициентов, зависящих только от обобщенных координат:
Матрица
Если формулы преобразования к обобщенным координатам не содержат времени, то кинетическая энергия является однородной функцией второго порядка от обобщенных скоростей. Функция Лагранжа (разность кинетической и потенциальной энергии называется функцией Лагранжа и обозначается буквой
Если формулы преобразования к обобщенным координатам содержат время, то выражение для кинетической энергии в обобщенных координатах будет содержать члены, линейные по обобщенным скоростям, и члены, не зависящие от обобщенных скоростей.
Обобщенный импульс, обобщенная энергия Циклические координаты. Для одной материальной точки производные от функции Лагранжа по
В обобщенных координатах вводится понятие обобщенного импуль са. Обобщенный импульс, сопряженный координате Если координаты не декартовы, то обобщенные импульсы больше не равны проекциям импульса. Их можно выразить через импульсы отдельных материальных точек, составляющих систему материальных точек. Рассмотрим функцию Лагранжа как сложную функцию обобщенных координат и обобщенных скоростей:
Вычислим производные по обобщенным координатам как производные от сложной функции:
Для частных производных от векторов скорости из формулы (2.4) находим, что
В рез-те имеем следующую связь обобщенного импульса с импульсами отдельных материальных точек механической системы: Обобщенный импульс, сопряженный декартовой координате, равен проекции импульса на декартову oсь. Обобщенный импульс, сопряженный угловой координате, равен проекции момента импульса на ось вращения. Чтобы убедиться в этом, выразим радиус-вектор материальной точки через сферические координаты:
Используя представление (3.32), легко проверить,
Подставляя выражение (3.33) в формулу (3.31), найдем для одной материальной точки то есть обобщенный импульс Используя определение обобщенного импульса, уравнения Лагранжа можно записать в форме Возможны случаи, когда некоторые координаты не входят в функцию Лагранжа, но в ней присутствуют их производные по времени — обобщенные скорости. Такие координаты называются циклическими координатами. Например, если в функции Лагранжа материальной точки (массой
Так как обобщенный импульс, сопряженный циклической координате, остается постоянным при движении механической системы, то говорят, что он сохраняется. Каждой циклической координате отвечает свой закон сохранения. Наличие законов сохранения упрощает решение задач механики. Уравнения Лагранжа — это дифференциальные уравнения второго порядка относительно неизвестных координат Обобщенная энергия Найдем полную производную от функции Лагранжа по времени. Так как функция Лагранжа зависит от обобщенных координат и обобщенных скоростей, которые сами являются функциями времени, то получим выражение
Воспользуемся формулой Лейбница для дифференцирования произведения двух функций и получим из нее следующее равенство:
С помощью этого равенств преобразуем выражение (3.37) и запишем его в форме
Сумма в правой части выражения (3.38) равна нулю вследствие выполнения уравнений Лагранжа
Равенство (3.38) дает полную производную от обобщенной энергии по времени
Если функция Лагранжа не зависит явно oт времени, то правая часть в формуле (3.40) равна нулю и обобщенная энергия сохраняется при движении механической системы. Для обычных механических систем при условии, что формулы преобразования к обобщенным координатам не содержат времени, функция Лагранжа дается формулой (3.26). Найдем в этом случае обобщенную энергию. Для обобщенных импульсов получим
Подставляя этот результат в формулу (3.39), найдем
то есть определение обобщенной энергии в этом случае совпадает с обычным определением механической энергии. Если на механическую систему действую силы, не имеющие потенциала, то в правой части уравнений Лагранжа стоит уже не нуль. Поэтому сумма в правой части формулы (3.38) не равна нулю, и механическая энергия не будет сохраняться даже при отсутствии явной зависимости от времени в функции Лагранжа. В частности, если непотенциальные силы являются силами трения, описываемыми диссипативной функцией Рэлея, то уменьшение механической энергии дается формулой Формула (3.43) получается из соотношения (3.38) при подстановке в него уравнения (3.12). Для механических систем, в которых силы трения могут быть описаны диссипативной функцией Рэлея, уравнения Лагранжа имеют вид
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1649; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 (2.2) ]
(2.2) ] . Выражение для кинетической энергии мы найдем только для случая, когда связи стационарны и формулы преобразования (2.2) не содержат времени. Подставляя формулу для скорости [
. Выражение для кинетической энергии мы найдем только для случая, когда связи стационарны и формулы преобразования (2.2) не содержат времени. Подставляя формулу для скорости [  (2.4)] из (2.4) в выражение для кинетической энергии (
(2.4)] из (2.4) в выражение для кинетической энергии ( ), имеем
), имеем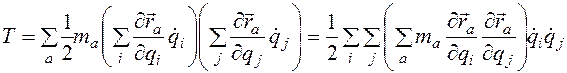 (3.23)
(3.23) (3.24)
(3.24) — это симметричная матрица. Учитывая обозначения (3.24), запишем кинетическую энергию механической системы в виде
— это симметричная матрица. Учитывая обозначения (3.24), запишем кинетическую энергию механической системы в виде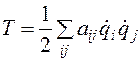 (3.25)
(3.25) ) принимает форму
) принимает форму (3.26)
(3.26) равны проекциям импульса на декартовы оси
равны проекциям импульса на декартовы оси ;
;  ;
;  (3.27)
(3.27) определяется по формуле, аналогичной формулам (3.27):
определяется по формуле, аналогичной формулам (3.27):  (3.28)
(3.28)
 (3.29)
(3.29)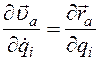 (3.30)
(3.30) (3.31)
(3.31) (3.32)
(3.32) (3.33)
(3.33)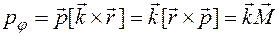 , (3.34)
, (3.34) , сопряженный угловой координате
, сопряженный угловой координате  , равен проекции момента импульса на ось OZ, которая в данном случае представляет ось вращения при изменении угла
, равен проекции момента импульса на ось OZ, которая в данном случае представляет ось вращения при изменении угла 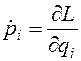 (3.35)
(3.35) , находящейся в потенциальном поле
, находящейся в потенциальном поле  :
:  (3.14) потенциальная энергия не будет зависеть от координат х и у, то координаты х и у будут циклическими. Для циклической координаты правая часть уравнения (3.35) равна нулю и, следовательно, интеграл этого уравнения имеет вид
(3.14) потенциальная энергия не будет зависеть от координат х и у, то координаты х и у будут циклическими. Для циклической координаты правая часть уравнения (3.35) равна нулю и, следовательно, интеграл этого уравнения имеет вид . (3.36)
. (3.36) . Соотношения вида (3.36) являются дифференциальными уравнениями первого порядка относительно
. Соотношения вида (3.36) являются дифференциальными уравнениями первого порядка относительно  (3.37)
(3.37)

 (3.38)
(3.38)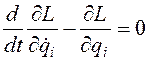 (3.8). Выражение в скобках в левой части формулы (3.38), взятое с обратным знаком, называется обобщенной энергией. Обозначим его буквой
(3.8). Выражение в скобках в левой части формулы (3.38), взятое с обратным знаком, называется обобщенной энергией. Обозначим его буквой  :
: (3.39).
(3.39). (3.40)
(3.40) (3.41)
(3.41) (3.42)
(3.42) (3.43)
(3.43) (3.12)
(3.12)


