
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача двух тел. Приведенная массаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим задачу о движении двух взаимодействующих только между собой материальных точек. Вследствие однородности и изотропности пространства потенциальная энергия взаимодействия может зависеть только от расстояния между точками. Функция Лагранжа для данной задачи запишется в форме
Рассматриваемая система материальных точек замкнута. Поэтому ее импульс сохраняется, и система отсчета центра инерции является инерциальной системой отсчета. Задачу будем решать в системе отсчета центра инерции. Начало координат поместим в центр инерции, что дает
Введем радиус-вектор
С помощью формул (4.2) и (4.3) выразим векторы
Потенциальная энергия теперь зависит только от величины вектора
Выраженная через радиус-вектор
Функция Лагранжа (4.6) — это функция Лагранжа одной материальной точки массы
Масса Если масса одной материальной точки, например Поскольку масса Солнца намного больше массы каждой из планет Солнечной системы, то в первом приближении можно пренебречь взаимодействием планет между собой и движением Солнца вокруг центра инерции Солнечной системы. В этом приближении движение отдельной планеты рассматривается как движение материальной точки в поле тяготения Солнца. Учет взаимодействия планет между собой приводит к задаче многих тел, взаимодействующих между собой. Эта задача не может быть сведена к квадратурам и решается приближенными методами.
Движение в центральном поле Вследствие сферической симметрии поля сохраняется вектор момента импульса
Координата
Согласно формуле (3.34) обобщенный импульс для одной материальной точки
Этот обобщенный импульс равен проекции момента импульса материальной точки на ось OZ. Будем считать, что постоянная М положительна, что соответствует выбору положительного направления оси OZ по положительному направлению вектора момента импульса. В этом случае всегда
Из формул (4.9) и (4.10) находим скорость изменения площади с течением времени. Эта величина называется секторной скоростью и в центральном поле
За равные промежутки времени радиус-вектор материальной точки заметает одинаковые площади. Это утверждение, известное как закон площадей, является другой формулировкой закона сохранения момента импульса. Закон площадей выполняется для любого центрального поля. Так как функция Лагранжа материальной точки в центральном поле не зависит явно от времени, то сохраняется энергия материальной точки. В полярных координатах выражение для энергии записывается в форме
Из выражения (4.9) найдем производную
где введено понятие эффективной потенциальной энергии
Формула (4.13) для энергии совпадает с формулой для энергии материальной точки, движущейся по радиусу и находящейся в потенциальном поле с эффективной потенциальной энергией
Разделяя в выражении (4.15) переменные и интегрируя его, получим неявную зависимость
Выражение (4.15) и интеграл (4.16) имеют смысл только тогда, когда подкоренное выражение не отрицательно, то есть когда выполняется неравенство Найдем теперь уравнение траектории. Так как производные
Интегрируя выражение (4.17), находим уравнение траектории в полярных координатах:
Интеграл можно вычислить только после задания потенциальной энергии
Рис. 4.3 Рис. 4.4 Примеры возможных траекторий приведены на рис. 4.3 и рис. 4.4. Угол
Если при сложении нескольких
где Задача Кеплера Рассмотрим важный случай центрального поля, когда потенциальная энергия равна Ур-ие траектории получим, вычисляя интеграл (4.18). Запишем его для поля притяжения, выбирая знак минус в (4.21). Положим также постоянную
где введены две новые постоянные: параметр
Материальная точка, движущаяся по гиперболе, может уйти на бесконечность и будет иметь там ненулевую скорость. При
Размер большой полуоси эллипса не зависит от момента импульса материальной точки и определяется только ее энергией. Период обращения материальной точки вокруг центра найдем путем интегрирования соотношения (4.11) закона площадей. За период обращения вокруг центра площадь, заметаемая радиусом-вектором материальной точки, равна площади эллипса. Используя значения для
Для планет Солнечной системы отношение Закон 1. Планета движется по эллипсу, в одном из фокусов которого находится Солнце. Закон 2. Площади, заметаемые радиусом-вектором планеты за одинаковые промежутки времени, равны. Закон 3. Квадраты периодов обращения планет относятся как кубы их больших полуосей. Уравнение траектории для поля отталкивания, когда
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1003; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.009 с.) |

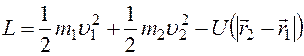 (4.1)
(4.1) (4.2)
(4.2) , направленный от первой материальной точки ко второй:
, направленный от первой материальной точки ко второй: (4.3)
(4.3) и
и  через вектор
через вектор  ;
;  (4.4)
(4.4) и
и  через вектор
через вектор  , кинетическую энергию системы двух материальных точек можно записать как кинетическую энергию одной материальной точки массой
, кинетическую энергию системы двух материальных точек можно записать как кинетическую энергию одной материальной точки массой (4.5)
(4.5) (4.6)
(4.6) , движущейся в потенциальном поле, зависящем только от расстояния до начала координат. Такое потенциальное поле называется центральным полем. Сила, действующая в центральном поле на материальную точку, направлена по прямой, соединяющей материальную точку с центром поля:
, движущейся в потенциальном поле, зависящем только от расстояния до начала координат. Такое потенциальное поле называется центральным полем. Сила, действующая в центральном поле на материальную точку, направлена по прямой, соединяющей материальную точку с центром поля: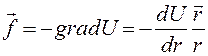 (4.7)
(4.7) , много больше массы другой материальной точки, то из формул (4.4) и (4.5) получим, что приближенно
, много больше массы другой материальной точки, то из формул (4.4) и (4.5) получим, что приближенно  ,
, 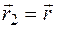 ,
, 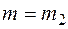 , то есть центр инерции системы двух тел совпадает с более массивным телом, а приведенная масса равна массе менее массивного тела. В этом случае задача двух тел сводится к задаче о движении одного тела в потенциальном поле, создаваемом другим телом.
, то есть центр инерции системы двух тел совпадает с более массивным телом, а приведенная масса равна массе менее массивного тела. В этом случае задача двух тел сводится к задаче о движении одного тела в потенциальном поле, создаваемом другим телом. , определенный относительно центра поля. Так как
, определенный относительно центра поля. Так как  , то векторы
, то векторы  перпендикулярны постоянному вектору
перпендикулярны постоянному вектору  (4.8)
(4.8) является циклической. Сопряженный ей обобщенный импульс сохраняется:
является циклической. Сопряженный ей обобщенный импульс сохраняется: (4.9)
(4.9)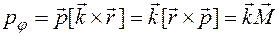 , (3.34)
, (3.34)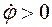 и, следовательно, материальная точка в центральном поле движется так, что угол
и, следовательно, материальная точка в центральном поле движется так, что угол  Закон сохранения (4.9) часто формулируется как закон площадей. Рассмотрим два положения материальной точки на траектории в два бесконечно близких момента времени, как показано на рис. 4.1. Из рисунка видно, что площадь бесконечно малого сектора, ограниченного двумя положениями радиуса-вектора и участком траектории, равна
Закон сохранения (4.9) часто формулируется как закон площадей. Рассмотрим два положения материальной точки на траектории в два бесконечно близких момента времени, как показано на рис. 4.1. Из рисунка видно, что площадь бесконечно малого сектора, ограниченного двумя положениями радиуса-вектора и участком траектории, равна . (4.10)
. (4.10) (4.11)
(4.11) (4.12)
(4.12) и подставим ее в формулу (4.12). В результате получим
и подставим ее в формулу (4.12). В результате получим (4.13)
(4.13) , равной
, равной (4.14)
(4.14) . Из соотношения (4.13) находим, что
. Из соотношения (4.13) находим, что (4.15)
(4.15) :
:
 (4.16)
(4.16) ). Исследование этого неравенства позволяет, не вычисляя интеграла, определить области пространства, в которых возможно движение материальной точки при заданных энергии
). Исследование этого неравенства позволяет, не вычисляя интеграла, определить области пространства, в которых возможно движение материальной точки при заданных энергии  и моменте импульса
и моменте импульса  . Качественно такое исследование можно провести графическим путем, если построить график зависимости
. Качественно такое исследование можно провести графическим путем, если построить график зависимости  . Пример такого построения приведен на рис.. На этом графике условия неравенства
. Пример такого построения приведен на рис.. На этом графике условия неравенства  . Следовательно, при обращении вокруг центра поля материальная точка будет то приближаться к центру на расстояние
. Следовательно, при обращении вокруг центра поля материальная точка будет то приближаться к центру на расстояние  , то удаляться от него на расстояние
, то удаляться от него на расстояние  .
. и
и  (4.17)
(4.17) (4.18)
(4.18) . Если положить
. Если положить  , то изменение знака
, то изменение знака  и где, следовательно, материальная точка находится на минимальном или максимальном удалении от центра поля. Точки минимального или максимального удаления материальной точки от центра поля называются точками поворота. Таким образом при
и где, следовательно, материальная точка находится на минимальном или максимальном удалении от центра поля. Точки минимального или максимального удаления материальной точки от центра поля называются точками поворота. Таким образом при  начало отсчета угла
начало отсчета угла  , лежащим по разные стороны от точки поворота, отвечают одинаковые абсолютные значения угла
, лежащим по разные стороны от точки поворота, отвечают одинаковые абсолютные значения угла  и
и  .
.

 между положениями
между положениями  (4.19)
(4.19) , то материальная точка возвратится на уже пройденный участок траектории и сама траектория будет замкнутой кривой. Условие замкнутости траектории записывается в форме
, то материальная точка возвратится на уже пройденный участок траектории и сама траектория будет замкнутой кривой. Условие замкнутости траектории записывается в форме (4.20)
(4.20) — целые числа. Если это условие не выполняется, то траектория будет незамкнутой кривой, расположенной в кольце между окружностями с радиусами
— целые числа. Если это условие не выполняется, то траектория будет незамкнутой кривой, расположенной в кольце между окружностями с радиусами  (4.21) Силу, действующую на материальную точку, найдем по формуле
(4.21) Силу, действующую на материальную точку, найдем по формуле 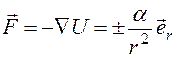 (4,22), где
(4,22), где  — единичный вектор, направленный по радиусу. Знак плюс относится к полю отталкивания, когда сила направлена от центра. Знак минус - полю притяжения. Для рассматриваемого потенциального поля сила обратно пропорциональна квадрату радиуса. Такую зависимость силы от расстояния имеют поле тяготения сферически симметричной массы и электрическое поле точечн. или сферически симметричн. заряда.
— единичный вектор, направленный по радиусу. Знак плюс относится к полю отталкивания, когда сила направлена от центра. Знак минус - полю притяжения. Для рассматриваемого потенциального поля сила обратно пропорциональна квадрату радиуса. Такую зависимость силы от расстояния имеют поле тяготения сферически симметричной массы и электрическое поле точечн. или сферически симметричн. заряда. =0 и выберем знак плюс перед интегралом. Такой выбор постоянной и знака перед интегралом соответствует выбору оси ОХ в направлении на положение минимального удаления материальной точки от центра. Тогда интеграл имеет вид
=0 и выберем знак плюс перед интегралом. Такой выбор постоянной и знака перед интегралом соответствует выбору оси ОХ в направлении на положение минимального удаления материальной точки от центра. Тогда интеграл имеет вид (4.23) Интеграл (4.23) приводится к табличному интегралу путем замены
(4.23) Интеграл (4.23) приводится к табличному интегралу путем замены  и выделением полного квадрата под знаком корня. Результат интегрирования можно записать в форме
и выделением полного квадрата под знаком корня. Результат интегрирования можно записать в форме  (4.24)
(4.24) и эксцентриситет
и эксцентриситет  . Они равны:
. Они равны: ;
;  (4.25) Уравнение (4.24) задает в полярных координатах одно из конических сечений: гиперболу, параболу или эллипс. Начало полярной системы координат совпадает с одним из фокусов гиперболы или эллипса или с фокусом параболы. Вид конического сечения зависит от величины эксцентриситета
(4.25) Уравнение (4.24) задает в полярных координатах одно из конических сечений: гиперболу, параболу или эллипс. Начало полярной системы координат совпадает с одним из фокусов гиперболы или эллипса или с фокусом параболы. Вид конического сечения зависит от величины эксцентриситета  уравнение задает гиперболу. В этом случае положительна энергия материальной точки:
уравнение задает гиперболу. В этом случае положительна энергия материальной точки:  (4.26)
(4.26) второе слагаемое в (4.26) обращается в 0 и энергия материальной точки равна ее кинетической энергии
второе слагаемое в (4.26) обращается в 0 и энергия материальной точки равна ее кинетической энергии  . Если
. Если  , то эксцентриситет
, то эксцентриситет  и уравнение (4.24) задает параболу. Материальная точка по-прежнему может уйти на бесконечность, но скорость ее на бесконечности =0. И наконец, при отрицательной энергии
и уравнение (4.24) задает параболу. Материальная точка по-прежнему может уйти на бесконечность, но скорость ее на бесконечности =0. И наконец, при отрицательной энергии  . Тогда уравнение (4.24) описывает эллипс. Движение материальной точки ограничено областью вблизи центра поля.
. Тогда уравнение (4.24) описывает эллипс. Движение материальной точки ограничено областью вблизи центра поля. Если пренебречь взаимодействием планет между собой, то полученные для поля притяжения с
Если пренебречь взаимодействием планет между собой, то полученные для поля притяжения с  результаты можно применить к описанию движения планет Солнечной системы. Так как масса Солнца
результаты можно применить к описанию движения планет Солнечной системы. Так как масса Солнца  >> массы планет Солнечной системы, то центр поля можно считать совпадающим с центром Солнца, а приведенную массу считать = массе планеты. Из з-на всемирного тяготения имеем
>> массы планет Солнечной системы, то центр поля можно считать совпадающим с центром Солнца, а приведенную массу считать = массе планеты. Из з-на всемирного тяготения имеем  . Выразим измеряемые астрономами величины — большую полуось орбиты и период обращения планеты — через энергию и момент импульса планеты. Из рис. 4.5 траектории планеты видно, что
. Выразим измеряемые астрономами величины — большую полуось орбиты и период обращения планеты — через энергию и момент импульса планеты. Из рис. 4.5 траектории планеты видно, что ;
;  (4.27)
(4.27) и
и  из (4.27), формулу
из (4.27), формулу  для площади эллипса и закон площадей (4.11), получим
для площади эллипса и закон площадей (4.11), получим (4.28) Подставляя в (4.28) значения
(4.28) Подставляя в (4.28) значения 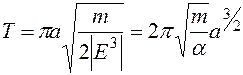 (4.29)
(4.29)

 . Lля них период обращения зависит только от величины большой полуоси орбиты. Эти рез-ты для движения материальной точки по эллипсу в центральном поле в приложении к движению планет Солнечной системы открыты Кеплером. Законы Кеплера
. Lля них период обращения зависит только от величины большой полуоси орбиты. Эти рез-ты для движения материальной точки по эллипсу в центральном поле в приложении к движению планет Солнечной системы открыты Кеплером. Законы Кеплера .:
.:  (4.30)
(4.30)  и
и 


