
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные одномерные колебанияСодержание книги
Поиск на нашем сайте
Рассмотрим одномерную механическую систему, то есть механическую систему с одной степенью свободы. Функция Лагранжа произвольной механической системы в обобщенных координатах дается формулой Пусть в положении Мы предполагаем, что вторая производная Разложим функции
В разложении для потенциальной энергии уже учтены условия (5.2) и обозначения (5.3). В выражении для кинетической энергии введено обозначение Ценность полученного результата заключается в том, что функция Лагранжа любой одномерной механической системы, удовлетворяющей сформулированным выше условиям, в данном приближении имеет вид (5.5). Индивидуальность механической системы проявляется только в значениях постоянных Если в механической системе присутствует трение, то считается, что его можно описать при помощи диссипативной функции Рэлея:
Запишем уравнения Лагранжа с диссипативной функцией в приближении малых колебаний. Для одномерной системы уравнение Лагранжа имеет вид
Подставляя в (5.7) функцию Лагранжа (5.5) и диссипативную функцию (5.6), приходим к дифференциальному уравнению
Разделим это уравнение на
В результате получим линейное дифференциальное уравнение второго порядка с постоянными коэффициентами, описывающее малые свободные одномерные колебания при наличии трения:
Решение ур-ия (5.10) ищем в форме Если
Здесь Общее решение можно записать в двух формах:
Переход от одной формы к другой осуществляется простыми тригонометрическими преобразованиями. Два набора постоянных связаны соотношениями: В отсутствие трения, когда
Решение (5.17) описывает свободные малые колебания около положения равновесия. Величина Частота определяется свойствами механической сисгемы и не зависит от начальных условий. Амплитуда колебаний
Уравнение малых колебаний часто удобно представлять в комплексной форме. Так как комплексное число
то решение (5.17) дается его действительной частью:
Если над комплексными величинами производятся только линейные операции (сложение, вычитание, умножение на действительные величины, дифференцирование и интегрирование), то действия с действительной и комплексной частями комплексного числа производятся независимо. В то же время иметь экспоненты в формулах удобнее, если выполняются операции дифференцирования или интегрирования, так как при этих операциях экспонента не меняет своего вида. Поэтому во всех расчетах, где производятся только линейные операции, косинусы можно заменить на экспоненты, опуская знак реальной части. Тогда в конце вычислений из полученного в комплексной форме результата необходимо взять только его действительную часть. При наличии трения уравнения (5.15) описывают колебания, амплитуда которых уменьшается по экспоненциальному закону. Такие колебания называются затухающими колебаниями. Скорость убывания амплитуды определяется показателем
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.164 (0.006 с.) |

 . В одномерном случае суммация в ней отсутствует. Поэтому индексы можно опустить. В результате функция Лагранжа запишется:
. В одномерном случае суммация в ней отсутствует. Поэтому индексы можно опустить. В результате функция Лагранжа запишется:  (5.1)
(5.1)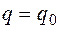 система имеет положение устойчивого равновесия. В этом положении потенциальная энергия механической системы минимальна. Условие мин.потенциальной энергии:
система имеет положение устойчивого равновесия. В этом положении потенциальная энергия механической системы минимальна. Условие мин.потенциальной энергии:  ;
;  (5.2)
(5.2)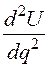 , обозначенная здесь буквой
, обозначенная здесь буквой 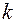 , в положении равновесия отлична от нуля. Если она =0, то колебания становятся нелинейными, или ангармоническими. Введем новую обобщенную координату
, в положении равновесия отлична от нуля. Если она =0, то колебания становятся нелинейными, или ангармоническими. Введем новую обобщенную координату 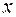 — отклонение от положения равновесия:
— отклонение от положения равновесия:  ,
,  (5.3)
(5.3) и
и  в ряд вблизи положения равновесия и, считая эти отклонения малыми, ограничимся в разложении нулевым приближением для
в ряд вблизи положения равновесия и, считая эти отклонения малыми, ограничимся в разложении нулевым приближением для  ;
;  (5.4)
(5.4)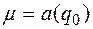 и вследствие того, что обобщенная скорость также мала, в разложении
и вследствие того, что обобщенная скорость также мала, в разложении  не сказывается на уравнениях движения. Поэтому положим ее =0. С точностью до членов второго порядка малости функция Лагранжа записывается в форме
не сказывается на уравнениях движения. Поэтому положим ее =0. С точностью до членов второго порядка малости функция Лагранжа записывается в форме  . (5.5)
. (5.5)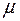 и
и  ;
;  В диссипативной функции рассматривается такое же приближение, как и в кинетической энергии. В принятом приближении для диссипативной функции имеем
В диссипативной функции рассматривается такое же приближение, как и в кинетической энергии. В принятом приближении для диссипативной функции имеем ;
;  (5.6)
(5.6) (5.7)
(5.7) (5.8)
(5.8) ;
;  (5.9)
(5.9)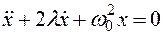 (5.10)
(5.10) . Характеристическое уравнение имеет корни:
. Характеристическое уравнение имеет корни:  ;
;  . (5.11)
. (5.11)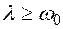 , что отвечает сильному трению, то решение уравнения (5,10) записывается в экспоненциальной форме:
, что отвечает сильному трению, то решение уравнения (5,10) записывается в экспоненциальной форме: , для
, для  (5.12)
(5.12) , для
, для  (5.13)
(5.13) — произвольные постоянные. В обоих случаях абсолютная величина смещения х монотонно убывает с ростом времени, и, следовательно, механическая система приближается к положению равновесия, не совершая колебаний. Если
— произвольные постоянные. В обоих случаях абсолютная величина смещения х монотонно убывает с ростом времени, и, следовательно, механическая система приближается к положению равновесия, не совершая колебаний. Если  , что означает слабое трение, то решение уравнения (5.10) записывается через тригонометрические функции. Введем обозначение
, что означает слабое трение, то решение уравнения (5.10) записывается через тригонометрические функции. Введем обозначение  (5.14)
(5.14)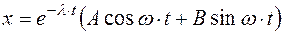 ,
,  (5.15)
(5.15)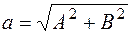 ,
,  (5.16)
(5.16)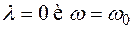 , решение имеет вид
, решение имеет вид ,
,  (5-17)
(5-17) называется частотой колебаний.
называется частотой колебаний. и начальная фаза
и начальная фаза  определяются начальными условиями. Энергия системы, совершающей колебания в отсуютвие трения, сохраняется и пропорциональна квадрату амплитуды:
определяются начальными условиями. Энергия системы, совершающей колебания в отсуютвие трения, сохраняется и пропорциональна квадрату амплитуды: (5.18)
(5.18) , где
, где  — комплексная амплитуда
— комплексная амплитуда 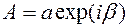 , по формулам Эйлера записывается в виде
, по формулам Эйлера записывается в виде (5.19)
(5.19) (5.20)
(5.20) . Как видно из формулы (5,14), трение также уменьшает частоту колебаний.
. Как видно из формулы (5,14), трение также уменьшает частоту колебаний.


