
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные многомерные колебанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обобщенные координаты положения равновесия механической системы с несколькими степенями свободы обозначим через
Как и в одномерном случае, потенциальную энергию механической системы разложим в ряд до членов второго порядка малости:
Здесь Коэффициенты
Матрица Запишем функцию Лагранжа многомерной механической системы в приближении малых колебаний. Постоянную Зависимость функции Лагранжа (5.43) oт обобщенных координат Чтобы записать уравнения Лагранжа для функции Лагранжа (5.43), вычислим производные от нее по
Уравнения Лагранжа (5.45) представляют собой однородную систему линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. Решение их ищется в форме где
Так как система уравнений (5.47) — однородная система, то она имеет отличные от нуля решения для дает уравнение для нахождения постоянной Поэтому уравнение (5.48) будет алгебраическим уравнением степени Для каждой частоты Подставим два вектора с различными номерами
Домножая первое из них на
Если следующие алгебраические условия, которым удовлетворяют векторы
Двойную сумму в (5.51) можно рассматривать как определение скалярного произведения в линейном пространстве векторов Из (5.52) видно, что при положительно определенной матрице Так как система дифференциальных уравнений (5.45) — однородная система, то ее общее решение дается суммой частных решений, домноженных на произвольные постоянные: Решение (5.54) записано в комплексной форме. Представим Зависимость каждой координаты от времени задается в виде конечной суммы гармонических колебаний. В эту сумму входят только колебания с собственными частотами. Амплитуды Обозначим Выражения (5.56) можно рассматривать как формулы преобразования от координат
Функция Лагранжа (5.59) имеет наиболее простой вид. Координаты Очевидно, что решение уравнений (5.60) для каждой нормальной координаты - это одномерное гармоническое колебание Преобразование (5.56) к нормальным координатам было проведено нами после решения системы дифференциальных уравнений, описывающих малые колебания. Как правило, нормальные координаты не являются координатами каких-либо частей механической системы, а представляют собой расчетные величины. Однако можно задать такие начальные данные, когда все координаты механической системы будут изменяться по гармоническому закону с одной из нормальных частот. Для этого начальные данные нужно выбрать так, чтобы амплитуды всех нормальных колебаний, кроме одной, были равны нулю. Тогда в суммах (5.55) останется только по одному слагаемому, которое и будет определять частоту малых колебаний для всех координат.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.216.224 (0.009 с.) |

 . Для смещений из положения равновесия и обобщенных скоростей имеем
. Для смещений из положения равновесия и обобщенных скоростей имеем ;
;  (5.39)
(5.39) (5.40)
(5.40) — число степеней свободы. При записи формулы (5.40) учтено, что вследствие минимума потенциальной энергии в положении равновесия первые производные от нее =0, и введено обозначение
— число степеней свободы. При записи формулы (5.40) учтено, что вследствие минимума потенциальной энергии в положении равновесия первые производные от нее =0, и введено обозначение  (5.41)
(5.41) постоянны и, как следует из их определения (5 41), симметричны по индексам i,j. To есть они задают симметричную постоянную матрицу. Так как по определению
постоянны и, как следует из их определения (5 41), симметричны по индексам i,j. To есть они задают симметричную постоянную матрицу. Так как по определению  есть минимальное значение потенциальной энергии, то двойная сумма в разложении (5.40) должна быть положительной при любых значениях
есть минимальное значение потенциальной энергии, то двойная сумма в разложении (5.40) должна быть положительной при любых значениях  . Матрицы, для которых такая сумма всегда положительна, называются положительно определенными. Таким образом, матрица
. Матрицы, для которых такая сумма всегда положительна, называются положительно определенными. Таким образом, матрица 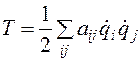 зависящие в общем случае от координат коэффициенты
зависящие в общем случае от координат коэффициенты  также разлагаем в ряд вблизи положения равновесия. Поскольку обобщенные скорости
также разлагаем в ряд вблизи положения равновесия. Поскольку обобщенные скорости  , считаются малыми, то в разложении можно ограничиться нулевым приближением:
, считаются малыми, то в разложении можно ограничиться нулевым приближением: ;
;  (5.42)
(5.42) — это также симметричная матрица постоянных коэффициентов. Поскольку кинетическая энергия всегда положительна, то матрица
— это также симметричная матрица постоянных коэффициентов. Поскольку кинетическая энергия всегда положительна, то матрица  (5.43)
(5.43) и
и  . Эти производные равны
. Эти производные равны ;
;  (5-44) Ограничимся только уравнениями Лагранжа в отсутствие трения. Подстановка в уравнения Лагранжа частных производных из (5.44) дает
(5-44) Ограничимся только уравнениями Лагранжа в отсутствие трения. Подстановка в уравнения Лагранжа частных производных из (5.44) дает  (5.45)
(5.45) (5.46)
(5.46) и
и  — постоянные, которые необходимо найти. При подстановке
— постоянные, которые необходимо найти. При подстановке  из (5.46) в уравнения Лагранжа (5.45) получим характеристическую систему линейных однородных алгебраических уравнений относительно постоянных
из (5.46) в уравнения Лагранжа (5.45) получим характеристическую систему линейных однородных алгебраических уравнений относительно постоянных  (5.47)
(5.47) (5.48)
(5.48) . Такое уравнение имеет
. Такое уравнение имеет  . Греческий индекс для обозначения номера решения введен специально для того, чтобы отличать номер решения от номера координаты. Корни
. Греческий индекс для обозначения номера решения введен специально для того, чтобы отличать номер решения от номера координаты. Корни  являются действительными числами. Они определяют частоты колебаний, которые могут происходить в механической системе, и называются собственными частотами.
являются действительными числами. Они определяют частоты колебаний, которые могут происходить в механической системе, и называются собственными частотами. — можно рассматривать как вектор в
— можно рассматривать как вектор в 
 и
и  в систему уравнений (5.47) и запишем вытекающие оттуда соотношения:
в систему уравнений (5.47) и запишем вытекающие оттуда соотношения: ;
;  (5.49)
(5.49) , а второе на
, а второе на  , суммируя еще по индексу i и вычитая одно из другого, получим результат:
, суммируя еще по индексу i и вычитая одно из другого, получим результат: (5.50)
(5.50) , то двойная сумма в (5.50) равна нулю. Для кратных корней, когда
, то двойная сумма в (5.50) равна нулю. Для кратных корней, когда  и
и  ,, в линейном подпространстве решений можно всегда подобрать векторы, для которых двойная сумма также обратится в нуль. Наконец, для одинаковых векторов
,, в линейном подпространстве решений можно всегда подобрать векторы, для которых двойная сумма также обратится в нуль. Наконец, для одинаковых векторов  двойная сумма не определена. Вследствие положительной определенности матрицы
двойная сумма не определена. Вследствие положительной определенности матрицы  она положительна. Можно потребовать, чтобы эта сумма равнялась единице. В результате получим
она положительна. Можно потребовать, чтобы эта сумма равнялась единице. В результате получим :
: ;
;  (5.51)
(5.51) . При выполнении условий (5.51) из уравнений (5.47) получим
. При выполнении условий (5.51) из уравнений (5.47) получим  (5.52)
(5.52)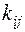 квадраты частот
квадраты частот  будут положительными. Подставляя полученные решения для
будут положительными. Подставляя полученные решения для  (5.53)
(5.53) (5.54)
(5.54) в виде
в виде  и перейдем к действит. записи
и перейдем к действит. записи  (5.55)
(5.55) и начальные фазы
и начальные фазы  определяются начальными условиями. Коэффициенты
определяются начальными условиями. Коэффициенты  отдельные колебания, входящие в сумму (5.55). Тогда решение (5.55) запишется в форме
отдельные колебания, входящие в сумму (5.55). Тогда решение (5.55) запишется в форме  (5.56)
(5.56) к координатам
к координатам  (5.57)
(5.57) (5.58)
(5.58) (5.59)
(5.59) также называются нормальными частотами. Уравнения Лагранжа для каждой из нормальных координат имеют вид уравнений одномерных свободных колебаний:
также называются нормальными частотами. Уравнения Лагранжа для каждой из нормальных координат имеют вид уравнений одномерных свободных колебаний:  (5.60)
(5.60) (5.61)
(5.61)


