
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонические колебания и их характеристики
Вопросы ко второй контрольной по физике. Гармонические колебания и их характеристики Колебательный процесс – повторяющееся во времени движение или процесс. Колебаниями называются процессы, при которых какая-либо физическая величина принимает многократно, через равные (или почти равные) последовательные промежутки времени, одни и те же (или приблизительно одни и те же) значения. Природа этой физической величины может быть самой различной. Все колебания характеризуются периодом—промежутком времени, через который значения колеблющейся величины начинают повторяться, амплитудой — наибольшим отклонением от нулевого значения. Механическими колебаниями называются такие колебания, для которых изменяющейся физической величиной является отклонение материальной точки (или системы материальных точек) от положения равновесия. Гармоническими колебаниями называются колебания, при которых изменение физической величины X с течением времени (закон колебаний) выражается формулой: X = Acos(wt +j) Здесь X является функцией времени, т.е. X = X(t). Множитель A – амплитуда. Величина w называется круговой (или угловой) частотой. Круговая частота w связана с периодом колебаний T и с обычной частотой n (числом колебаний в единицу времени) соотношениями: ω=2*π/T=2*π*n Частота n измеряется в герцах [1 Гц = 1 колебанию в секунду]. Величина wt + j -фаза колебаний. Фаза измеряется в угловых единицах, т.е. в градусах или радианах (долях p). С помощью фазы можно характеризовать отклонение колеблющейся величины от нулевого значения в заданный момент времени t. Про величины, колеблющиеся с одинаковой частотой, одновременно достигающие наибольших значений, одновременно проходящие нулевые значения и изменяющиеся в любой момент времени в одну и ту же сторону, говорят, что они колеблются в одинаковых фазах. Если же величины одновременно достигают максимальных значений, одновременно проходят нулевые значения, но изменяются в любой момент времени в противоположные стороны, то про них говорят, что они колеблются в противофазах. Найдем первую и вторую производные по времени от величины x, совершающей гармонические колебания: X=Acos(ω0t) X’=-Aωsinωt, где Aω-максимальная амплитуда скорости.
X’’=-Aω2cos(ω0t), где Aω2 –максимальная амплитуда ускорения. Уравнение гармонических колебаний:x’’+(k/m)*x=0 значит ω2=sqrt(k/m) и T=2π*sqrt (m/k) Дифференциальное уравнение гармонических колебаний x’’+ω02x=0 Свободные гармонические колебания без затуханий, с затуханиями. Дифференциальные уравнения, описывающие их решения. Колебания, которые происходят в системе, выведенной каким- либо способом из положения равновесия и предоставленной затем самой себе, называются собственными или свободными колебаниямисистемы. Гармонические колебания могут происходить не только под действием упругой силы, но также под действием силы любого происхождения, лишь бы она была пропорциональна отклонению системы от положения равновесия. Чтобы в системе существовали свободные незатухающие колебания необходимо, чтобы при выведении системы из положения равновесия возникали силы, стремящиеся вернуть тело в равновесие. Положение равновесия бывает устойчивое, неустойчивое и безразличное. Если у нас есть пружина, на которую подвесили груз, то она удлинится на величину kx0, тогда уравнение движения пружинного маятника примет вид mg- kx0- kx=mx’ and mx’’+kx=0. *Далее взять уравнение гармонических колебаний и все по первому вопросу. Если на колеблющееся тело, помимо упругих сил, действуют достаточно большие силы трения, то происходит заметное затухание колебаний: амплитуда каждого последующего колебания становится меньше амплитуды предыдущего.
F(упругости)=-kx F(трения)=-rV Mx’’=-kx-rv X’’=-(k/m)x-(r/m)x’=0 X’’+(k/m)x+(2r/2m)x’=0 (β=r/2m-коэффициент затухания) X’’+2βx’+ω02x=0 – уравнение затухающих гармонических колебаний. X=Aexp(-βt)cosωt Так как β<<ω0, то ω примерно равно ω0 Энергия. X=Acosωt V=-Aω0sin ω0t Eп=(kx2)/2 Ek+ Eп=(kA2)/2 Резонанс. Вынужденные колебания возникают в системе под действием внешней силы, изменяющейся по периодическому закону. Колебания, которые происходят в системе под действием периодически изменяющейся силы, называются вынужденными колебаниями. Как показывает опыт, частота вынужденных колебаний совпадает с частотой вынуждающей силы. В качестве примера системы, совершающей вынужденные колебания, рассмотрим колебания груза массы, подвешенного на пружине с коэффициентом жесткости. Будем предполагать, что на груз действует вынуждающая сила, изменяющаяся по периодическому закону:
F=F0cosΩt X’’+2βx’+ω0x= f0cosΩt f0=F0/m x=A0 cosΩt. Если Ω= ω0, то происходит резкий рост амплитуды (резонанс). В случае жидкого трения, при котором сила пропорциональна скорости тела, величина затухания характеризуется декрементом затухания. Декремент затухания показывает, во сколько раз предыдущая амплитуда An больше последующей An+1, то есть Δ= An / An+1. Часто также употребляется логарифмический декремент затухания δ= lnΔ. Логарифмический декремент затухания, вообще говоря, связан с коэффициентом b силы трения, действующей на колеблющееся тело b=(2mδ)/T. Вопросы ко второй контрольной по физике. Гармонические колебания и их характеристики Колебательный процесс – повторяющееся во времени движение или процесс. Колебаниями называются процессы, при которых какая-либо физическая величина принимает многократно, через равные (или почти равные) последовательные промежутки времени, одни и те же (или приблизительно одни и те же) значения. Природа этой физической величины может быть самой различной. Все колебания характеризуются периодом—промежутком времени, через который значения колеблющейся величины начинают повторяться, амплитудой — наибольшим отклонением от нулевого значения. Механическими колебаниями называются такие колебания, для которых изменяющейся физической величиной является отклонение материальной точки (или системы материальных точек) от положения равновесия. Гармоническими колебаниями называются колебания, при которых изменение физической величины X с течением времени (закон колебаний) выражается формулой: X = Acos(wt +j) Здесь X является функцией времени, т.е. X = X(t). Множитель A – амплитуда. Величина w называется круговой (или угловой) частотой. Круговая частота w связана с периодом колебаний T и с обычной частотой n (числом колебаний в единицу времени) соотношениями: ω=2*π/T=2*π*n Частота n измеряется в герцах [1 Гц = 1 колебанию в секунду]. Величина wt + j -фаза колебаний. Фаза измеряется в угловых единицах, т.е. в градусах или радианах (долях p). С помощью фазы можно характеризовать отклонение колеблющейся величины от нулевого значения в заданный момент времени t. Про величины, колеблющиеся с одинаковой частотой, одновременно достигающие наибольших значений, одновременно проходящие нулевые значения и изменяющиеся в любой момент времени в одну и ту же сторону, говорят, что они колеблются в одинаковых фазах. Если же величины одновременно достигают максимальных значений, одновременно проходят нулевые значения, но изменяются в любой момент времени в противоположные стороны, то про них говорят, что они колеблются в противофазах. Найдем первую и вторую производные по времени от величины x, совершающей гармонические колебания: X=Acos(ω0t) X’=-Aωsinωt, где Aω-максимальная амплитуда скорости. X’’=-Aω2cos(ω0t), где Aω2 –максимальная амплитуда ускорения. Уравнение гармонических колебаний:x’’+(k/m)*x=0 значит ω2=sqrt(k/m) и T=2π*sqrt (m/k) Дифференциальное уравнение гармонических колебаний x’’+ω02x=0
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.70.28 (0.009 с.) |
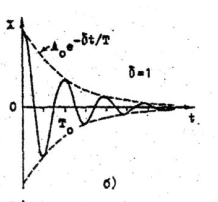 Для изучения колебательного движения при наличии трения обратимся снова к движению груза, подвешенного на пружине. В этом случае во второй закон Ньютона кроме упругой силы F войдет еще сила трения:
Для изучения колебательного движения при наличии трения обратимся снова к движению груза, подвешенного на пружине. В этом случае во второй закон Ньютона кроме упругой силы F войдет еще сила трения:


