
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные одномерные колебанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Часто механические системы, совершающие малые колебания, подвергаются воздействию внешней вынуждающей силы, зависящей от времени. Пусть потенциальная энергия одномерной системы в поле вынуждающей силы равна
где введено обозначение
При подстановке ее в уравнение (5.7) получим уравнение вынужденных колебаний Уравнение (5.23) — это уже неоднородное дифференциальное уравнение. Его решение дается суммой общего решения однородного уравнения (5.10) и частного решения уравнения (5.23): Наиболее интересным случаем вынужденных колебаний является случай, когда внешняя обобщенная сила представляет собой гармоническую функцию
где
В правой части уравнения (5.26) стоит экспонента. Поэтому его частное решение
Представим постоянную
Тогда действительная часть общего решения уравнения(5.23) с гармонической вынуждающей силой (5.25) запишется в виде
В отсутствие трения
Фаза вынужденных колебаний совпадает с фазой вынуждающей силы. Амплитуда вынужденных колебаний растет при Уравнение малых колебаний в случае резонанса принимает вид
При резонансе фаза вынужденных колебаний на
Рассмотрим поведение системы вблизи резонанса, когда частота вынуждающей силы мало отличается от частоты свободных колебаний. Положим, что В выражении (5.33) нужно учитывать только действительную часть, которая равна
Уравнение (5.34) можно интерпретировать как уравнение колебаний с часютой
Если Перейдем к общему случаю, когда присутствует трение
При резонансе, как и в отсутствие трения, колебания отстают от вынуждающей силы на
то есть чем выше добротность, тем меньше полуширина
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.194.5 (0.009 с.) |

 . Разложим ее в ряд вблизи положения равновесия, ограничиваясь приближением первого порядка
. Разложим ее в ряд вблизи положения равновесия, ограничиваясь приближением первого порядка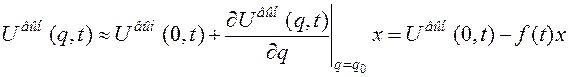 (5.21)
(5.21) для производной от потенциальной энергии по координате, вычисленной в положении равновесия. Слагаемое
для производной от потенциальной энергии по координате, вычисленной в положении равновесия. Слагаемое  не зависит от обобщенных координат и обобщенных скоростей и поэтому не дает вклада в уравнения Лагранжа. Отбросим его и запишем функцию Лагранжа механической системы, находящейся в поле внешней вынуждающей силы:
не зависит от обобщенных координат и обобщенных скоростей и поэтому не дает вклада в уравнения Лагранжа. Отбросим его и запишем функцию Лагранжа механической системы, находящейся в поле внешней вынуждающей силы: (5.22)
(5.22) (5.23)
(5.23) (5.24)
(5.24)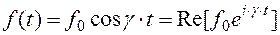 (5.25)
(5.25) — действительная постоянная. Для гармонической вынуждающей силы уравнение (5.23) удобно записать и решать в комплексной форме:
— действительная постоянная. Для гармонической вынуждающей силы уравнение (5.23) удобно записать и решать в комплексной форме: (5.26)
(5.26) также ищем в форме экспоненты
также ищем в форме экспоненты  . Подставляя
. Подставляя  :
: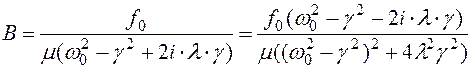 (5.27)
(5.27) , где
, где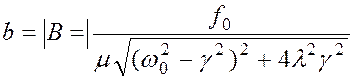 ;
;  (5.28)
(5.28) (5.29)
(5.29) вынужденные колебания (5.29) являются суммой свободных колебаний с частотой
вынужденные колебания (5.29) являются суммой свободных колебаний с частотой 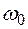 и вынужденных колебаний с частотой вынуждающей силы
и вынужденных колебаний с частотой вынуждающей силы  и амплитудой, зависящей от частоты:
и амплитудой, зависящей от частоты: (5.30)
(5.30) . Если
. Если  , то наступает резонанс и решение (5.30) не имеет смысла. В этом случае частное решение уравнения (5.26) необходимо искать в виде
, то наступает резонанс и решение (5.30) не имеет смысла. В этом случае частное решение уравнения (5.26) необходимо искать в виде  Для постоянной
Для постоянной  (5.31)
(5.31) *. (5.32)
*. (5.32) отличается от фазы вынуждающей силы. Амплитуда вынужденных колебаний монотонно растет с течением времени, и колебания быстро перестают быть малыми.
отличается от фазы вынуждающей силы. Амплитуда вынужденных колебаний монотонно растет с течением времени, и колебания быстро перестают быть малыми. , где
, где  . Выражение (5.30), записанное в комплексной форме, можно привести к виду
. Выражение (5.30), записанное в комплексной форме, можно привести к виду  (5.33)
(5.33) , (5.34) где
, (5.34) где (5.35)
(5.35) и начальная фаза
и начальная фаза  которых медленно меняются с частотой
которых медленно меняются с частотой  . Как видно из (5.35), амплитуда заключена в пределах
. Как видно из (5.35), амплитуда заключена в пределах (5.36)
(5.36) и
и  близки друг к другу, то временами колебания будут почти прекращаться, а после опять возобновляться. Такое поведение системы называют биениями.
близки друг к другу, то временами колебания будут почти прекращаться, а после опять возобновляться. Такое поведение системы называют биениями. При наличии трения первое слагаемое в (5.29) быстро обращается в нуль за счет экспоненциального множителя. В установившемся режиме остается только второе слагаемое. Вынужденные колебания происходят с частотой вынуждающей силы, но отстают от нее по фазе. Начальная фаза вынужденных колебаний, как видно из (5.27) и (5.28), лежит в пределах
При наличии трения первое слагаемое в (5.29) быстро обращается в нуль за счет экспоненциального множителя. В установившемся режиме остается только второе слагаемое. Вынужденные колебания происходят с частотой вынуждающей силы, но отстают от нее по фазе. Начальная фаза вынужденных колебаний, как видно из (5.27) и (5.28), лежит в пределах  . При сильном трении, когда
. При сильном трении, когда  , амплитуда вынужденных колебаний монотонно убывает с ростом частоты вынуждающей силы. Если трение мало, то амплитуда максимальна при резонансной частоте
, амплитуда вынужденных колебаний монотонно убывает с ростом частоты вынуждающей силы. Если трение мало, то амплитуда максимальна при резонансной частоте  .
. Рассмотрим отдельно случай, когда трение очень мало:
Рассмотрим отдельно случай, когда трение очень мало:  . Тогда в первом приближении по
. Тогда в первом приближении по  резонансная частота
резонансная частота  совпадает с частотой
совпадает с частотой  . Вблизи резонанса положим
. Вблизи резонанса положим  . В первом приближении по
. В первом приближении по  ;
;  (5.37)
(5.37) частоту, для которой квадрат амплитуды уменьшается в два раза, то находим, что
частоту, для которой квадрат амплитуды уменьшается в два раза, то находим, что  . Для характеристики систем, совершающих вынужденные колебания, вводится понятие добротности. Добротность — это отношение максимальной амплитуды для резонансной частоты к амплитуде, отвечающей близкой к нулю частоте вынуждающей силы. Используя выражение (5.28) для амплитуды и считая
. Для характеристики систем, совершающих вынужденные колебания, вводится понятие добротности. Добротность — это отношение максимальной амплитуды для резонансной частоты к амплитуде, отвечающей близкой к нулю частоте вынуждающей силы. Используя выражение (5.28) для амплитуды и считая  значение:
значение: (5.38)
(5.38) резонансной кривой и тем выше поднимается ее пик.
резонансной кривой и тем выше поднимается ее пик.


