
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденное комбинационное рассеивание светаСодержание книги
Поиск на нашем сайте
Вынужденное комбинационное рассеяние - это рассеяние света большой интенсивности в нелинейной средепри котором возбуждаются когерентные колебания молекул и рассеянная световая волна имеет частоту ω2, которая меньше частоты падающего света ω1 на частоту молекулярных колебаний. Комбинационное рассеяние – это двухфотонный процесс, в котором один фотон – ω1 (k1) - поглощается и один фотон – ω2 (k2) - излучается; при этом среда переходит из начального состояния |f>, как показано на рис.7.8. из закона сохранения энергии следует что ħ(ω1-ω2)=Еf-Еi≡ħωfi, т.е. разности энергий конечного и начального состояний. Если разность частоты
C классической точки зрения, явление вынужденного комбинационного рассеяния можно трактовать как параметрический процесс, при котором, за счет энергии падающей волны возбуждаются “волна” молекулярных колебаний и световая волна стоксовой частоты. При вынужденном комбинационном рассеянии, кроме стоксовой волны, может возбуждаться антистоксовая волна с частотой: ω1+Ω, а в общем случае могут возбуждаться частоты более высоких порядков: ω1±nΩ, (n =2,3). Вынужденное комбинационное рассеяние возникает лишь при достаточно большой интенсивности падающего света. При малых интенсивностях падающей волны происходит самопроизвольное (спонтанное) комбинационное рассеяние, когда тепловые колебания молекул происходят хаотически. Классическое описание взаимодействия света с внутримолекулярными движениями основывается на учете зависимости электронной поляризуемости молекул α от ядерной конфигурации, задаваемой координатами ядер Qi. В простейшем одномерном случае:
Член
В условиях, когда Q определяется тепловыми движениями в среде, (7.37) описывает спонтанное комбинационное рассеяние. Зависимость α(Q) является одновременно причиной обратного воздействия световых волн на молекулярные колебания. Действительно, энергия взаимодействия молекулы со световой волной выражается с помощью (7.37) в виде: Очевидно, что эта сила может привести к их резонансной ”раскачке”, если поле содержит компоненты с частотами ω1 и ω2, разность которых близка к собственной частоте молекулярных колебаний Ω, т.е. ω1-ω2≈Ω. В этих условиях на хаотическое внутримолекулярное движение, имеющее флуктуационный характер, накладываются регулярные вынужденные колебания. Фазы этих колебаний в различных молекулах определяются фазами компонент светового поля. Вынужденное комбинационное рассеяние является пороговым эффектом, т.е. она возникает, если интенсивность мощной световой волны частоты ω1, падающей на среду, превышает пороговое значение: І1 ≥ Іпор. При этом условии низкочастотная (стоксова) волна с частотой ω2=ω1−Ω экспоненциально усиливается по мере распространения через среду; при І2<< І1 имеем: I2=I20exp(gI1z), (7.39) а коэффициент усиления непосредственно выражается через параметры линии спонтанного рассеивания: где dσ/do – сечение рассеяния, 2Г – ширину линии, N – плотность молекул, g(ω1−ω2) − форм-фактор линии (g(Ω)=1). При gІ1z>>1 исходная волна частоты ω1 истощается, происходит эффективный энергообмен между волнами. Если же говорить о состоянии среды, в которой происходит вынужденное рассеяние, то особенно существенными оказываются два обстоятельства: а) В результате воздействия на среду волны накачки и стоксовой волны происходит фазирование молекулярных колебаний во всем объеме, занятом световыми полями. Процессы фазирования могут быть описаны с помощью классического подхода, основанного на соотношениях типа (7.36)-(7.38). б) Естественно, что при достаточно сильном возбуждении изменяется и разность населенностей между возбуждаемыми колебательными уровнями. Здесь теоретическое описание требует уже квантового подхода; заметим, что выравнивание населенностей приводит к подавлению вынужденного комбинационного рассеяния. В заключение следует отметить, что для возбуждения вынужденного комбинационного рассеяния не нужно каких – либо дополнительных условий, кроме достаточно большой интенсивности лазерного излучения.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 847; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.008 с.) |


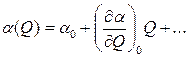 (7.36)
(7.36)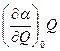 описывает модуляцию света молекулярными колебаниями - в наведенной поляризации молекулы появляются новые частотные компоненты, сдвинутые на частоту колебаний ядер:
описывает модуляцию света молекулярными колебаниями - в наведенной поляризации молекулы появляются новые частотные компоненты, сдвинутые на частоту колебаний ядер: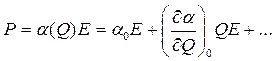 (7.37)
(7.37) , и, следовательно,
, и, следовательно,  в световом поле возникает сила, действующая на молекулярные колебания:
в световом поле возникает сила, действующая на молекулярные колебания:  . (7.38)
. (7.38) , (7.40)
, (7.40)


